北师大版八年级物理 下册 第九章 第2节《滑轮》课件(共33张PPT)
文档属性
| 名称 | 北师大版八年级物理 下册 第九章 第2节《滑轮》课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-08 12:21:26 | ||
图片预览






文档简介
(共34张PPT)
二、滑轮
1.认识定滑轮和动滑轮。
2.知道定滑轮、动滑轮、滑轮组的作用。
3.会根据要求使用和组装滑轮组。
4.了解其他简单机械的一些应用。
教学目标
复习提问:
1. 杠杆的平衡条件?
2.杠杆的应用:
杠杆一般可以分为 杠杆和 杠杆。如右图所示,图一所应用到的是 杠杆,图二所应用到的是 杠杆。
(图一)
(图二)
F1L1=F2L2
省力
费力
省力
费力
新课引入:
上一节课所学的杠杆是一种简单的机械,在这一节里我们将继续学习另一种简单机械。首先,请同学们看一看上图,你能帮助他们解决这个问题吗?
滑轮在使用时,根据轴的位置是否移动,分为定滑轮和动滑轮两种。
使用时,轴固定不动,叫定滑轮。
使用时,轴和重物一起移动,叫动滑轮。
在日常生活中我们经常可以看到定滑轮和动滑轮,同学们能再举出一些例子吗?请说明它们分别是哪一类滑轮。
(图一)定滑轮的应用
(图二)动滑轮的应用
生活中的滑轮
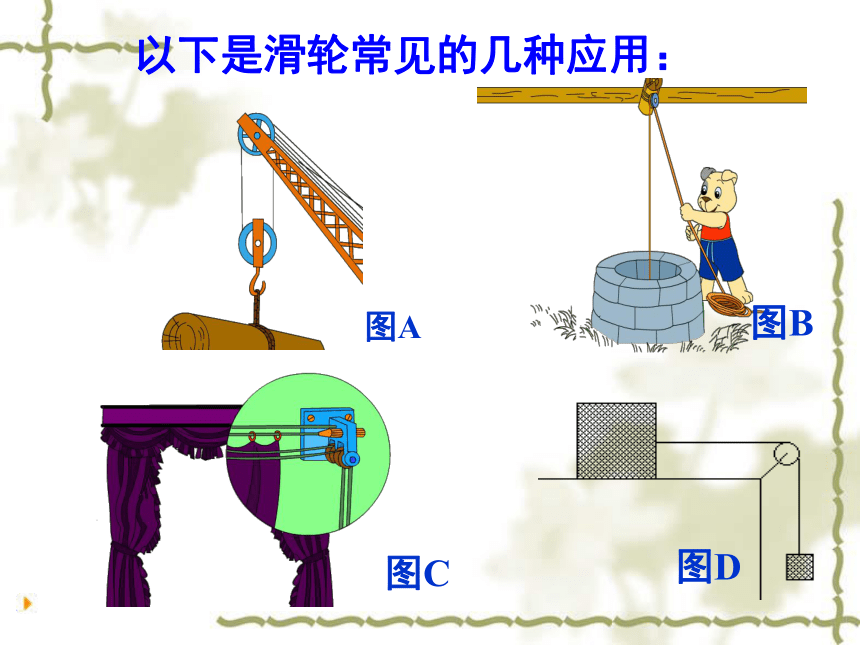
图A
图B
图C
图D
以下是滑轮常见的几种应用:
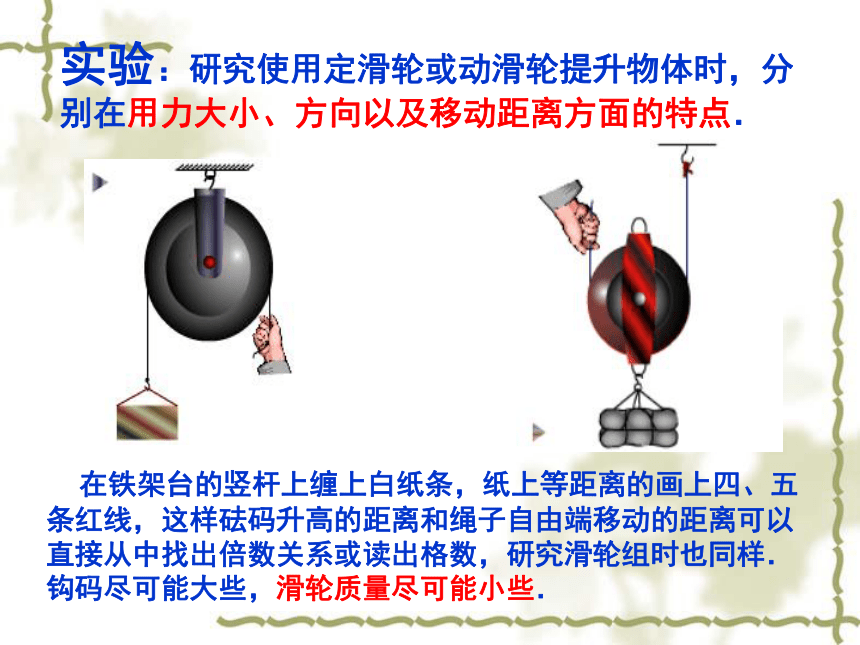
实验:研究使用定滑轮或动滑轮提升物体时,分别在用力大小、方向以及移动距离方面的特点.
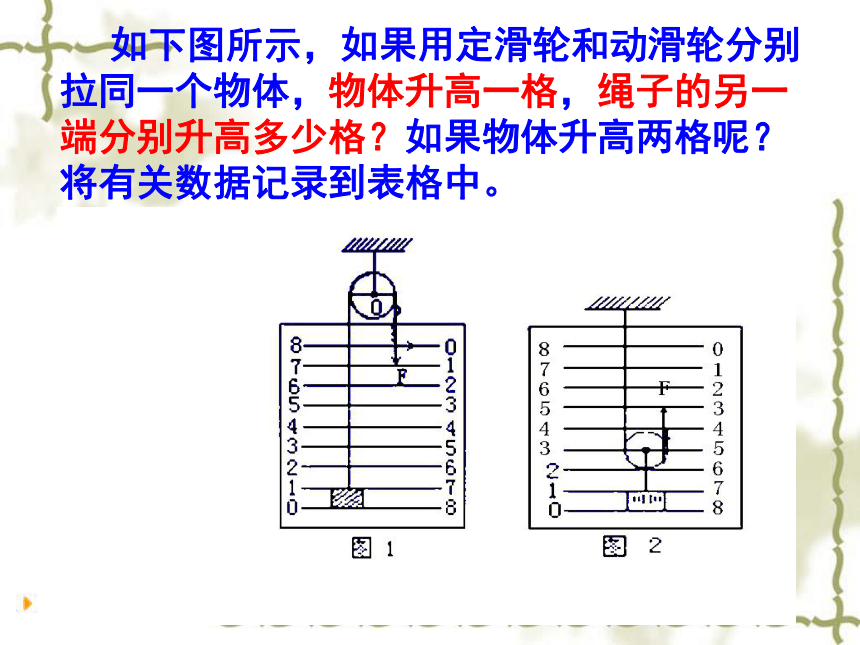
在铁架台的竖杆上缠上白纸条,纸上等距离的画上四、五条红线,这样砝码升高的距离和绳子自由端移动的距离可以直接从中找出倍数关系或读出格数,研究滑轮组时也同样.钩码尽可能大些,滑轮质量尽可能小些.
如下图所示,如果用定滑轮和动滑轮分别拉同一个物体,物体升高一格,绳子的另一端分别升高多少格?如果物体升高两格呢?将有关数据记录到表格中。
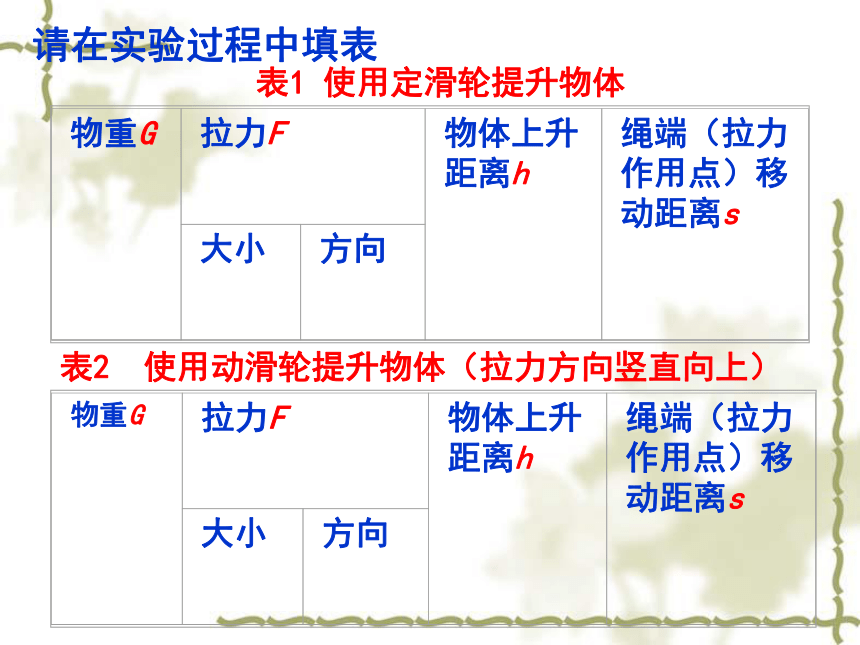
表1 使用定滑轮提升物体
表2 使用动滑轮提升物体(拉力方向竖直向上)
物重G
拉力F
物体上升距离h
绳端(拉力作用点)移动距离s
大小
方向
物重G
拉力F
物体上升距离h
绳端(拉力作用点)移动距离s
大小
方向
请在实验过程中填表
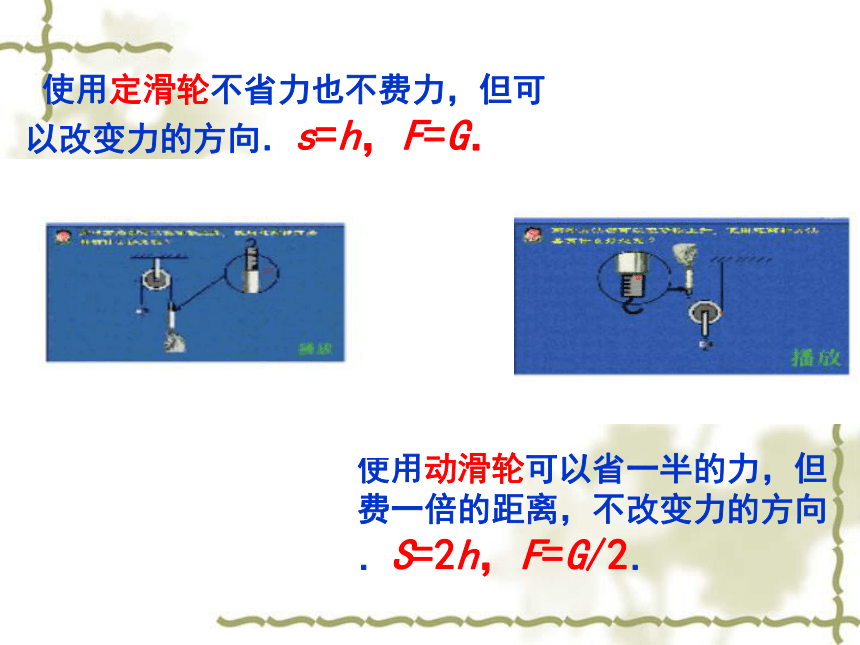
使用定滑轮不省力也不费力,但可以改变力的方向.s=h,F=G.
使用动滑轮可以省一半的力,但费一倍的距离,不改变力的方向.S=2h,F=G/2.
定滑轮的实质
F1
F2
O
L1=L2
F2
F1
O
L1=L2
L1
L2
L1
L2
定滑轮
L1
L2
.0
1:定滑轮实际上就是等臂杠杆。
A:支点在轴心O处。
B:动力臂L1等于阻力臂L2
2:不计摩擦时,拉力大小等于重物的重力大小。( F=G)
3:拉力的方向与重物移动的方向相反。
结论:使用定滑轮不省__,但可以改变施力的___。
力
F
G
方向
F
F
动滑轮的实质
F1
F2
O
O
·
L1
L2
L1 =2L2
F1 = F2 /2
F
G
动滑轮
L2
L1
A:支点在边缘O处
B:动力臂L1为阻力臂L2的2倍。
动力F为阻力G的
倍
1
2
1
2
即F=
G
1:动滑轮实质是动力臂为阻力臂2倍的杠杆。
2:在上述情况下,动力是阻力的
1
2
1
2
F=
G
即
3:拉力的方向与重物的移动方向相同。
结论:使用动滑轮可以___,但不能改变施力的___。
省力
方向
O
.
结论:
1.定滑轮:
(1) 可以改变力的方向
(2) 不省力也不费力
(3) 不省也不费距离
(4) 实质:L1=L2(等臂杠杆) F1=F2
2.动滑轮:
(1) 不改变力的方向
(2) 省一半力
(3) 要多移动距离
(4) 实质:L1=2L2
(动力臂为阻力臂二倍的杠杆 )F1=1/2F2
定滑轮虽然能改变力的方向,使我们工作方便,但不能省力;
于是人们就把定滑轮和动滑轮组合起来使用,把它们各自的优点结合起来,这样就组成了滑轮组.
而动滑轮虽然能省一半力,但不能改变力的方向,使用时经常感觉不便.
为了既省力又能改变力的方向,可以把定滑轮和动滑轮组合起来组成滑轮组。
用以下的动滑轮和定滑轮,可以组成怎样的滑轮组呢?
1:滑轮组
由一个定滑轮和一个动滑轮组成。
F
F
F
G
G
G
实验结果:
1
2
F=
G
1
3
F=
G
1
2
F=
G
拉力F的大小与吊起动滑轮的绳子段数n有关。
n=2
n=2
n=3
A.探究一个定滑轮和一个动滑轮组成滑轮组的绕线方法;
B.探究由一个定滑轮和一个动滑轮组成的滑轮组的省力情况及移动距离的情况.
1.绕成两段绳子承担重物,由铁架台竖杆上的等距离红线格测定动力作用点(绳端)移动的距离 s和砝码升高的距离 h的关系.
结论:可知F=G/2,s =2h.
2.绕成三段绳子承担重物,分别用弹簧测力计拉动力的大小;由弹簧测力计竖直向上拉测动力的大小;两个距离仍由铁架台竖杆上的等距离红线格测定.
结论:可知F=G/3,s=3h.
注意:上图中,甲乙两个物体各由几段绳子承担?
提起物体所用的力与滑轮组用几条绳子吊着物体有什么关系?
C.探究由两个定滑轮和两个动滑轮组成的滑轮组的省力情况及移动距离的情况.
1.绕成四段绳子承担重物.得出结论:F=G/4,s=4h.
2.绕成五段绳子承担重物.得出结论:F=G/5,s=5h.
F=(G+G’)/5
F=(G+G’)/4
结论:若动滑轮重和摩擦力忽略不计,使用滑轮组时,滑轮组由几段绳子吊着物体,提起重物所用的力就等于物重的几分之一。
1
n
F=
G
实验表明,使用滑轮组吊重物时,若动滑轮重和摩擦力忽略不计,动滑轮被几段绳子吊起,所用力就是物重的几分之一即
思考题:
在左图所示的滑轮组中,
(a)若动滑轮重G/不计,拉力F是多少?
(b)若动滑轮重G/不能忽略,那么图中的拉力F应等于多少?
G/
G
F
1
5
F=
G
1
5
F=
(G+G/)
分析:图中吊起动滑轮的绳子段数为5
F
.
2:滑轮组
实验表明,使用滑轮组拉重物时,若动滑轮重和摩擦不计,动滑轮被几段绳子拉住,所用的力就是物体与接触面摩擦力的几分之一。即
1
3
F=
f
f
N
G
T
如图所示,拉力F的大小等于____。
1
n
F=
f
使用滑轮组的时候,重物和动滑轮的总重由几段绳子承担,提起重物所用的动力就是总重的几分之一,动力(或绳子自由端)移动的距离s就是重物升高的距离h的几倍.即F=G/n,s=nh.n为绳子的段数,省了力就要多移动距离,不可能既省力又省距离。
若动滑轮重不可忽略,上述力的关系式应写成F=(G物+G动)/n.
巩固练习
2.如下图(a)所示,物体B重100N,在力F作用下匀速上升时,F应等于___N。(摩擦力忽略不计)
图(a)
F
3. 如上图(b)所示,物体A重为100N,挂重物的钩子承受的拉力是___N。人匀速拉绳子的力是___N(动滑轮自重不计)
图(b)
100
100
50
4.如图所示的四个滑轮组中,图___可省一半力,图___最费力,图___和图____用力大小一样。
(a)
(b)
(c)
(d)
( b )
( c )
(a)
(d)
5.如图所示,物体A重G=80N,在F=60N拉力下匀速前进,此时物体A受到的摩擦力等于__N。(滑轮自重及绳子与滑轮的摩擦不计)
A
F
.
f
T
N
G
1:竖直方向上有一对平衡力N和G
2:水平方向上有一对平衡力T和f
G=N=80N
T=f=120N
1
2
F=
f
因为
所以
f=2F=120N
综合分析得:
120
1.定滑轮:
(1)使用特点:可以改变力的方向,不省力也不费力;不省距离也不费距离.
(2)实质:是一个等臂杠杆.
2.动滑轮:
(1)使用特点:能省一半力,但不改变力的方向;要多移动一倍距离.
(2)实质:动力臂是阻力臂二倍的杠杆.
3.滑轮组:
(1)使用优点:既可省力,又可改变力的方向;但不能既省力又省距离.
(2)公式:F=G总/n=(G物+G动滑轮)/n (不计滑轮摩擦)
s=nh
二、滑轮
1.认识定滑轮和动滑轮。
2.知道定滑轮、动滑轮、滑轮组的作用。
3.会根据要求使用和组装滑轮组。
4.了解其他简单机械的一些应用。
教学目标
复习提问:
1. 杠杆的平衡条件?
2.杠杆的应用:
杠杆一般可以分为 杠杆和 杠杆。如右图所示,图一所应用到的是 杠杆,图二所应用到的是 杠杆。
(图一)
(图二)
F1L1=F2L2
省力
费力
省力
费力
新课引入:
上一节课所学的杠杆是一种简单的机械,在这一节里我们将继续学习另一种简单机械。首先,请同学们看一看上图,你能帮助他们解决这个问题吗?
滑轮在使用时,根据轴的位置是否移动,分为定滑轮和动滑轮两种。
使用时,轴固定不动,叫定滑轮。
使用时,轴和重物一起移动,叫动滑轮。
在日常生活中我们经常可以看到定滑轮和动滑轮,同学们能再举出一些例子吗?请说明它们分别是哪一类滑轮。
(图一)定滑轮的应用
(图二)动滑轮的应用
生活中的滑轮
图A
图B
图C
图D
以下是滑轮常见的几种应用:
实验:研究使用定滑轮或动滑轮提升物体时,分别在用力大小、方向以及移动距离方面的特点.
在铁架台的竖杆上缠上白纸条,纸上等距离的画上四、五条红线,这样砝码升高的距离和绳子自由端移动的距离可以直接从中找出倍数关系或读出格数,研究滑轮组时也同样.钩码尽可能大些,滑轮质量尽可能小些.
如下图所示,如果用定滑轮和动滑轮分别拉同一个物体,物体升高一格,绳子的另一端分别升高多少格?如果物体升高两格呢?将有关数据记录到表格中。
表1 使用定滑轮提升物体
表2 使用动滑轮提升物体(拉力方向竖直向上)
物重G
拉力F
物体上升距离h
绳端(拉力作用点)移动距离s
大小
方向
物重G
拉力F
物体上升距离h
绳端(拉力作用点)移动距离s
大小
方向
请在实验过程中填表
使用定滑轮不省力也不费力,但可以改变力的方向.s=h,F=G.
使用动滑轮可以省一半的力,但费一倍的距离,不改变力的方向.S=2h,F=G/2.
定滑轮的实质
F1
F2
O
L1=L2
F2
F1
O
L1=L2
L1
L2
L1
L2
定滑轮
L1
L2
.0
1:定滑轮实际上就是等臂杠杆。
A:支点在轴心O处。
B:动力臂L1等于阻力臂L2
2:不计摩擦时,拉力大小等于重物的重力大小。( F=G)
3:拉力的方向与重物移动的方向相反。
结论:使用定滑轮不省__,但可以改变施力的___。
力
F
G
方向
F
F
动滑轮的实质
F1
F2
O
O
·
L1
L2
L1 =2L2
F1 = F2 /2
F
G
动滑轮
L2
L1
A:支点在边缘O处
B:动力臂L1为阻力臂L2的2倍。
动力F为阻力G的
倍
1
2
1
2
即F=
G
1:动滑轮实质是动力臂为阻力臂2倍的杠杆。
2:在上述情况下,动力是阻力的
1
2
1
2
F=
G
即
3:拉力的方向与重物的移动方向相同。
结论:使用动滑轮可以___,但不能改变施力的___。
省力
方向
O
.
结论:
1.定滑轮:
(1) 可以改变力的方向
(2) 不省力也不费力
(3) 不省也不费距离
(4) 实质:L1=L2(等臂杠杆) F1=F2
2.动滑轮:
(1) 不改变力的方向
(2) 省一半力
(3) 要多移动距离
(4) 实质:L1=2L2
(动力臂为阻力臂二倍的杠杆 )F1=1/2F2
定滑轮虽然能改变力的方向,使我们工作方便,但不能省力;
于是人们就把定滑轮和动滑轮组合起来使用,把它们各自的优点结合起来,这样就组成了滑轮组.
而动滑轮虽然能省一半力,但不能改变力的方向,使用时经常感觉不便.
为了既省力又能改变力的方向,可以把定滑轮和动滑轮组合起来组成滑轮组。
用以下的动滑轮和定滑轮,可以组成怎样的滑轮组呢?
1:滑轮组
由一个定滑轮和一个动滑轮组成。
F
F
F
G
G
G
实验结果:
1
2
F=
G
1
3
F=
G
1
2
F=
G
拉力F的大小与吊起动滑轮的绳子段数n有关。
n=2
n=2
n=3
A.探究一个定滑轮和一个动滑轮组成滑轮组的绕线方法;
B.探究由一个定滑轮和一个动滑轮组成的滑轮组的省力情况及移动距离的情况.
1.绕成两段绳子承担重物,由铁架台竖杆上的等距离红线格测定动力作用点(绳端)移动的距离 s和砝码升高的距离 h的关系.
结论:可知F=G/2,s =2h.
2.绕成三段绳子承担重物,分别用弹簧测力计拉动力的大小;由弹簧测力计竖直向上拉测动力的大小;两个距离仍由铁架台竖杆上的等距离红线格测定.
结论:可知F=G/3,s=3h.
注意:上图中,甲乙两个物体各由几段绳子承担?
提起物体所用的力与滑轮组用几条绳子吊着物体有什么关系?
C.探究由两个定滑轮和两个动滑轮组成的滑轮组的省力情况及移动距离的情况.
1.绕成四段绳子承担重物.得出结论:F=G/4,s=4h.
2.绕成五段绳子承担重物.得出结论:F=G/5,s=5h.
F=(G+G’)/5
F=(G+G’)/4
结论:若动滑轮重和摩擦力忽略不计,使用滑轮组时,滑轮组由几段绳子吊着物体,提起重物所用的力就等于物重的几分之一。
1
n
F=
G
实验表明,使用滑轮组吊重物时,若动滑轮重和摩擦力忽略不计,动滑轮被几段绳子吊起,所用力就是物重的几分之一即
思考题:
在左图所示的滑轮组中,
(a)若动滑轮重G/不计,拉力F是多少?
(b)若动滑轮重G/不能忽略,那么图中的拉力F应等于多少?
G/
G
F
1
5
F=
G
1
5
F=
(G+G/)
分析:图中吊起动滑轮的绳子段数为5
F
.
2:滑轮组
实验表明,使用滑轮组拉重物时,若动滑轮重和摩擦不计,动滑轮被几段绳子拉住,所用的力就是物体与接触面摩擦力的几分之一。即
1
3
F=
f
f
N
G
T
如图所示,拉力F的大小等于____。
1
n
F=
f
使用滑轮组的时候,重物和动滑轮的总重由几段绳子承担,提起重物所用的动力就是总重的几分之一,动力(或绳子自由端)移动的距离s就是重物升高的距离h的几倍.即F=G/n,s=nh.n为绳子的段数,省了力就要多移动距离,不可能既省力又省距离。
若动滑轮重不可忽略,上述力的关系式应写成F=(G物+G动)/n.
巩固练习
2.如下图(a)所示,物体B重100N,在力F作用下匀速上升时,F应等于___N。(摩擦力忽略不计)
图(a)
F
3. 如上图(b)所示,物体A重为100N,挂重物的钩子承受的拉力是___N。人匀速拉绳子的力是___N(动滑轮自重不计)
图(b)
100
100
50
4.如图所示的四个滑轮组中,图___可省一半力,图___最费力,图___和图____用力大小一样。
(a)
(b)
(c)
(d)
( b )
( c )
(a)
(d)
5.如图所示,物体A重G=80N,在F=60N拉力下匀速前进,此时物体A受到的摩擦力等于__N。(滑轮自重及绳子与滑轮的摩擦不计)
A
F
.
f
T
N
G
1:竖直方向上有一对平衡力N和G
2:水平方向上有一对平衡力T和f
G=N=80N
T=f=120N
1
2
F=
f
因为
所以
f=2F=120N
综合分析得:
120
1.定滑轮:
(1)使用特点:可以改变力的方向,不省力也不费力;不省距离也不费距离.
(2)实质:是一个等臂杠杆.
2.动滑轮:
(1)使用特点:能省一半力,但不改变力的方向;要多移动一倍距离.
(2)实质:动力臂是阻力臂二倍的杠杆.
3.滑轮组:
(1)使用优点:既可省力,又可改变力的方向;但不能既省力又省距离.
(2)公式:F=G总/n=(G物+G动滑轮)/n (不计滑轮摩擦)
s=nh
