【班海】2022-2023春季人教新版 五下 第三单元 2.长方体和正方体的表面积 【优质课件】
文档属性
| 名称 | 【班海】2022-2023春季人教新版 五下 第三单元 2.长方体和正方体的表面积 【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 14:07:25 | ||
图片预览









文档简介
(共38张PPT)
长方体和正方体的表面积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
01 课前导入
03 学以致用
02 新课精讲
04 课堂小结
01
课前导入
情景导入
1.长方形和正方形的面积怎么计算呢?
正方形面积:边长×边长
长方形面积:长×宽
2.长方体和正方体的表面积怎么计算呢?一起看我们的新课吧。
02
新课精讲
探索新知
探究点 1
长方体、正方体的展开图
把一个长方体或正方体的纸盒展开是什么形状的呢
探索新知
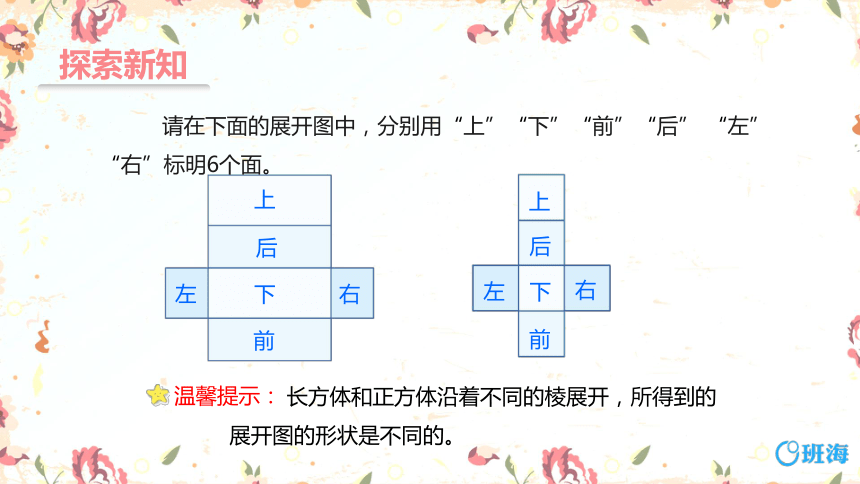
请在下面的展开图中,分别用“上”“下”“前”“后” “左” “右”标明6个面。
下
后
上
前
左
右
下
后
上
前
左
右
温馨提示:
长方体和正方体沿着不同的棱展开,所得到的
展开图的形状是不同的。
探索新知
探究点 2
长方体、正方体表面积意义
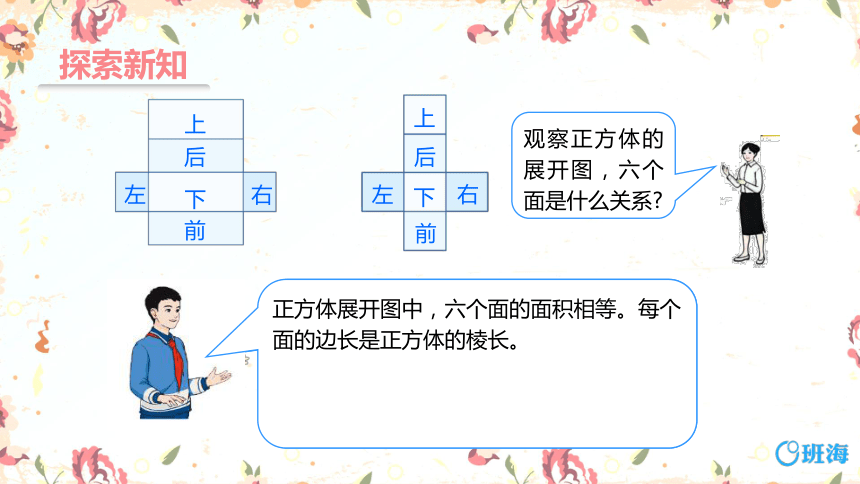
观察长方体展开图,哪些面的面积相等 每个面的长和宽与长方体的长、宽、高有什么关系
下
后
上
前
左
右
探索新知
长方体展开图中,长方体“上面”与“下面”,“前面”与“后面”,“左面”与“右面”的面积分别相等。每个面的长和宽分别是长方体的长、宽、高。
下
后
上
前
左
右
下
后
上
前
左
右
观察正方体的展开图,六个面是什么关系
正方体展开图中,六个面的面积相等。每个面的边长是正方体的棱长。
探索新知
你能利用手中的长方体和正方体,用手摸一摸它们的表面吗?
长方体和正方体的表面积是什么?
长方体或正方体6个面的总面积,叫做它的表面积。
探索新知
探究点 3
长方体的表面积计算方法
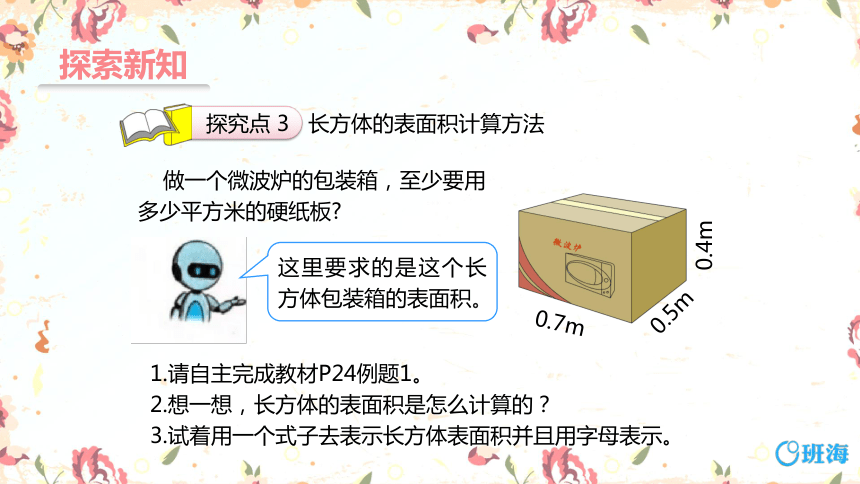
做一个微波炉的包装箱,至少要用多少平方米的硬纸板
0.7m
0.5m
0.4m
这里要求的是这个长方体包装箱的表面积。
1.请自主完成教材P24例题1。
2.想一想,长方体的表面积是怎么计算的?
3.试着用一个式子去表示长方体表面积并且用字母表示。
探索新知
上、下每个面,长_____,宽_____,面积是_______;
前、后每个面,长_____,宽_____,面积是_______;
左、右每个面,长_____,宽_____,面积是_______。
0.7m
0.5m
0.35m2
0.7m
0.4m
0.28m2
0.5m
0.4m
0.2m2
0.7m
0.5m
0.4m
这个包装箱的表面积是:
0.35×2+0.28×2+0.2×2
=0.7+0.56+0.4
=1.66(m2)
答:至少要用1.66m2的硬纸板。
探索新知
长方体表面积=(长×宽+长×高+宽×高)×2
S=2(ab+ah+bh)
长方体表面积=长×宽×2 +长×高×2 +宽×高×2
S=2ab+2ah+2bh
或
探索新知
探究点 4
正方体的表面积计算方法
一个正方体墨水盒,棱长为6.5cm。制作这个墨水盒至少需要多少平方厘米的硬纸板?
求至少用多少平方厘米的硬纸板,就是要求什么 自己试一试!
探索新知
6.5×6.5×6
=42.25×6
=253.5(cm2)
答:制作这个墨水盒至少需要253.5cm2的硬纸板。
探索新知
正方体表面积=棱长×棱长×6
S=6a2
想一想,正方体表面积的计算方法是什么?
探索新知
长方体和正方体的表面积计算方法
1.长方体的表面积:如果用字母a、b、h分别表示长
方体的长、宽和高,用S表示长方体的表面积,则
S=2ab+2ah+2bh或S=2(ab+ah+bh)。
2.正方体的表面积:如果用字母a表示正方体的棱长,
用S表示正方体的表面积,则S=6a2。
典题精讲
( )
( )
( )
√
×
√
折叠后,哪些图形能围成左侧的正方体 在括号中画“√”。
典题精讲
1.亮亮家要给一个长0.75m、宽0.5m、高1.6m的简易衣柜换布罩(如下图,没有底面)。至少需要用布多少平方米
0.75×0.5+0.5×1.6×2+0.75×1.6×2
=0.375+1.6+2.4
=4.375(m2)
答:至少需要用布4.375m2。
典题精讲
2.一个新建的游泳池长50 m,长是宽的2倍,深2.5米。现在是在游泳池的四周和店面贴上瓷砖,一共需要贴多少平方米的瓷砖?
50÷2=25(m)
50×25+50×2.5×2+25×2.5×2=1625(m2)
答:一共需要贴1625 m2的瓷砖。
典题精讲
3.学校要粉刷新教师。已知教师的长是8 m,宽是6米,高是3 m,门窗的面积是11.4 m2。如果每平方米要花4元涂料费,粉刷这个教师需要花费多少钱?
(8×6+8×3×2+6×3×2-11.4)×4=482.4(元)
答:粉刷这个教室需要花费482.4元。
典题精讲
4. 一个玻璃鱼缸的形状是正方体,棱长3dm。制作这个鱼缸时至少需要玻璃多少平方分米 (上面没有盖。)
3×3×5=45(dm2)
答:制作这个鱼缸时至少需要玻璃45dm2。
典题精讲
5.一个正方体礼品盒,棱长1.2dm。如果保证这个礼品盒的用纸是其面积的1.5倍,至少要用多少平方分米的包装纸?
1.2×1.2×6×1.5=12.96(dm2)
答:至少要用12.96 dm2的包装纸。
典题精讲
6.如何把这个长方体木块分成两个棱长为4 cm的正方体?
长方体的长为8 cm,左、右两个面均是边长为4 cm的正方形,应沿长方体的长的中点切开。切完后多了2个面,两个棱长为4 cm的正方体的总表面积与这个长方体的表面积不相等。
03
学以致用
小试牛刀
1.填空。
(1)如图所示,这个展开图能折成一个长方体(字母露在外面),如果F面在前面,从左面看是B面,那么( )面在上面,( )面在后面。
(2)①上、下每个面的长是( ),宽是( ),面积是( )。
②右侧面的长是( ),宽是( ),面积是( )。
C
A
8 cm
5 cm
40 cm2
5 cm
4 cm
20 cm2
小试牛刀
2.选择。
(1)下列图形中,能折成正方体的是( )。
(2)选项中有4个立方体,其中是用右边图形折成的是( )。
ABD
AB
小试牛刀
3.如图所示,这个展开图能折成一个长方体(字母露在外面),如果F面在前面,从左面看是B面,那么( )面在上面,( )面在后面。
C
A
小试牛刀
4.将“展开图”与“立体图形”连起来。
①
②
③
④
⑤
⑥
小试牛刀
5.填空。
(1)上、下每个面,长( ),宽( ),面积是( )。
(2)前、后每个面,长( ),宽( ),面积是( )。
(3)左、右每个面,长( ),宽( ),面积是( )。
(4)这个长方体的表面积是( )。
1.2m
0.8m
0.96m2
1.2m
0.6m
0.72m2
0.8m
0.6m
0.48m2
4.32m2
小试牛刀
6.选择。
(1)挖一个长8 m、宽6 m、深4.5 m的长方体水池,这个水池的占地面积是( )。
A.48 m2 B.44 m2 C.36 m2 D.27 m2
(2)求做一个抽屉用多少木板,是求这个抽屉( )个面的面积。
A.3 B.4 C.5 D.6
(3)下图是一个长方体纸盒的展开图(单位:cm),它的表面积是( )。
A.220 cm2 B.520 cm2 C.700 cm2 D.750 cm2
A
C
A
小试牛刀
7.填空。
(1)这个正方体的棱长和是( )。
(2)每个面的面积是( )。
(3)这个正方体的表面积是( )。
96 cm
64 cm2
384 cm2
小试牛刀
8.计算下列图形的表面积。
(1)
(2)
(9×6+9×5+6×5)×2=258(cm2)
答:图形的表面积为258平方厘米。
12×8×4+8×8×2=512(cm2)
答:图形的表面积为512平方厘米。
(3)
15×15×6=1350(cm2)
答:图形的表面积为1350平方厘米。
小试牛刀
9.一种长方体铁皮通风管长2 m,管口是边长为3 dm的正方形,做30根这样的通风管,至少需要多少平方米的铁皮?
3 dm=0.3 m
2×0.3×4×30=72(m2)
答:至少需要72平方米的铁皮。
小试牛刀
10.一间会议室长20 m,宽8 m,高4 m,要粉刷四周墙壁和天花板,除去门窗的面积40 m2,粉刷的面积是多少平方米?
(20×4+8×4)×2+20×8-40=344(m2)
答:粉刷的面积是344平方米。
04
课堂小结
归纳总结:
长方体和正方体表面积的意义:
长方体或正方体6个面的总面积,叫做它的表面积。
长方体和正方体的表面积计算方法:
1.长方体的表面积计算方法:
S=2(ab+ah+bh)
S=2ab+2ah+2bh
或
2.正方体的表面积计算方法:
S=6a2
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
长方体和正方体的表面积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
01 课前导入
03 学以致用
02 新课精讲
04 课堂小结
01
课前导入
情景导入
1.长方形和正方形的面积怎么计算呢?
正方形面积:边长×边长
长方形面积:长×宽
2.长方体和正方体的表面积怎么计算呢?一起看我们的新课吧。
02
新课精讲
探索新知
探究点 1
长方体、正方体的展开图
把一个长方体或正方体的纸盒展开是什么形状的呢
探索新知
请在下面的展开图中,分别用“上”“下”“前”“后” “左” “右”标明6个面。
下
后
上
前
左
右
下
后
上
前
左
右
温馨提示:
长方体和正方体沿着不同的棱展开,所得到的
展开图的形状是不同的。
探索新知
探究点 2
长方体、正方体表面积意义
观察长方体展开图,哪些面的面积相等 每个面的长和宽与长方体的长、宽、高有什么关系
下
后
上
前
左
右
探索新知
长方体展开图中,长方体“上面”与“下面”,“前面”与“后面”,“左面”与“右面”的面积分别相等。每个面的长和宽分别是长方体的长、宽、高。
下
后
上
前
左
右
下
后
上
前
左
右
观察正方体的展开图,六个面是什么关系
正方体展开图中,六个面的面积相等。每个面的边长是正方体的棱长。
探索新知
你能利用手中的长方体和正方体,用手摸一摸它们的表面吗?
长方体和正方体的表面积是什么?
长方体或正方体6个面的总面积,叫做它的表面积。
探索新知
探究点 3
长方体的表面积计算方法
做一个微波炉的包装箱,至少要用多少平方米的硬纸板
0.7m
0.5m
0.4m
这里要求的是这个长方体包装箱的表面积。
1.请自主完成教材P24例题1。
2.想一想,长方体的表面积是怎么计算的?
3.试着用一个式子去表示长方体表面积并且用字母表示。
探索新知
上、下每个面,长_____,宽_____,面积是_______;
前、后每个面,长_____,宽_____,面积是_______;
左、右每个面,长_____,宽_____,面积是_______。
0.7m
0.5m
0.35m2
0.7m
0.4m
0.28m2
0.5m
0.4m
0.2m2
0.7m
0.5m
0.4m
这个包装箱的表面积是:
0.35×2+0.28×2+0.2×2
=0.7+0.56+0.4
=1.66(m2)
答:至少要用1.66m2的硬纸板。
探索新知
长方体表面积=(长×宽+长×高+宽×高)×2
S=2(ab+ah+bh)
长方体表面积=长×宽×2 +长×高×2 +宽×高×2
S=2ab+2ah+2bh
或
探索新知
探究点 4
正方体的表面积计算方法
一个正方体墨水盒,棱长为6.5cm。制作这个墨水盒至少需要多少平方厘米的硬纸板?
求至少用多少平方厘米的硬纸板,就是要求什么 自己试一试!
探索新知
6.5×6.5×6
=42.25×6
=253.5(cm2)
答:制作这个墨水盒至少需要253.5cm2的硬纸板。
探索新知
正方体表面积=棱长×棱长×6
S=6a2
想一想,正方体表面积的计算方法是什么?
探索新知
长方体和正方体的表面积计算方法
1.长方体的表面积:如果用字母a、b、h分别表示长
方体的长、宽和高,用S表示长方体的表面积,则
S=2ab+2ah+2bh或S=2(ab+ah+bh)。
2.正方体的表面积:如果用字母a表示正方体的棱长,
用S表示正方体的表面积,则S=6a2。
典题精讲
( )
( )
( )
√
×
√
折叠后,哪些图形能围成左侧的正方体 在括号中画“√”。
典题精讲
1.亮亮家要给一个长0.75m、宽0.5m、高1.6m的简易衣柜换布罩(如下图,没有底面)。至少需要用布多少平方米
0.75×0.5+0.5×1.6×2+0.75×1.6×2
=0.375+1.6+2.4
=4.375(m2)
答:至少需要用布4.375m2。
典题精讲
2.一个新建的游泳池长50 m,长是宽的2倍,深2.5米。现在是在游泳池的四周和店面贴上瓷砖,一共需要贴多少平方米的瓷砖?
50÷2=25(m)
50×25+50×2.5×2+25×2.5×2=1625(m2)
答:一共需要贴1625 m2的瓷砖。
典题精讲
3.学校要粉刷新教师。已知教师的长是8 m,宽是6米,高是3 m,门窗的面积是11.4 m2。如果每平方米要花4元涂料费,粉刷这个教师需要花费多少钱?
(8×6+8×3×2+6×3×2-11.4)×4=482.4(元)
答:粉刷这个教室需要花费482.4元。
典题精讲
4. 一个玻璃鱼缸的形状是正方体,棱长3dm。制作这个鱼缸时至少需要玻璃多少平方分米 (上面没有盖。)
3×3×5=45(dm2)
答:制作这个鱼缸时至少需要玻璃45dm2。
典题精讲
5.一个正方体礼品盒,棱长1.2dm。如果保证这个礼品盒的用纸是其面积的1.5倍,至少要用多少平方分米的包装纸?
1.2×1.2×6×1.5=12.96(dm2)
答:至少要用12.96 dm2的包装纸。
典题精讲
6.如何把这个长方体木块分成两个棱长为4 cm的正方体?
长方体的长为8 cm,左、右两个面均是边长为4 cm的正方形,应沿长方体的长的中点切开。切完后多了2个面,两个棱长为4 cm的正方体的总表面积与这个长方体的表面积不相等。
03
学以致用
小试牛刀
1.填空。
(1)如图所示,这个展开图能折成一个长方体(字母露在外面),如果F面在前面,从左面看是B面,那么( )面在上面,( )面在后面。
(2)①上、下每个面的长是( ),宽是( ),面积是( )。
②右侧面的长是( ),宽是( ),面积是( )。
C
A
8 cm
5 cm
40 cm2
5 cm
4 cm
20 cm2
小试牛刀
2.选择。
(1)下列图形中,能折成正方体的是( )。
(2)选项中有4个立方体,其中是用右边图形折成的是( )。
ABD
AB
小试牛刀
3.如图所示,这个展开图能折成一个长方体(字母露在外面),如果F面在前面,从左面看是B面,那么( )面在上面,( )面在后面。
C
A
小试牛刀
4.将“展开图”与“立体图形”连起来。
①
②
③
④
⑤
⑥
小试牛刀
5.填空。
(1)上、下每个面,长( ),宽( ),面积是( )。
(2)前、后每个面,长( ),宽( ),面积是( )。
(3)左、右每个面,长( ),宽( ),面积是( )。
(4)这个长方体的表面积是( )。
1.2m
0.8m
0.96m2
1.2m
0.6m
0.72m2
0.8m
0.6m
0.48m2
4.32m2
小试牛刀
6.选择。
(1)挖一个长8 m、宽6 m、深4.5 m的长方体水池,这个水池的占地面积是( )。
A.48 m2 B.44 m2 C.36 m2 D.27 m2
(2)求做一个抽屉用多少木板,是求这个抽屉( )个面的面积。
A.3 B.4 C.5 D.6
(3)下图是一个长方体纸盒的展开图(单位:cm),它的表面积是( )。
A.220 cm2 B.520 cm2 C.700 cm2 D.750 cm2
A
C
A
小试牛刀
7.填空。
(1)这个正方体的棱长和是( )。
(2)每个面的面积是( )。
(3)这个正方体的表面积是( )。
96 cm
64 cm2
384 cm2
小试牛刀
8.计算下列图形的表面积。
(1)
(2)
(9×6+9×5+6×5)×2=258(cm2)
答:图形的表面积为258平方厘米。
12×8×4+8×8×2=512(cm2)
答:图形的表面积为512平方厘米。
(3)
15×15×6=1350(cm2)
答:图形的表面积为1350平方厘米。
小试牛刀
9.一种长方体铁皮通风管长2 m,管口是边长为3 dm的正方形,做30根这样的通风管,至少需要多少平方米的铁皮?
3 dm=0.3 m
2×0.3×4×30=72(m2)
答:至少需要72平方米的铁皮。
小试牛刀
10.一间会议室长20 m,宽8 m,高4 m,要粉刷四周墙壁和天花板,除去门窗的面积40 m2,粉刷的面积是多少平方米?
(20×4+8×4)×2+20×8-40=344(m2)
答:粉刷的面积是344平方米。
04
课堂小结
归纳总结:
长方体和正方体表面积的意义:
长方体或正方体6个面的总面积,叫做它的表面积。
长方体和正方体的表面积计算方法:
1.长方体的表面积计算方法:
S=2(ab+ah+bh)
S=2ab+2ah+2bh
或
2.正方体的表面积计算方法:
S=6a2
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
