【班海】2022-2023春季人教新版 六下 第三单元 2.2圆锥的体积【优质课件】
文档属性
| 名称 | 【班海】2022-2023春季人教新版 六下 第三单元 2.2圆锥的体积【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 14:18:58 | ||
图片预览






文档简介
(共26张PPT)
圆锥的体积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
01
课前导入
02
新课精讲
03
学以致用
04
课堂小结
01
课前导入
情景导入
我们已经学会计算圆柱的体积,请你回忆一下如何计算圆柱的体积?
02
新课精讲
探索新知
探究点 1
圆锥的体积计算公式的推导
圆柱的底面是圆,圆锥的底面也是圆……
圆锥的体积和圆柱的体积有没有关系呢?
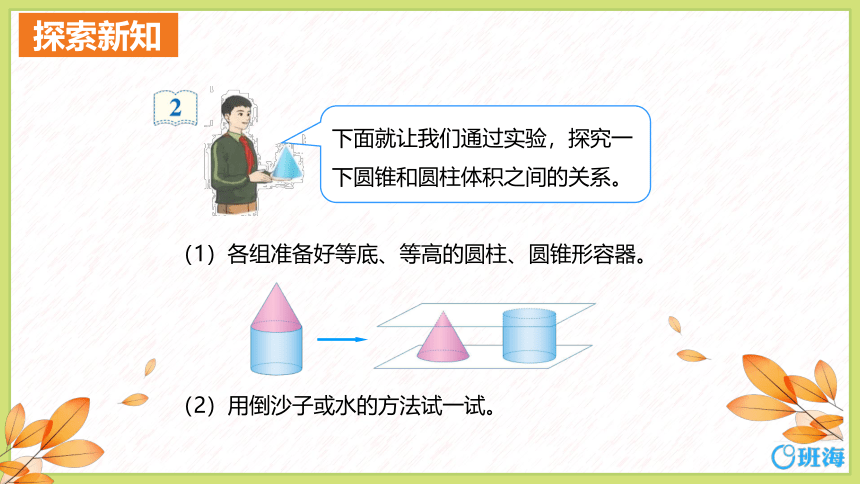
(1)各组准备好等底、等高的圆柱、圆锥形容器。
(2)用倒沙子或水的方法试一试。
下面就让我们通过实验,探究一下圆锥和圆柱体积之间的关系。
探索新知
(3)通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
V
圆锥
=
V
圆柱
=
3
1
3
1
Sh
我把圆柱装满水,再往圆锥里倒。
圆锥装满后,我把沙子倒进盒子里,正好倒了三次。
三次正好倒满。
探索新知
探究点 2
运用圆锥的体积公式解决问题
4m
1.5m
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米
沙子重1.5t,这堆沙子大约重多少吨?
自主学习
1. 首先读题,找出已知和未知。
2. 根据已知和未知确定解题步骤并确定每一步要用到的公式。
3. 写出具体的计算过程,每一步写出所用到的公式。
探索新知
(1)沙堆底面积:S=πr2
3.14 ×( )=3.14×4=12.56(m2)
2
4
2
(2)沙堆的体积:V= sh
3
1
×12.56×1.5=6.28(m )
3
1
(3)沙堆重:
6.28×1.5=9.42(t)
答:这堆沙子大约重9.42吨。
4m
1.5m
探索新知
圆锥的体积
圆锥体积做试验,它与圆柱有关联。
等底等高是条件,三分之一记心间。
统一单位放在前,计算起来想简便。
探索新知
典题精讲
1.一个圆柱和一个圆锥的底面积和体积分别相等。已知圆柱的高是4 dm,圆锥的高是多少?
答:圆锥的高是12 dm。
2.一个圆柱和一个圆锥的体积和高分别相等。已知圆锥的底面积是28.26cm2,圆柱的底面积是多少?
答:圆柱的底面积是9.42 cm2
典题精讲
3. 一个圆锥形的零件,底面积是19cm2,高是12cm,这个零件的体积是多少?
答:这个零件的体积是76cm 。
×19 ×12=76(cm )
3
1
4. 一个用钢铸造成的圆锥形铅锤,底面直径是4cm,高5cm。每立方厘米钢大约重7.8g。这个铅锤重多少克?(得数保留整数)
(2)铅锤的体积:
(1)铅锤底面积:
21×7.8≈163(g)
(3)铅锤的质量:
答:这个铅锤大约重163克 。
×12.56×5≈21(cm3)
3.14×( )=3.14×4=12.56(cm2)
2
4
2
3
1
典题精讲
5.一定时间内,降落在水平地面上的雨水,在未经蒸发、渗漏、流失情况下所积的深度,称为降水量(通常以毫米为单位)。测定降水量常用的一起包括雨量器和量筒。我国气象上规定,按24小时的降水量为标准,降水级别如下页表。
典题精讲
级别 小雨 中雨 大雨 暴雨 大暴雨 特大暴雨
降水量/mm 10以下 10~24.9 25~49.9 50~99.9 100~199.9 200以上
某区的土地面积为1000km2,2012年7月23日平均降水量为220 mm,该日该区总降水为多少亿立方米?该区一年绿化用水为0.4亿立方米,这些积水的20%能满足绿化用水吗?
220 mm=0.22 m
1000 km2=1000000000 m2
1000000000×0.22=220000000(m3)=2.2(亿立方米)
2.2×20%=0.44(亿立方米) 0.44亿立方米>0.4亿立方米
这些雨水的20%能满足绿化用水。
典题精讲
03
学以致用
小试牛刀
1.填空。
(1)圆锥的体积等于和它( )的圆柱体积的( ),所以圆锥的体积=( ),用字母表示是( )。
(2)一个圆柱和一个圆锥等底等高。若圆柱的体积是12.6 dm3,则圆锥的体积是( )dm3;若圆锥的体积是12.6 dm3,则圆柱的体积是( )dm3。
(3)等底等高的圆柱和圆锥的体积的比是( ),圆锥的体积比圆柱的体积少( )。
等底等高
4.2
37.8
3∶1
×底面积×高
V= Sh
2.计算下面各圆锥的体积。
9×3.6×
=32.4×
=10.8(m3)
答:圆锥的体积为10.8立方米。
3.14×42×12×
=3.14×16×12×
=602.88×
=200.96(cm3)
答:圆锥的体积为200.96立方厘米。
小试牛刀
3.解决问题。
(1)一个实心铜制圆锥,底面直径是6 cm,高是3 cm。如果每立方厘米铜重8.9 g,这个实心铜制圆锥约重多少克?(得数保留整数)
3.14× × 3× ×8.9
=251.514(g)
≈252(g)
答:这个实心铜制圆锥约重252克。
小试牛刀
(2)一个圆锥形帐篷,它的底面半径是3 m,高是2.6 m。帐篷内的空间有多大?
×3.14×32×2.6=24.492(m3)
答:帐篷内的空间有24.492立方米。
小试牛刀
(3)一个圆锥形小麦堆,底面周长是12.56 m,高是1.8 m。如果每立方米小麦约重780 kg,按出粉率80%计算,这堆小麦可磨出多少千克面粉?
12.56÷3.14÷2=2(m)
3.14×22×1.8× ×780×80%=4702.464(kg)
答:这堆小麦可磨出4702.464千克面粉。
小试牛刀
4.判断。(对的画“√”,错的画“×”)
(1)圆柱的体积是圆锥体积的3倍。 ( )
(2)如果一个圆锥的体积是一个圆柱体积的 ,那么这个圆锥和这个圆柱一定等底等高。 ( )
(3)一个圆锥体和一个圆柱体的底面积相等,圆柱体的高是圆锥体高的3倍,这个圆锥体的体积与圆柱体体积的比是1∶9。 ( )
(4)一个圆锥体的体积比与它等底等高的圆柱体体积小 。 ( )
(5) 圆锥的高是圆柱高的3倍,它们体积一定相等。 ( )
×
×
√
√
×
小试牛刀
04
课堂小结
归纳总结:
圆锥的体积等于与它等底等高的圆柱体积的 。
2. 圆锥的体积公式用字母表示为V= Sh或V= πr h。
3. 当已知圆锥的底面直径和高,可利用公式
V= π( ) h来计算圆锥的体积。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
圆锥的体积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
01
课前导入
02
新课精讲
03
学以致用
04
课堂小结
01
课前导入
情景导入
我们已经学会计算圆柱的体积,请你回忆一下如何计算圆柱的体积?
02
新课精讲
探索新知
探究点 1
圆锥的体积计算公式的推导
圆柱的底面是圆,圆锥的底面也是圆……
圆锥的体积和圆柱的体积有没有关系呢?
(1)各组准备好等底、等高的圆柱、圆锥形容器。
(2)用倒沙子或水的方法试一试。
下面就让我们通过实验,探究一下圆锥和圆柱体积之间的关系。
探索新知
(3)通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
V
圆锥
=
V
圆柱
=
3
1
3
1
Sh
我把圆柱装满水,再往圆锥里倒。
圆锥装满后,我把沙子倒进盒子里,正好倒了三次。
三次正好倒满。
探索新知
探究点 2
运用圆锥的体积公式解决问题
4m
1.5m
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米
沙子重1.5t,这堆沙子大约重多少吨?
自主学习
1. 首先读题,找出已知和未知。
2. 根据已知和未知确定解题步骤并确定每一步要用到的公式。
3. 写出具体的计算过程,每一步写出所用到的公式。
探索新知
(1)沙堆底面积:S=πr2
3.14 ×( )=3.14×4=12.56(m2)
2
4
2
(2)沙堆的体积:V= sh
3
1
×12.56×1.5=6.28(m )
3
1
(3)沙堆重:
6.28×1.5=9.42(t)
答:这堆沙子大约重9.42吨。
4m
1.5m
探索新知
圆锥的体积
圆锥体积做试验,它与圆柱有关联。
等底等高是条件,三分之一记心间。
统一单位放在前,计算起来想简便。
探索新知
典题精讲
1.一个圆柱和一个圆锥的底面积和体积分别相等。已知圆柱的高是4 dm,圆锥的高是多少?
答:圆锥的高是12 dm。
2.一个圆柱和一个圆锥的体积和高分别相等。已知圆锥的底面积是28.26cm2,圆柱的底面积是多少?
答:圆柱的底面积是9.42 cm2
典题精讲
3. 一个圆锥形的零件,底面积是19cm2,高是12cm,这个零件的体积是多少?
答:这个零件的体积是76cm 。
×19 ×12=76(cm )
3
1
4. 一个用钢铸造成的圆锥形铅锤,底面直径是4cm,高5cm。每立方厘米钢大约重7.8g。这个铅锤重多少克?(得数保留整数)
(2)铅锤的体积:
(1)铅锤底面积:
21×7.8≈163(g)
(3)铅锤的质量:
答:这个铅锤大约重163克 。
×12.56×5≈21(cm3)
3.14×( )=3.14×4=12.56(cm2)
2
4
2
3
1
典题精讲
5.一定时间内,降落在水平地面上的雨水,在未经蒸发、渗漏、流失情况下所积的深度,称为降水量(通常以毫米为单位)。测定降水量常用的一起包括雨量器和量筒。我国气象上规定,按24小时的降水量为标准,降水级别如下页表。
典题精讲
级别 小雨 中雨 大雨 暴雨 大暴雨 特大暴雨
降水量/mm 10以下 10~24.9 25~49.9 50~99.9 100~199.9 200以上
某区的土地面积为1000km2,2012年7月23日平均降水量为220 mm,该日该区总降水为多少亿立方米?该区一年绿化用水为0.4亿立方米,这些积水的20%能满足绿化用水吗?
220 mm=0.22 m
1000 km2=1000000000 m2
1000000000×0.22=220000000(m3)=2.2(亿立方米)
2.2×20%=0.44(亿立方米) 0.44亿立方米>0.4亿立方米
这些雨水的20%能满足绿化用水。
典题精讲
03
学以致用
小试牛刀
1.填空。
(1)圆锥的体积等于和它( )的圆柱体积的( ),所以圆锥的体积=( ),用字母表示是( )。
(2)一个圆柱和一个圆锥等底等高。若圆柱的体积是12.6 dm3,则圆锥的体积是( )dm3;若圆锥的体积是12.6 dm3,则圆柱的体积是( )dm3。
(3)等底等高的圆柱和圆锥的体积的比是( ),圆锥的体积比圆柱的体积少( )。
等底等高
4.2
37.8
3∶1
×底面积×高
V= Sh
2.计算下面各圆锥的体积。
9×3.6×
=32.4×
=10.8(m3)
答:圆锥的体积为10.8立方米。
3.14×42×12×
=3.14×16×12×
=602.88×
=200.96(cm3)
答:圆锥的体积为200.96立方厘米。
小试牛刀
3.解决问题。
(1)一个实心铜制圆锥,底面直径是6 cm,高是3 cm。如果每立方厘米铜重8.9 g,这个实心铜制圆锥约重多少克?(得数保留整数)
3.14× × 3× ×8.9
=251.514(g)
≈252(g)
答:这个实心铜制圆锥约重252克。
小试牛刀
(2)一个圆锥形帐篷,它的底面半径是3 m,高是2.6 m。帐篷内的空间有多大?
×3.14×32×2.6=24.492(m3)
答:帐篷内的空间有24.492立方米。
小试牛刀
(3)一个圆锥形小麦堆,底面周长是12.56 m,高是1.8 m。如果每立方米小麦约重780 kg,按出粉率80%计算,这堆小麦可磨出多少千克面粉?
12.56÷3.14÷2=2(m)
3.14×22×1.8× ×780×80%=4702.464(kg)
答:这堆小麦可磨出4702.464千克面粉。
小试牛刀
4.判断。(对的画“√”,错的画“×”)
(1)圆柱的体积是圆锥体积的3倍。 ( )
(2)如果一个圆锥的体积是一个圆柱体积的 ,那么这个圆锥和这个圆柱一定等底等高。 ( )
(3)一个圆锥体和一个圆柱体的底面积相等,圆柱体的高是圆锥体高的3倍,这个圆锥体的体积与圆柱体体积的比是1∶9。 ( )
(4)一个圆锥体的体积比与它等底等高的圆柱体体积小 。 ( )
(5) 圆锥的高是圆柱高的3倍,它们体积一定相等。 ( )
×
×
√
√
×
小试牛刀
04
课堂小结
归纳总结:
圆锥的体积等于与它等底等高的圆柱体积的 。
2. 圆锥的体积公式用字母表示为V= Sh或V= πr h。
3. 当已知圆锥的底面直径和高,可利用公式
V= π( ) h来计算圆锥的体积。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
