【班海】2022-2023春季人教新版 六下 第四单元 2.2反比例【优质课件】
文档属性
| 名称 | 【班海】2022-2023春季人教新版 六下 第四单元 2.2反比例【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
反比例
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
01
学以致用
03
新课精讲
02
课堂小结
04
课前导入
情景导入
有正比例是不是就有反比例呢?有什么不同呢?
成正比例的量有什么特征?
(3)两种量中相对应的两个数的比值一定。
(1)两种相关联的量。
(2)一种量变化,另一种量也随着变化。
新课精讲
探索新知
探究点
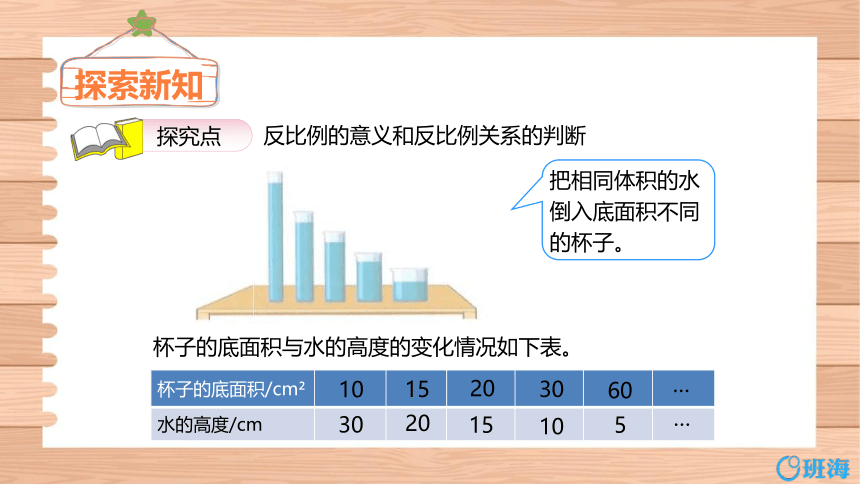
反比例的意义和反比例关系的判断
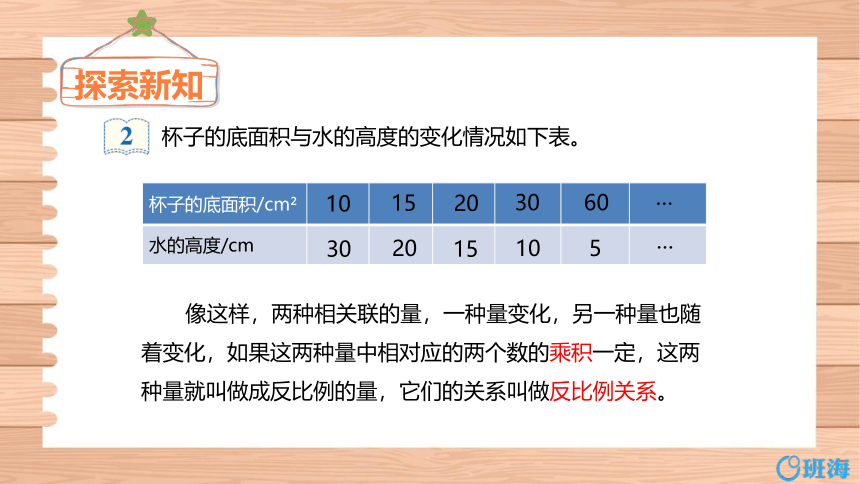
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
把相同体积的水倒入底面积不同的杯子。
探索新知
观察上表,回答下面的问题。
(1)表中有哪两种量?
(2)水的高度是怎样随着杯子底面积的大小变化而变化的?
(3)相对应的杯子的底面积与水的高度的乘积分别是多少?
你能发现什么?
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
探索新知
从上表可以看出,水的高度和杯子的底面积是两种相关联的量,水的高度是随着杯子的底面积的变大而不断变小的,而且水的高度与杯子的底面积的乘积总是一定的。例如:
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
积300,实际就是倒入杯子的水的体积。用式子表示它们的关系就是:
底面积×高度=体积
探索新知
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
探索新知
在上面的实验中,高度和底面积是成反比例的量,高度与底面积成反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用下面的式子表示:
x y=k
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
探索新知
如果长方形的面积一定,长与宽成反比例关系。
如果总价一定,单价与数量成反比例关系。
你能举出生活中反比例关系的例子吗?
探索新知
讨论交流:
以小组为单位,讨论交流下面的问题:
如何判断两个量是否成反比例关系?请举例说明。
提示:
判断两个量是否成反比例关系的基本步骤:
1. 首先判断两个量是否是相关联的量。
2. 然后再看两个量的积是否为定值。
典型例题
每天运的吨数/吨
运货的天数/天
300
1
150
2
100
3
75
4
60
5
50
6
(1)表中有哪两种量?它们是不是相关联的量?
表中有每天运的吨数和运货的天数两种量,它们是相关联的量。
典型例题
每天运的吨数/吨
运货的天数/天
300
1
150
2
100
3
75
4
60
5
50
6
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说一说这个积表示什么。
(3)运货的天数与每天运的吨数成反比例关系吗?为什么?
300×1=300 150×2=300 100×3=300
75×4=300 60×5=300 50×6=300
积相等(一定)。这个积表示这批货的总量。
成反比例关系。因为每天运的吨数和运货的天数是两种相关联的量,而且它们的乘积一定,所以这两种量成反比例关系。
典型例题
1.京沪高铁的火车平均行驶速度与驶完全程所需时间如下表。
速度/(千米/时) 270 260 250 200 180 150 …
时间/时 5 5.2 6.5 …
(1)京沪高铁全长多少千米?
260×5=1300(千米)
典型例题
(2)如果用v表示火车的平均速度,t表示驶完全程所需时间。t与v成什么比例关系?你能写出这个关系式吗?
(3)如果火车的平均速度为325千米/时,驶完全程需要多长时间?
t与v成反比例关系。
tv=1300。
解:设驶完全程需要x时。
x×325=1300
x=4
典型例题
2.有x、y、z三个相关联的量,并有xy=z。
(1)当z一定是,x与y成 比例关系。
(2)当x一定是, z与y成 比例关系。
(3)当y一定是, z与x成 比例关系。
反
正
正
易错提醒
所铺正方形地面的面积一定时,每块方砖的边长和需要的块数成比例关系吗?为什么?
不成比例关系。因为边长×边长×块数=所铺正方形地面的面积。
辨析:判断比例关系时,没有找准相应的量。
学以致用
小试牛刀
1.填空。
(1)某电视机厂装配一批电视机,每天装配的台数和需要的时间如下表:
①表中( )和( )是相关联的量,每天装配的台数( ),则需要的天数( )。
每天装配的
台数/台 60 90 120 180 360 720 …
需要的天数/天 60 40 30 20 10 5 …
每天装配的台数
需要的天数
增多
减少
小试牛刀
②每天装配的台数和对应的需要的天数的乘积都是( ),这个乘积表示( )。
③因为每天装配的台数和对应的需要的天数的乘积一定,所以表中两种量成( )关系。
(2) 如果xy=7.5,那么x和y成( )比例关系。
3600
装配的这批电视机的总台数
反比例
反
小试牛刀
3.判断下面各题中的两种量是否成反比例关系,并说明理由。
(1) 订阅《现代少年报》的总价一定,订阅的份数和报纸的单价。
(2) 用同一批纸装订成同样的作业本,每本的张数和装订的本数。
(3) 发芽率一定,发芽种子数与试验种子数。
成反比例关系,因为份数×单价=总价(一定)。
成反比例关系,因为每本的张数×装订的本数=这批纸的总张数(一定)。
不成反比例关系,因为发芽种子数÷试验种子数=发芽率(一定)。
小试牛刀
4.某运输队运送一批物资,要一次全部运完,每辆车的载重量与所用辆数如下表。
(1) 表中的两种量是相关联的量吗?
(2) 写出表中给出的两种量中相对应的两个数的积,这些积一定吗?
每辆车的载重量/t 2.5 4 5 2
所用辆数/辆 48 30 24 60
表中的两种量是相关联的量。
2.5×48=120 4×30=120 5×24=120 2×60=120
乘积都是120,积一定。
小试牛刀
(3)这个积表示的意义是什么?
(4)表中的两种量成反比例关系吗?为什么?
这个积表示的意义是这批物资的总质量。
表中的两种量成反比例关系。
因为每辆车的载重量×所用辆数=这批物资总质量(一定),所以每辆车的载重量和所用辆数成反比例关系。
小试牛刀
5.填表。
已知y和x成正比例关系,在下表的空格中填写合适的数。
下表中x和y两个量成反比例关系,请把表格填写完整。
x 2 3 12
y 6.4 16 2
x 4 12
y 9 18 3.6 72
9.6
5
0.8
0.625
38.4
2
3
10
54
小试牛刀
6.判断下面两种量成什么比例关系,并说明理由。
(1)时间一定,织布的总米数和每小时织布的米数。
(2)分子一定,分母和分数值。
(3)打同一份稿件,打字的速度和打字所用的时间。
成正比例关系,因为织布的总米数÷每小时织布的米数=时间(一定)。
成反比例关系,因为分母×分数值=分子(一定)。
成反比例关系,因为打字的速度×打字所用的时间=稿件的总字数(一定)。
课堂小结
归纳总结:
反比例的意义:
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
判断两个量是否成反比例关系的基本步骤:
1. 首先判断两个量是否是相关联的量。
2. 然后再看两个量的积是否为定值。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
反比例
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
01
学以致用
03
新课精讲
02
课堂小结
04
课前导入
情景导入
有正比例是不是就有反比例呢?有什么不同呢?
成正比例的量有什么特征?
(3)两种量中相对应的两个数的比值一定。
(1)两种相关联的量。
(2)一种量变化,另一种量也随着变化。
新课精讲
探索新知
探究点
反比例的意义和反比例关系的判断
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
把相同体积的水倒入底面积不同的杯子。
探索新知
观察上表,回答下面的问题。
(1)表中有哪两种量?
(2)水的高度是怎样随着杯子底面积的大小变化而变化的?
(3)相对应的杯子的底面积与水的高度的乘积分别是多少?
你能发现什么?
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
探索新知
从上表可以看出,水的高度和杯子的底面积是两种相关联的量,水的高度是随着杯子的底面积的变大而不断变小的,而且水的高度与杯子的底面积的乘积总是一定的。例如:
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
积300,实际就是倒入杯子的水的体积。用式子表示它们的关系就是:
底面积×高度=体积
探索新知
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
探索新知
在上面的实验中,高度和底面积是成反比例的量,高度与底面积成反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用下面的式子表示:
x y=k
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
探索新知
如果长方形的面积一定,长与宽成反比例关系。
如果总价一定,单价与数量成反比例关系。
你能举出生活中反比例关系的例子吗?
探索新知
讨论交流:
以小组为单位,讨论交流下面的问题:
如何判断两个量是否成反比例关系?请举例说明。
提示:
判断两个量是否成反比例关系的基本步骤:
1. 首先判断两个量是否是相关联的量。
2. 然后再看两个量的积是否为定值。
典型例题
每天运的吨数/吨
运货的天数/天
300
1
150
2
100
3
75
4
60
5
50
6
(1)表中有哪两种量?它们是不是相关联的量?
表中有每天运的吨数和运货的天数两种量,它们是相关联的量。
典型例题
每天运的吨数/吨
运货的天数/天
300
1
150
2
100
3
75
4
60
5
50
6
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说一说这个积表示什么。
(3)运货的天数与每天运的吨数成反比例关系吗?为什么?
300×1=300 150×2=300 100×3=300
75×4=300 60×5=300 50×6=300
积相等(一定)。这个积表示这批货的总量。
成反比例关系。因为每天运的吨数和运货的天数是两种相关联的量,而且它们的乘积一定,所以这两种量成反比例关系。
典型例题
1.京沪高铁的火车平均行驶速度与驶完全程所需时间如下表。
速度/(千米/时) 270 260 250 200 180 150 …
时间/时 5 5.2 6.5 …
(1)京沪高铁全长多少千米?
260×5=1300(千米)
典型例题
(2)如果用v表示火车的平均速度,t表示驶完全程所需时间。t与v成什么比例关系?你能写出这个关系式吗?
(3)如果火车的平均速度为325千米/时,驶完全程需要多长时间?
t与v成反比例关系。
tv=1300。
解:设驶完全程需要x时。
x×325=1300
x=4
典型例题
2.有x、y、z三个相关联的量,并有xy=z。
(1)当z一定是,x与y成 比例关系。
(2)当x一定是, z与y成 比例关系。
(3)当y一定是, z与x成 比例关系。
反
正
正
易错提醒
所铺正方形地面的面积一定时,每块方砖的边长和需要的块数成比例关系吗?为什么?
不成比例关系。因为边长×边长×块数=所铺正方形地面的面积。
辨析:判断比例关系时,没有找准相应的量。
学以致用
小试牛刀
1.填空。
(1)某电视机厂装配一批电视机,每天装配的台数和需要的时间如下表:
①表中( )和( )是相关联的量,每天装配的台数( ),则需要的天数( )。
每天装配的
台数/台 60 90 120 180 360 720 …
需要的天数/天 60 40 30 20 10 5 …
每天装配的台数
需要的天数
增多
减少
小试牛刀
②每天装配的台数和对应的需要的天数的乘积都是( ),这个乘积表示( )。
③因为每天装配的台数和对应的需要的天数的乘积一定,所以表中两种量成( )关系。
(2) 如果xy=7.5,那么x和y成( )比例关系。
3600
装配的这批电视机的总台数
反比例
反
小试牛刀
3.判断下面各题中的两种量是否成反比例关系,并说明理由。
(1) 订阅《现代少年报》的总价一定,订阅的份数和报纸的单价。
(2) 用同一批纸装订成同样的作业本,每本的张数和装订的本数。
(3) 发芽率一定,发芽种子数与试验种子数。
成反比例关系,因为份数×单价=总价(一定)。
成反比例关系,因为每本的张数×装订的本数=这批纸的总张数(一定)。
不成反比例关系,因为发芽种子数÷试验种子数=发芽率(一定)。
小试牛刀
4.某运输队运送一批物资,要一次全部运完,每辆车的载重量与所用辆数如下表。
(1) 表中的两种量是相关联的量吗?
(2) 写出表中给出的两种量中相对应的两个数的积,这些积一定吗?
每辆车的载重量/t 2.5 4 5 2
所用辆数/辆 48 30 24 60
表中的两种量是相关联的量。
2.5×48=120 4×30=120 5×24=120 2×60=120
乘积都是120,积一定。
小试牛刀
(3)这个积表示的意义是什么?
(4)表中的两种量成反比例关系吗?为什么?
这个积表示的意义是这批物资的总质量。
表中的两种量成反比例关系。
因为每辆车的载重量×所用辆数=这批物资总质量(一定),所以每辆车的载重量和所用辆数成反比例关系。
小试牛刀
5.填表。
已知y和x成正比例关系,在下表的空格中填写合适的数。
下表中x和y两个量成反比例关系,请把表格填写完整。
x 2 3 12
y 6.4 16 2
x 4 12
y 9 18 3.6 72
9.6
5
0.8
0.625
38.4
2
3
10
54
小试牛刀
6.判断下面两种量成什么比例关系,并说明理由。
(1)时间一定,织布的总米数和每小时织布的米数。
(2)分子一定,分母和分数值。
(3)打同一份稿件,打字的速度和打字所用的时间。
成正比例关系,因为织布的总米数÷每小时织布的米数=时间(一定)。
成反比例关系,因为分母×分数值=分子(一定)。
成反比例关系,因为打字的速度×打字所用的时间=稿件的总字数(一定)。
课堂小结
归纳总结:
反比例的意义:
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
判断两个量是否成反比例关系的基本步骤:
1. 首先判断两个量是否是相关联的量。
2. 然后再看两个量的积是否为定值。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
