【班海】2022-2023春季人教新版 六下 第一单元 1.负数【优质课件】
文档属性
| 名称 | 【班海】2022-2023春季人教新版 六下 第一单元 1.负数【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
负 数
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
01 课前导入
03 学以致用
02 新课精讲
04 课堂小结
01
课前导入
情景导入
下面是中央气象台2022年1月21日下午发布的六个城市的气温预报(2022年1月21日20时—2022年1月22日20时)。
这些温度怎么读呢?
02
新课精讲
探索新知
探究点 1
相反意义的量
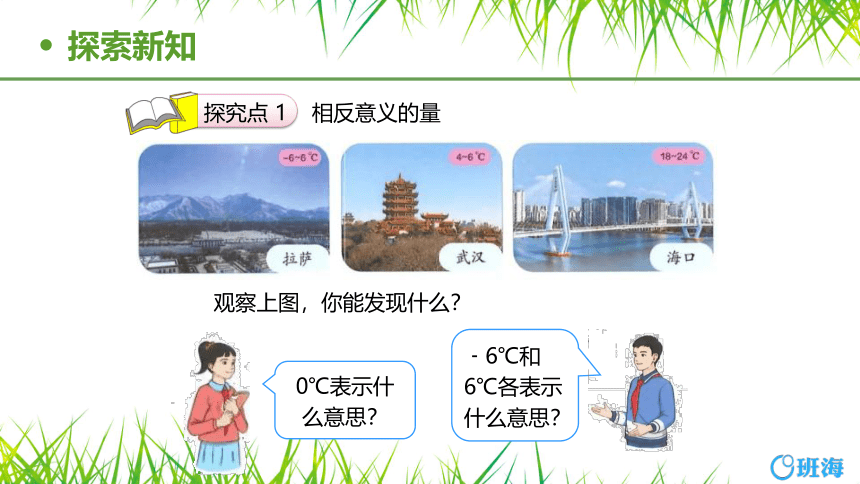
观察上图,你能发现什么?
0℃表示什么意思?
﹣6℃和6℃各表示什么意思?
探索新知
你是怎样知道的?
除了在温度计中有正、负数,生活中消费账单中也有。
探索新知
“-500.00”“+500.00” 正好相反,一个是存入,一个是支出。
“﹣500.00”表示支出500元。
“+500.00”表示存入500元。
为了表示一对具有相反意义的量,如零上温度和零下温度、收入和支出,需要使用正负数。
探索新知
探究点 2
正负数的认识及读写
自学提示:
1. 什么是正数?正数如何去读、写?
2. 什么是负数?负数如何去读、写?
3. 0是正数还是负数?
探索新知
像+3,+500,+4.7, ,这样的数,我们把它们叫做正数,读作“正”,前面的+号也可以省略不写,“正”字也可以省略不读。
探索新知
像- 3,- 500,- 4.7, 等,这样的数,我们把它叫做负数。负号不能省略。负数的读法是:先读“负”,再读数。
0既不是正数也不是负数,它是正数和负数的分界点。
探索新知
你还在什么地方见过负数?
说一说:
探索新知
探究点 3
在直线上表示正数、0和负数
上图中的四个同学以大树为起点,分别向东、西两个相反的方向走。如何在一条直线上表示它们行走的距离和方向呢?
探索新知
(1)从图中你能知道哪些信息?要解决的问题是什么?
(3)要求:请你先独立完成,然后在小组内交流。
(2)你能试着在一条直线上表示他们行走后的情况吗?
温馨提示:
探索新知
正数、负数的意义
为表相反意义量,正数负数来代言。
正负两数分界点,0的作用在中间。
直线两边无限延,就像正负在两边。
典型例题
1.温度越低越冷,-3℃和-18℃那个温度低?
-18℃低
典型例题
2.读出下列各数,并指出哪些是正数,哪些是负数。
-7读作负七;2.5读作二点五;+ 读作正五分之四;0读作零;
-5.2读作负五点二;- 读作负三分之一;+41读作正四十一。
正数:2.5,+ ,+41
负数:-7,-5.2,-
典型例题
3.在直线上表示下列各数。
-4
1
-2
2.5
-0.5
1.5
典型例题
4.某商店1月份营业额为100万元,2月份营业额为130万元,比1月份增长( )%。3月份营业额为90万元,比1月份减少( )% ,称为负增长。也可记为增长-10%。4月份营业额为95万元,比1月份增长( )% 。5月份营业额为100万元,与1月份持平,增长率为( )% ,也称为零增长。
30
10
-5
0
典型例题
5.下列说法正确的是( )。
A.0是正数,不是负数
B.0既不是正数,也不是负数
C.0既是正数,也是负数
D.不是正数的数一定是负数,不是负数的数一定是正数
B
典型例题
6.电梯从1层上升到4层,又从4层下降到1层,然后上升到5层,再下降到1层,照样子请你把这个过程记录下来。
-3
电梯从2层上升到7层,然后下降3层,现在电梯在几层?
+4
-4
7-3=4(层)
03
学以致用
小试牛刀
1.填空。
(1)在-2、 、+3、0、-1.5、48、-0.27中,正数有( ),
负数有( )。
(2)2016年1月1日北京市的最高气温是零上7 ℃,记作( ),
最低气温是零下4 ℃,记作( )。
(3)如果气温下降3 ℃,记作-3 ℃,那么气温上升6 ℃,记作( ),-4 ℃表示( )。
-2、-1.5、-0.27
7 ℃(或+7 ℃)
-4 ℃
6 ℃(或+6 ℃)
下降4 ℃
小试牛刀
2.判断。(对的画“√”,错的画“×”)
(1)带“+”号的数是正数,带“-”号的数是负数。( )
(2)任意一个正数,前面加上“-”号,就是一个负数。( )
(3)大于0的数是正数。( )
(4)一个数不是正数,就是负数。( )
(5)0 ℃就是没有温度。( )
√
×
√
×
×
小试牛刀
3.填空。
(1)如果一家超市3月份盈利4.5万元,记作+4.5万元,四月份亏损4500元,记作( )。
(2)树上一只蜗牛,向上爬5 m,记作+5 m,那么-4 m表示( )。
(3)一种桶装奶粉的标准净重为500 g,质检工作人员为了解这种奶粉每桶的净重与标准的误差,把净重508 g记为+8 g,那么净重495 g就记为( )g。
-4500元
向下爬4 m
-5
小试牛刀
4.选择。(将正确答案的字母填在括号里)
(1)下列不是具有相反意义的量的是( )。
A.浪费1 t水与节约1 t水 B.电梯上升4层与下降3层
C.身高增加2 cm和体重减少2 kg D.增加5 g和减少2 g
(2)如果温泉河的水位升高0.8 m时的水位变化记作+0.8 m,那么水位下降0.5 m时的水位变化记作( )。
A.0 m B.0.5 m C.-0.8 m D.-0.5 m
C
D
小试牛刀
5.读出下面各数。
-20 读作( )
+0.98 读作( )
6.写出下列各数。
负零点三八 写作( )
正三分之一 写作( )
负二十
正零点九八
-0.38
小试牛刀
7.填空。
(1)在直线上,0左边的数都是( ),它们都比0( );所有的( )都在0的右边,它们都比0( )。
(2)在带有正负数的直线上,-1在-8的( )边。
(3)一条鲸鱼现在的位置是-200 m,若它再下潜50 m,则此时所在的位置是( ),再往上游100 m,则此时的位置是( )。
负数
小
正数
大
右
-250 m
-150 m
小试牛刀
8.写出A、B、C、D、E点表示的数。
-9
-4
-1
3
6
9.解决问题。
如果把一个人先向西走40 m记作-40 m,那么这个人又走+55 m是什么意思?这时他距离出发点有多少米?请在下面的直线上表示出来。
向东走55 m。 距离出发点15 m。 图略。
04
课堂小结
归纳总结:
正负数的认识:
为了表示一对具有相反意义的量,如零上温度和零下温度、收入和支出,需要使用正负数。
正负数的表示:
1. 用有正数和负数的直线可以表示距离和相反的方向。
2. 所有的正、负数都可以在直线上找到它的位置。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
负 数
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
01 课前导入
03 学以致用
02 新课精讲
04 课堂小结
01
课前导入
情景导入
下面是中央气象台2022年1月21日下午发布的六个城市的气温预报(2022年1月21日20时—2022年1月22日20时)。
这些温度怎么读呢?
02
新课精讲
探索新知
探究点 1
相反意义的量
观察上图,你能发现什么?
0℃表示什么意思?
﹣6℃和6℃各表示什么意思?
探索新知
你是怎样知道的?
除了在温度计中有正、负数,生活中消费账单中也有。
探索新知
“-500.00”“+500.00” 正好相反,一个是存入,一个是支出。
“﹣500.00”表示支出500元。
“+500.00”表示存入500元。
为了表示一对具有相反意义的量,如零上温度和零下温度、收入和支出,需要使用正负数。
探索新知
探究点 2
正负数的认识及读写
自学提示:
1. 什么是正数?正数如何去读、写?
2. 什么是负数?负数如何去读、写?
3. 0是正数还是负数?
探索新知
像+3,+500,+4.7, ,这样的数,我们把它们叫做正数,读作“正”,前面的+号也可以省略不写,“正”字也可以省略不读。
探索新知
像- 3,- 500,- 4.7, 等,这样的数,我们把它叫做负数。负号不能省略。负数的读法是:先读“负”,再读数。
0既不是正数也不是负数,它是正数和负数的分界点。
探索新知
你还在什么地方见过负数?
说一说:
探索新知
探究点 3
在直线上表示正数、0和负数
上图中的四个同学以大树为起点,分别向东、西两个相反的方向走。如何在一条直线上表示它们行走的距离和方向呢?
探索新知
(1)从图中你能知道哪些信息?要解决的问题是什么?
(3)要求:请你先独立完成,然后在小组内交流。
(2)你能试着在一条直线上表示他们行走后的情况吗?
温馨提示:
探索新知
正数、负数的意义
为表相反意义量,正数负数来代言。
正负两数分界点,0的作用在中间。
直线两边无限延,就像正负在两边。
典型例题
1.温度越低越冷,-3℃和-18℃那个温度低?
-18℃低
典型例题
2.读出下列各数,并指出哪些是正数,哪些是负数。
-7读作负七;2.5读作二点五;+ 读作正五分之四;0读作零;
-5.2读作负五点二;- 读作负三分之一;+41读作正四十一。
正数:2.5,+ ,+41
负数:-7,-5.2,-
典型例题
3.在直线上表示下列各数。
-4
1
-2
2.5
-0.5
1.5
典型例题
4.某商店1月份营业额为100万元,2月份营业额为130万元,比1月份增长( )%。3月份营业额为90万元,比1月份减少( )% ,称为负增长。也可记为增长-10%。4月份营业额为95万元,比1月份增长( )% 。5月份营业额为100万元,与1月份持平,增长率为( )% ,也称为零增长。
30
10
-5
0
典型例题
5.下列说法正确的是( )。
A.0是正数,不是负数
B.0既不是正数,也不是负数
C.0既是正数,也是负数
D.不是正数的数一定是负数,不是负数的数一定是正数
B
典型例题
6.电梯从1层上升到4层,又从4层下降到1层,然后上升到5层,再下降到1层,照样子请你把这个过程记录下来。
-3
电梯从2层上升到7层,然后下降3层,现在电梯在几层?
+4
-4
7-3=4(层)
03
学以致用
小试牛刀
1.填空。
(1)在-2、 、+3、0、-1.5、48、-0.27中,正数有( ),
负数有( )。
(2)2016年1月1日北京市的最高气温是零上7 ℃,记作( ),
最低气温是零下4 ℃,记作( )。
(3)如果气温下降3 ℃,记作-3 ℃,那么气温上升6 ℃,记作( ),-4 ℃表示( )。
-2、-1.5、-0.27
7 ℃(或+7 ℃)
-4 ℃
6 ℃(或+6 ℃)
下降4 ℃
小试牛刀
2.判断。(对的画“√”,错的画“×”)
(1)带“+”号的数是正数,带“-”号的数是负数。( )
(2)任意一个正数,前面加上“-”号,就是一个负数。( )
(3)大于0的数是正数。( )
(4)一个数不是正数,就是负数。( )
(5)0 ℃就是没有温度。( )
√
×
√
×
×
小试牛刀
3.填空。
(1)如果一家超市3月份盈利4.5万元,记作+4.5万元,四月份亏损4500元,记作( )。
(2)树上一只蜗牛,向上爬5 m,记作+5 m,那么-4 m表示( )。
(3)一种桶装奶粉的标准净重为500 g,质检工作人员为了解这种奶粉每桶的净重与标准的误差,把净重508 g记为+8 g,那么净重495 g就记为( )g。
-4500元
向下爬4 m
-5
小试牛刀
4.选择。(将正确答案的字母填在括号里)
(1)下列不是具有相反意义的量的是( )。
A.浪费1 t水与节约1 t水 B.电梯上升4层与下降3层
C.身高增加2 cm和体重减少2 kg D.增加5 g和减少2 g
(2)如果温泉河的水位升高0.8 m时的水位变化记作+0.8 m,那么水位下降0.5 m时的水位变化记作( )。
A.0 m B.0.5 m C.-0.8 m D.-0.5 m
C
D
小试牛刀
5.读出下面各数。
-20 读作( )
+0.98 读作( )
6.写出下列各数。
负零点三八 写作( )
正三分之一 写作( )
负二十
正零点九八
-0.38
小试牛刀
7.填空。
(1)在直线上,0左边的数都是( ),它们都比0( );所有的( )都在0的右边,它们都比0( )。
(2)在带有正负数的直线上,-1在-8的( )边。
(3)一条鲸鱼现在的位置是-200 m,若它再下潜50 m,则此时所在的位置是( ),再往上游100 m,则此时的位置是( )。
负数
小
正数
大
右
-250 m
-150 m
小试牛刀
8.写出A、B、C、D、E点表示的数。
-9
-4
-1
3
6
9.解决问题。
如果把一个人先向西走40 m记作-40 m,那么这个人又走+55 m是什么意思?这时他距离出发点有多少米?请在下面的直线上表示出来。
向东走55 m。 距离出发点15 m。 图略。
04
课堂小结
归纳总结:
正负数的认识:
为了表示一对具有相反意义的量,如零上温度和零下温度、收入和支出,需要使用正负数。
正负数的表示:
1. 用有正数和负数的直线可以表示距离和相反的方向。
2. 所有的正、负数都可以在直线上找到它的位置。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
