2013-2014学年度八年级数学下第二十章数据的分析单元测试题(含答案)
文档属性
| 名称 | 2013-2014学年度八年级数学下第二十章数据的分析单元测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 72.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-13 00:08:57 | ||
图片预览


文档简介
2013-2014学年度八年级数学下
第二十章《数据的分析》检测题
考试时间:120分钟 满分:120分
选择题(每小题3分,共30分)
我省某市五月份第二周连续七天的空气质量指数为:111,96,47,68,70,77,105,则这七天空气质量指数的平均数是( )
A.71.8 B.77 C.82 D.95.7
2.已知一组数据为:-1,0,4,x,6,15,且这组数据的中位数为5,那么这组数据的众数为( )
A.4 B.5 C.5.5 D.6
3.中百商场对上周女装的销售情况进行了统计1,销售情况如表所示:
颜色 黄色 绿色 白色 紫色 红色
数量(件) 100 180 220 80 550
经理决定本周进女装时要多进一些红色的,可用来解释这一现象的统计知识是( )
A.平均数 B.中位数 C.众数 D.方差
4.下列数据是2013年3月7日6点公布的中国六大城市的空气污染指数情况:
城市 北京 合肥 南京 哈尔滨 成都 南昌
污染指数 342 163 165 45 227 163
则这组数据的中位数和众数分别是( )
A.164和163 B.105和163 C.105和164 D.163和164
5.为了了解某小区居民的用水情况,随机抽查了10户家庭月用水量,结果如下表:
月用水量(吨) 4 5 6 9
户数 3 4 2 1
则关于这10户家庭的月用水量,下列说法错误的是( )
A.中位数是5吨 B.极差是3吨 C.平均数是5.3吨 D.众数是5吨
6.甲、乙、丙、丁四位选手10次射击成绩的平均数都是8环,众数和方差如下表:
选手 甲 乙 丙 丁
众数(环) 9 8 8 10
方差() 0.035 0.015 0.025 0.27
则这四人中水平发挥最稳定的是( )
A.甲 B.乙 C.丙 D.丁
7.下列说法中:①样本的方差越小,波动越小,说明样本的稳定性越好;②一组数据的众数只有一个;③一组数据的中位数一定是这组数据中的某一个数据;④数据3,3,3,3,2,5中的众数为4;⑤一组数据的方差一定是正数。其中正确的个数是( )
A.0 B.1 C.2 D.4
8.下列说法中正确的是( )
A.中位数是一组数据中最中间的一个数
B.8,9,9,10,10,11这组数据的众数是9
C.如果,,,…,的平均数是,那么(-)+(-)+…+(-)=0
D.一组数据的方差是这组数据的极差的平方
9.若一组数据,,…,的方差是5,则一组新数据2,2,…,2的方差是( )
A.5 B.10 C.20 D.50
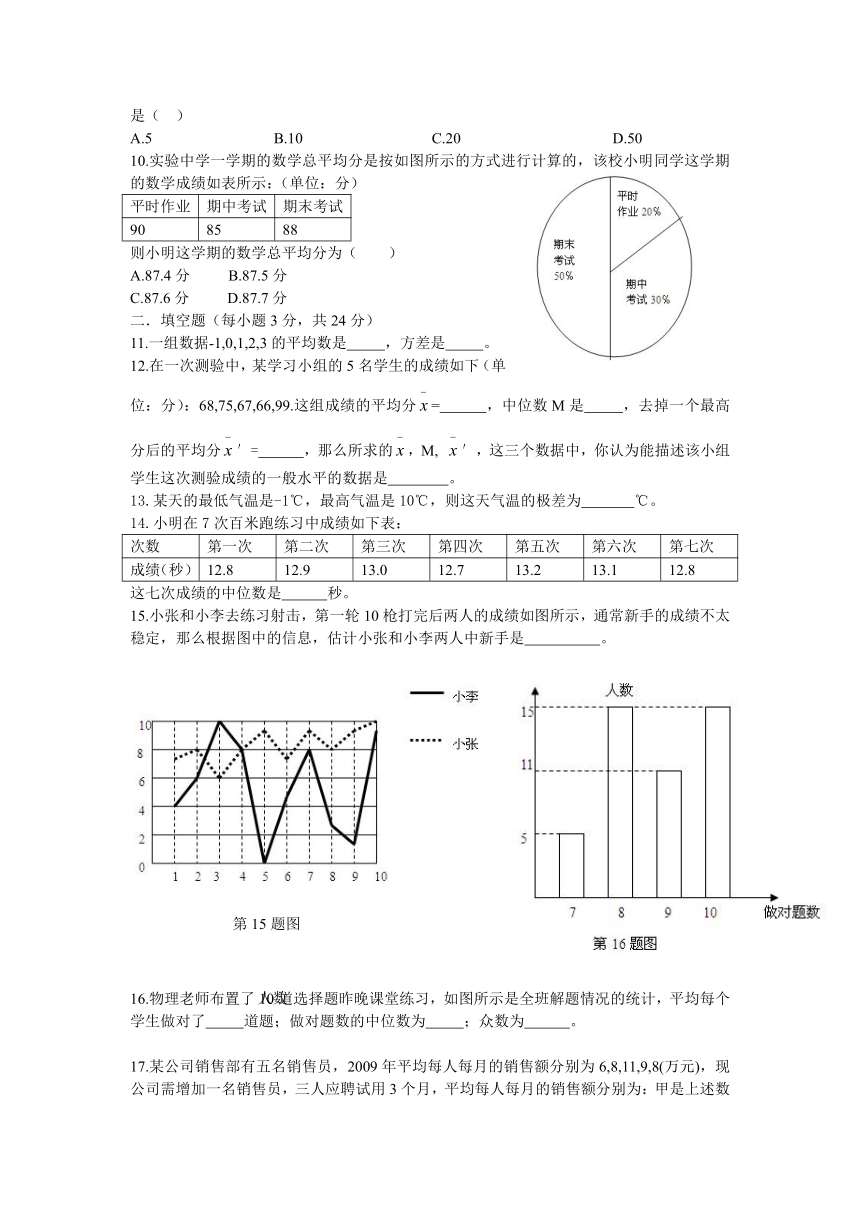
10.实验中学一学期的数学总平均分是按如图所示的方式进行计算的,该校小明同学这学期的数学成绩如表所示:(单位:分)
平时作业 期中考试 期末考试
90 85 88
则小明这学期的数学总平均分为( )
A.87.4分 B.87.5分
C.87.6分 D.87.7分
二.填空题(每小题3分,共24分)
11.一组数据-1,0,1,2,3的平均数是 ,方差是 。
12.在一次测验中,某学习小组的5名学生的成绩如下(单位:分):68,75,67,66,99.这组成绩的平均分= ,中位数M是 ,去掉一个最高分后的平均分′= ,那么所求的,M, ′,这三个数据中,你认为能描述该小组学生这次测验成绩的一般水平的数据是 。
13.某天的最低气温是-1℃,最高气温是10℃,则这天气温的极差为 ℃。
14.小明在7次百米跑练习中成绩如下表:
次数 第一次 第二次 第三次 第四次 第五次 第六次 第七次
成绩(秒) 12.8 12.9 13.0 12.7 13.2 13.1 12.8
这七次成绩的中位数是 秒。
15.小张和小李去练习射击,第一轮10枪打完后两人的成绩如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小张和小李两人中新手是 。
16.物理老师布置了10道选择题昨晚课堂练习,如图所示是全班解题情况的统计,平均每个学生做对了 道题;做对题数的中位数为 ;众数为 。
17.某公司销售部有五名销售员,2009年平均每人每月的销售额分别为6,8,11,9,8(万元),现公司需增加一名销售员,三人应聘试用3个月,平均每人每月的销售额分别为:甲是上述数据的平均数,乙是中位数,丙是众数,最后录用三人中平均月销售额最高的人是 。
18.王老板为了与顾客签订合同,对自己鱼塘中鱼的总重量进行评估,第一次捞出100条,称得重量为184㎏,并将每条鱼做好记号后放入水中,当它们完全混合于鱼群之后,又捞出200条,称得重量为416㎏,且带有记号的鱼有20条,根据以上数据提供的信息,王老板鱼塘中估计有鱼 条,共重约 ㎏。
三.解答题(共66分)
19.(12分)某工厂有220名员工,财务科要了解员工收入情况。现在抽查了10名员工的本月收入,结果如下:(单位:元)
1660 1540 1510 1670 1620 1580 1600 1620 1620 1580
(1)全厂员工的月平均收入是多少?
(2)平均每名员工的年薪是多少?
(3)财务科本月应准备多少钱发工资?
(4)一名本月收入为1570元的员工的收入水平如何?
20.(12分)下表是某校九年级(1)班20名学生某次数学测验的成绩统计表:
成绩(分) 60 70 80 90 100
人数(个) 1 5 x y 2
若这20名学生成绩的平均分为82,求x和y的值;
在(1)的条件下,设这20名学生本次测验成绩的众数为a,中位数为b,求a和b的值。
21.(14分)王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%,现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示。
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
22.(14分)某公司招聘职员,对甲乙两位候选人进行面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人 面试 笔试
形体 口才 专业水平 创新能力
甲 86 90 96 92
乙 92 88 95 93
若公司根据经营性质和岗位要求认为:形体、口才专业水平、创新能力按照5:5:4:6的比确定,请计算甲乙两人各自的平均成绩,看看谁将被录取?
若公司根据经营性质和岗位要求认为:面试中形体占5%、口才占30%,笔试中专业水平占35%、创新能力占30%,那么你认为该公司应该录取谁?
23.(14分)为了解某品牌A、B两种型号冰箱的销售情况,王明对其专卖店开业以来连续七个月的销售情况进行了统计,并将得到的数据制成了如下的统计表:(单位:台)
表一
月份 一月 二月 三月 四月 五月 六月 七月
A型销售量 10 14 17 16 13 14 14
B型销售量 6 10 14 15 16 17 20
表二
平均数 中位数 方差
A型销售量 14
B型销售量 14 18.6
完成表二;(结果精确到0.1)
请你根据其个月的销售情况绘制折线统计图,并根据折线统计图的变化趋势,对专卖店今后的进货情况提出建议。(字数控制在20~50字)
第二十章《数据的分析》检测题参考答案
选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C A B B B C B C
填空题:
11.1,2 12.75,68,69,M或 13.12 14.12.9 15.小李 16.8.78;9;8和10
17.甲 18.1000;2000
三.解答题
19.解:(1)=(1660+1540+…+1620)=1600元
∴全厂员工的月平均收入约1600元
(2)由(1)得这个厂220名员工的月平均收入是1600元,
∴平均每名员工的年薪是1600×12=19200元
由(1)得: 1600×220=352000元
中位数是1610元
∴全厂员工本月收入的中位数是1610元
∵1570<1610
∴一名本月收入为1570元的员工的收入可能是中下水平
20.解:(1)根据题意得,
解这个方程组得x=5,y=7
(2)a=90,b=80
21.解:(1)=40(千克);=40(千克);总产量为40×100×98%×2=7840(千克)
(2)=+++=38,
=+++=24
∴>,即乙山上的杨梅产量较稳定。
22.解:(1)形体、口才专业水平、创新能力按照5:5:4:6的比确定,
则甲的平均成绩为=90.8
乙的平均成绩为=91.9
∴乙的成绩比甲的高。
∴应该录取乙。
(2)面试中形体占5%、口才占30%,笔试中专业水平占35%、创新能力占30%,则甲的平均成绩为86×5%+90×30%+96×35%+92×30%=92.5,乙的平均成绩为92×5%+88×30%+95×35%+93×30%=92.15.
∴甲的成绩比乙的高
∴应该录取甲。
23.解:(1)A型销售量;平均数14;方差14.3 B型销售量;中位数15
(2)图略。建议多进B型,从折线变化趋势看,B比A更有潜力,因为B型一直呈上升趋势。
第15题图
人数
第二十章《数据的分析》检测题
考试时间:120分钟 满分:120分
选择题(每小题3分,共30分)
我省某市五月份第二周连续七天的空气质量指数为:111,96,47,68,70,77,105,则这七天空气质量指数的平均数是( )
A.71.8 B.77 C.82 D.95.7
2.已知一组数据为:-1,0,4,x,6,15,且这组数据的中位数为5,那么这组数据的众数为( )
A.4 B.5 C.5.5 D.6
3.中百商场对上周女装的销售情况进行了统计1,销售情况如表所示:
颜色 黄色 绿色 白色 紫色 红色
数量(件) 100 180 220 80 550
经理决定本周进女装时要多进一些红色的,可用来解释这一现象的统计知识是( )
A.平均数 B.中位数 C.众数 D.方差
4.下列数据是2013年3月7日6点公布的中国六大城市的空气污染指数情况:
城市 北京 合肥 南京 哈尔滨 成都 南昌
污染指数 342 163 165 45 227 163
则这组数据的中位数和众数分别是( )
A.164和163 B.105和163 C.105和164 D.163和164
5.为了了解某小区居民的用水情况,随机抽查了10户家庭月用水量,结果如下表:
月用水量(吨) 4 5 6 9
户数 3 4 2 1
则关于这10户家庭的月用水量,下列说法错误的是( )
A.中位数是5吨 B.极差是3吨 C.平均数是5.3吨 D.众数是5吨
6.甲、乙、丙、丁四位选手10次射击成绩的平均数都是8环,众数和方差如下表:
选手 甲 乙 丙 丁
众数(环) 9 8 8 10
方差() 0.035 0.015 0.025 0.27
则这四人中水平发挥最稳定的是( )
A.甲 B.乙 C.丙 D.丁
7.下列说法中:①样本的方差越小,波动越小,说明样本的稳定性越好;②一组数据的众数只有一个;③一组数据的中位数一定是这组数据中的某一个数据;④数据3,3,3,3,2,5中的众数为4;⑤一组数据的方差一定是正数。其中正确的个数是( )
A.0 B.1 C.2 D.4
8.下列说法中正确的是( )
A.中位数是一组数据中最中间的一个数
B.8,9,9,10,10,11这组数据的众数是9
C.如果,,,…,的平均数是,那么(-)+(-)+…+(-)=0
D.一组数据的方差是这组数据的极差的平方
9.若一组数据,,…,的方差是5,则一组新数据2,2,…,2的方差是( )
A.5 B.10 C.20 D.50
10.实验中学一学期的数学总平均分是按如图所示的方式进行计算的,该校小明同学这学期的数学成绩如表所示:(单位:分)
平时作业 期中考试 期末考试
90 85 88
则小明这学期的数学总平均分为( )
A.87.4分 B.87.5分
C.87.6分 D.87.7分
二.填空题(每小题3分,共24分)
11.一组数据-1,0,1,2,3的平均数是 ,方差是 。
12.在一次测验中,某学习小组的5名学生的成绩如下(单位:分):68,75,67,66,99.这组成绩的平均分= ,中位数M是 ,去掉一个最高分后的平均分′= ,那么所求的,M, ′,这三个数据中,你认为能描述该小组学生这次测验成绩的一般水平的数据是 。
13.某天的最低气温是-1℃,最高气温是10℃,则这天气温的极差为 ℃。
14.小明在7次百米跑练习中成绩如下表:
次数 第一次 第二次 第三次 第四次 第五次 第六次 第七次
成绩(秒) 12.8 12.9 13.0 12.7 13.2 13.1 12.8
这七次成绩的中位数是 秒。
15.小张和小李去练习射击,第一轮10枪打完后两人的成绩如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小张和小李两人中新手是 。
16.物理老师布置了10道选择题昨晚课堂练习,如图所示是全班解题情况的统计,平均每个学生做对了 道题;做对题数的中位数为 ;众数为 。
17.某公司销售部有五名销售员,2009年平均每人每月的销售额分别为6,8,11,9,8(万元),现公司需增加一名销售员,三人应聘试用3个月,平均每人每月的销售额分别为:甲是上述数据的平均数,乙是中位数,丙是众数,最后录用三人中平均月销售额最高的人是 。
18.王老板为了与顾客签订合同,对自己鱼塘中鱼的总重量进行评估,第一次捞出100条,称得重量为184㎏,并将每条鱼做好记号后放入水中,当它们完全混合于鱼群之后,又捞出200条,称得重量为416㎏,且带有记号的鱼有20条,根据以上数据提供的信息,王老板鱼塘中估计有鱼 条,共重约 ㎏。
三.解答题(共66分)
19.(12分)某工厂有220名员工,财务科要了解员工收入情况。现在抽查了10名员工的本月收入,结果如下:(单位:元)
1660 1540 1510 1670 1620 1580 1600 1620 1620 1580
(1)全厂员工的月平均收入是多少?
(2)平均每名员工的年薪是多少?
(3)财务科本月应准备多少钱发工资?
(4)一名本月收入为1570元的员工的收入水平如何?
20.(12分)下表是某校九年级(1)班20名学生某次数学测验的成绩统计表:
成绩(分) 60 70 80 90 100
人数(个) 1 5 x y 2
若这20名学生成绩的平均分为82,求x和y的值;
在(1)的条件下,设这20名学生本次测验成绩的众数为a,中位数为b,求a和b的值。
21.(14分)王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%,现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示。
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
22.(14分)某公司招聘职员,对甲乙两位候选人进行面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人 面试 笔试
形体 口才 专业水平 创新能力
甲 86 90 96 92
乙 92 88 95 93
若公司根据经营性质和岗位要求认为:形体、口才专业水平、创新能力按照5:5:4:6的比确定,请计算甲乙两人各自的平均成绩,看看谁将被录取?
若公司根据经营性质和岗位要求认为:面试中形体占5%、口才占30%,笔试中专业水平占35%、创新能力占30%,那么你认为该公司应该录取谁?
23.(14分)为了解某品牌A、B两种型号冰箱的销售情况,王明对其专卖店开业以来连续七个月的销售情况进行了统计,并将得到的数据制成了如下的统计表:(单位:台)
表一
月份 一月 二月 三月 四月 五月 六月 七月
A型销售量 10 14 17 16 13 14 14
B型销售量 6 10 14 15 16 17 20
表二
平均数 中位数 方差
A型销售量 14
B型销售量 14 18.6
完成表二;(结果精确到0.1)
请你根据其个月的销售情况绘制折线统计图,并根据折线统计图的变化趋势,对专卖店今后的进货情况提出建议。(字数控制在20~50字)
第二十章《数据的分析》检测题参考答案
选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C A B B B C B C
填空题:
11.1,2 12.75,68,69,M或 13.12 14.12.9 15.小李 16.8.78;9;8和10
17.甲 18.1000;2000
三.解答题
19.解:(1)=(1660+1540+…+1620)=1600元
∴全厂员工的月平均收入约1600元
(2)由(1)得这个厂220名员工的月平均收入是1600元,
∴平均每名员工的年薪是1600×12=19200元
由(1)得: 1600×220=352000元
中位数是1610元
∴全厂员工本月收入的中位数是1610元
∵1570<1610
∴一名本月收入为1570元的员工的收入可能是中下水平
20.解:(1)根据题意得,
解这个方程组得x=5,y=7
(2)a=90,b=80
21.解:(1)=40(千克);=40(千克);总产量为40×100×98%×2=7840(千克)
(2)=+++=38,
=+++=24
∴>,即乙山上的杨梅产量较稳定。
22.解:(1)形体、口才专业水平、创新能力按照5:5:4:6的比确定,
则甲的平均成绩为=90.8
乙的平均成绩为=91.9
∴乙的成绩比甲的高。
∴应该录取乙。
(2)面试中形体占5%、口才占30%,笔试中专业水平占35%、创新能力占30%,则甲的平均成绩为86×5%+90×30%+96×35%+92×30%=92.5,乙的平均成绩为92×5%+88×30%+95×35%+93×30%=92.15.
∴甲的成绩比乙的高
∴应该录取甲。
23.解:(1)A型销售量;平均数14;方差14.3 B型销售量;中位数15
(2)图略。建议多进B型,从折线变化趋势看,B比A更有潜力,因为B型一直呈上升趋势。
第15题图
人数
