2022-2023学年高一下学期数学北师大版(2019)必修第二册《6.1基本立体图形》课件(共29张PPT)
文档属性
| 名称 | 2022-2023学年高一下学期数学北师大版(2019)必修第二册《6.1基本立体图形》课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 723.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
6.1 基本立体图形
新知探究
问题1 想一想平面几何的研究对象、内容、基本元素是什么?
平面几何的研究对象是平面图形.
平面几何的基本元素是点、线.
平面几何的研究内容是点、线的位置关系、图形的画法、相关计算及应用.
问题2 空间几何体的几何元素是什么?
空间几何体的几何元素有点、线(直线和曲线)、面(平面和曲面).
新知探究
问题3 生活中粉笔、电线杆等给我们以直线的形象;黑板、平整的操场、桌面、平静的湖面等则给我们以平面的印象,试举出更多例子.那么,平面的含义是什么呢?
教室的地面,天花板等,
但是几何里的平面是无限延展的.
几何里所说的“平面”就是从这样的一些物体中抽象出来的.
追问 通常用什么图形来表示平面?
一般用平行四边形来表示平面.
新知探究
问题4 阅读教材第193页,教材中给出的这些几何体各有什么特点?哪些几何体可以归为一类?
由平面多边形围成的,称为多面体,这些多边形称为多面体的面,
由曲面围成的称为旋转体.
相邻的面的公共边称为多面体的棱,棱与棱的公共点称为多面体的顶点.
新知探究
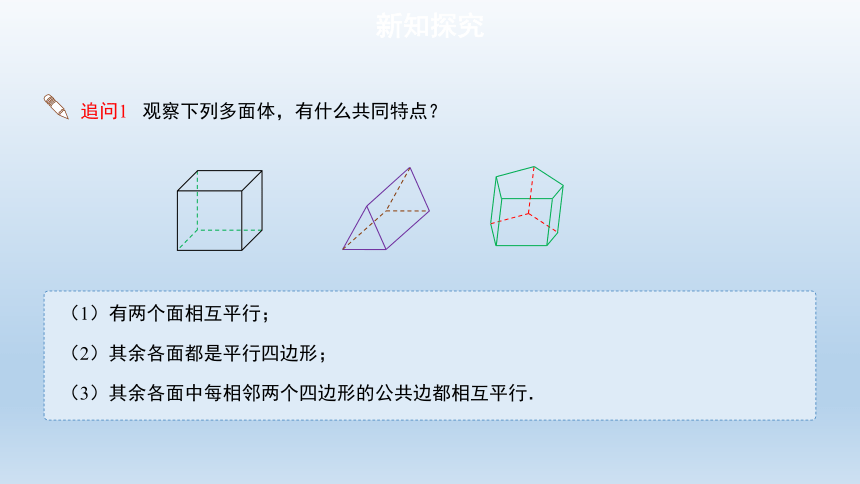
追问1 观察下列多面体,有什么共同特点?
(1)有两个面相互平行;
(2)其余各面都是平行四边形;
(3)其余各面中每相邻两个四边形的公共边都相互平行.
新知探究
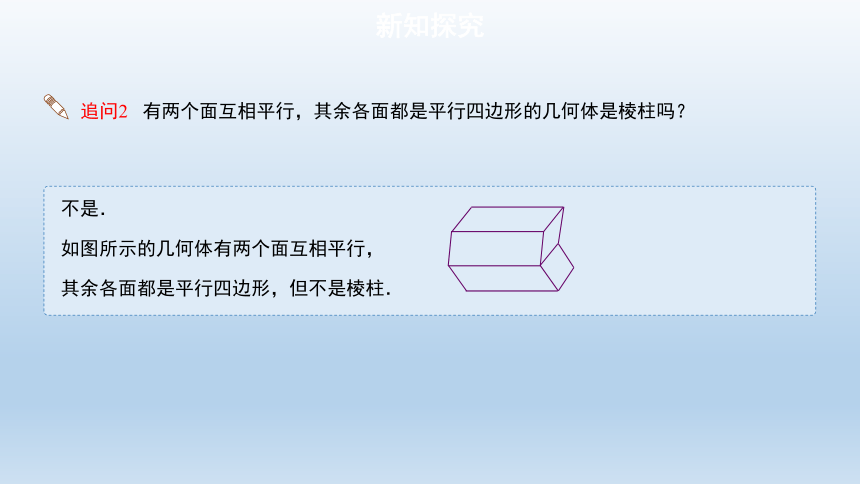
追问2 有两个面互相平行,其余各面都是平行四边形的几何体是棱柱吗?
不是.
如图所示的几何体有两个面互相平行,
其余各面都是平行四边形,但不是棱柱.
新知探究
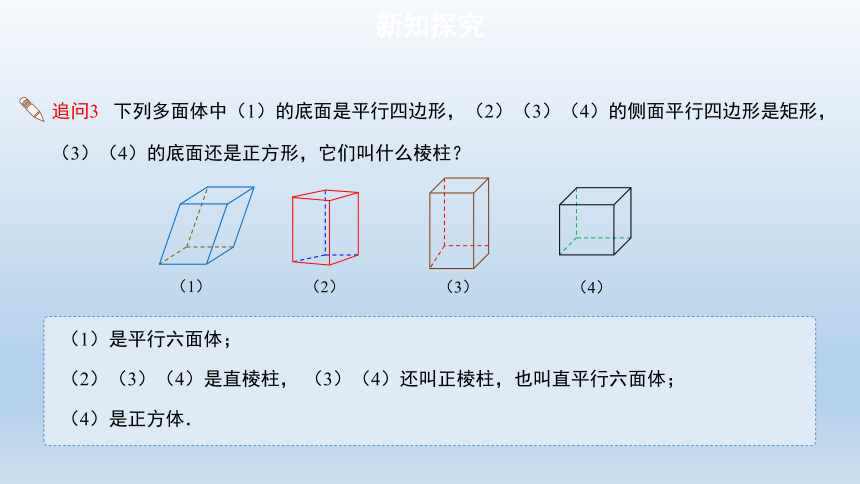
追问3 下列多面体中(1)的底面是平行四边形,(2)(3)(4)的侧面平行四边形是矩形,
(3)(4)的底面还是正方形,它们叫什么棱柱?
(1)是平行六面体;
(2)(3)(4)是直棱柱,
(4)是正方体.
(1)
(2)
(3)
(4)
(3)(4)还叫正棱柱,也叫直平行六面体;
新知探究
有一个面是多边形,其余各面是有一个公共顶点的三角形围成.
三棱锥也叫四面体.
问题5 阅读教材,你发现金字塔、法国卢浮宫玻璃金字塔及帐篷的结构特征有什么共同点?三棱锥还可以叫什么?,
新知探究
追问1 底面是正多边形的棱锥是正棱锥吗?为什么?
不是.
正棱锥的底面不仅是正多边形;
而且它的顶点在过底面中心且与底面垂直的直线上.
新知探究
追问2 棱台是多面体吗?棱台有哪些作为棱台集合的特征性质?如何利用棱台的特征性质给
棱台下一个定义?
棱台是多面体,棱台的各棱的延长线交于一点.
定义:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分.
A
B
C
D
A′
B′
C′
D′
新知探究
问题6 你能归说出棱柱、棱锥、棱台表示、结构特征、侧棱、侧面、底面的定义吗?
名称 棱柱 棱锥 棱台
图形
表示
结构 特征
侧棱
侧面
底面
棱柱AC′或
棱柱ABCDE-A′B′C′D′E′
棱锥S-AC或
棱锥S-ABCDE
棱台AC′或
棱台ABCD-A′B′C′D′
用一个平行于棱锥底面的平面去截
棱锥,底面与截面之间的部分
两个面互相平行,其余各面都
是四边形,并且每相邻两个四
边形的公共边都互相平行
有一个面是多边形,其余各面是有
一个公共顶点的三角形
平行且相等
相交于一点,但不一定相等
延长线交于一点,但不一定相等
平行四边形
三角形
梯形
平行且全等的多边形
多边形
平行且边数相等的多边形
新知探究
半圆弧旋转形成一个球面,圆弧旋转形成的也是一个球面,
它们围成的空间几何体都是球.
问题7 如图,把半圆绕其直径所在的直线旋转一周,半圆弧旋转形成什么图形?如果是把整个的圆绕其一条直径所在的直线旋转半周,圆弧旋转形成什么图形?它们各自围成什么空间几何体?
新知探究
追问1 球有什么性质?
(1)球面上所有的点到球心距离等于球的半径;
(2)用任何一个平面去截球面,得到的截面是圆,
其中过球心的平面截球面得到的圆的半径最大,等于球的半径.
半径
球心
O
新知探究
追问2 什么是旋转面、旋转体?
一条平面曲线绕着它所在的平面内的一条定直线旋转一周所形成的曲面称为旋转面;
封闭的旋转面围成的几何体称为旋转体.
轴
新知探究
边BC,DA旋转各形成一个圆面,边CD旋转形成一个曲面,
它们共同围成一个圆柱.
问题8 如图,矩形ABCD绕其边AB所在直线旋转一周,其余三边BC,CD,DA旋转各形成什么图形?共同围成什么空间几何体?
A
B
C
D
追问 圆柱的母线有多少条?它们之间有什么关系?
圆柱的母线有无数条;
它们之间相互平行.
新知探究
边BC旋转形成一个圆面,边AB旋转形成一个曲面,
它们共同围成一个圆锥.
问题9 如图,Rt△ABC绕其一直角边AC所在的直线旋转一周,其余两边BC,AB旋转各形成什么图形?它们共同围成什么空间几何体?
C
B
A
新知探究
追问1 如图,用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是什么空间几
何体?
圆台.
O
O′
新知探究
追问2 你能写出球、圆柱、圆锥、圆台的结构特征吗?
名称 定义 图形表示 相关概念
球
圆柱 圆锥 圆台
以半圆的直径所在的直线为旋转轴,将半圆旋转所形成的曲面叫作球面.球面所围成的几何体叫作球体,简称球.
球心:半圆的圆心;
球的半径:连接球心和球面上任意一点的线段;
球的直径:连接球面上两点并且过球心的线段.
分别以矩形的一边、直角三角形的一条直角边、直角梯形垂直于底边的腰所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体分别叫作圆柱、圆锥、圆台.
高:在旋转轴上这条边的长度;
底面:垂直于旋转轴的边旋转而成的圆面;
侧面:不垂直于旋转轴的边旋转而成的曲面;
母线:不垂直于旋转轴的边旋转,无论转到
什么位置,都叫作侧面的母线.
初步应用
例1 下列关于棱锥、棱台的说法:
①用一个平面去截棱锥,底面和截面之间的部分组成的几何体叫棱台;
②棱柱的侧面一定是平行四边形;
③棱锥的侧面只能是三角形;
④由四个面围成的封闭图形只能是三棱锥;
⑤棱锥被平面截成的两部分不可能都是棱锥.
其中正确说法的序号是________.
初步应用
例1 下列关于棱锥、棱台的说法:
①用一个平面去截棱锥,底面和截面之间的部分组成的几何体叫棱台;
②棱柱的侧面一定是平行四边形;
③棱锥的侧面只能是三角形;
④由四个面围成的封闭图形只能是三棱锥;
①错误,若平面不与棱锥底面平行,用这个平面去截棱锥,棱锥底面和截面之间的部分不是棱台;
②正确,棱柱的侧面是对边平行的四边形;
③正确,由棱锥的定义知棱锥的侧面只能是三角形;
④正确,由四个面围成的封闭图形只能是三棱锥;
初步应用
例1 下列关于棱锥、棱台的说法:
①用一个平面去截棱锥,底面和截面之间的部分组成的几何体叫棱台;
②棱柱的侧面一定是平行四边形;
③棱锥的侧面只能是三角形;
④由四个面围成的封闭图形只能是三棱锥;
⑤棱锥被平面截成的两部分不可能都是棱锥.
其中正确说法的序号是________.
⑤错误,如图所示四棱锥被平面截成的两部分都是棱锥.
综上,②③④正确.
②③④
初步应用
把圆柱的侧面沿AB剪开,然后展开成为平面图形——矩形,如图所示,
连接AB′,则AB′即为蚂蚁爬行的最短距离.
∵AA′为底面圆的周长,
∴AB′=,
例2 如图所示,有一个底面半径为1,高为2的圆柱体,在A点处有一只蚂蚁,现在这只蚂蚁要围绕圆柱表面一周且由A点爬到B点,问蚂蚁爬行的最短距离是多少?
A
B
∴AA′=2π×1=2π.又AB=A′B′=2,
即蚂蚁爬行的最短距离为.
课堂练习
练习:教科书第198页练习1,2,3,4,5,6 .
归纳小结
(1)理解多面体应注意什么?
(2)如图是三个几何体的侧面展开图,
请问各是什么几何体?
问题3 本节课收获了哪些知识,请你从以下几方面总结:
(3)通过本节课的学习,你还有收获了哪些研究经验?
(1)对于多面体而言,应仔细区分底面与侧面分别是怎样的多边形,多边形公共边有无平行关系.
多面体的底面与其放置位置无关,对于柱体应仔细区分.
(2)①为五棱柱;②为五棱锥;③为三棱台.
(3)研究经验是:…….
作业布置
作业:教科书第198页,A组第1,2,3,4题.
1
目标检测
①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;
给出下列命题:
②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线;
③在圆台的上、下两底面圆周上各取一点,则这两点的连线是圆台的母线;
④圆柱的任意两条母线所在的直线是互相平行的.
其中正确的是( )
A.①②
B.②③
C.①③
D.②④
解析:依据圆柱、圆锥和圆台的定义及母线的性质可知,②④正确,①③错误.
D
2
目标检测
D
如图,已知长方体ABCD-A1B1C1D1,过BC和AD分别作一个平面交底面A1B1C1D1于EF,PQ,则在长方体被分成的三个几何体中,棱柱的个数是( )
A.0
B.1
C.2
D.3
解析:该长方体被分成的三个几何体都是棱柱,
分别为三棱柱AA1P-DD1Q,三棱柱BB1E-CC1F和四棱柱ABEP-DCFQ.
3
目标检测
若一个正棱锥有6个顶点,所有侧棱长的和为20cm,则每条侧棱的长为________ cm.
解析:依题意,正棱锥有6个顶点,则该正棱锥为正五棱锥,
所以每条侧棱长为 =4cm.
4
4
目标检测
圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于392 cm2,母线与轴的夹角是45°,求这个圆台的高、母线长和两底面半径.
解析:圆台的轴截面如图所示.
设圆台上、下底面半径分别为xcm,3xcm,延长AA1交OO1的延长线于S.
在Rt△SOA中,∠ASO=45°,∠SAO=45°,
则圆台的高OO1=14cm,母线长l=OO1=cm.
两底面的半径分别为7cm,21cm.
∴SO=AO=3x,∴OO1=2x,
又S轴截面= (6x+2x)·2x=392,∴x=7,
6.1 基本立体图形
新知探究
问题1 想一想平面几何的研究对象、内容、基本元素是什么?
平面几何的研究对象是平面图形.
平面几何的基本元素是点、线.
平面几何的研究内容是点、线的位置关系、图形的画法、相关计算及应用.
问题2 空间几何体的几何元素是什么?
空间几何体的几何元素有点、线(直线和曲线)、面(平面和曲面).
新知探究
问题3 生活中粉笔、电线杆等给我们以直线的形象;黑板、平整的操场、桌面、平静的湖面等则给我们以平面的印象,试举出更多例子.那么,平面的含义是什么呢?
教室的地面,天花板等,
但是几何里的平面是无限延展的.
几何里所说的“平面”就是从这样的一些物体中抽象出来的.
追问 通常用什么图形来表示平面?
一般用平行四边形来表示平面.
新知探究
问题4 阅读教材第193页,教材中给出的这些几何体各有什么特点?哪些几何体可以归为一类?
由平面多边形围成的,称为多面体,这些多边形称为多面体的面,
由曲面围成的称为旋转体.
相邻的面的公共边称为多面体的棱,棱与棱的公共点称为多面体的顶点.
新知探究
追问1 观察下列多面体,有什么共同特点?
(1)有两个面相互平行;
(2)其余各面都是平行四边形;
(3)其余各面中每相邻两个四边形的公共边都相互平行.
新知探究
追问2 有两个面互相平行,其余各面都是平行四边形的几何体是棱柱吗?
不是.
如图所示的几何体有两个面互相平行,
其余各面都是平行四边形,但不是棱柱.
新知探究
追问3 下列多面体中(1)的底面是平行四边形,(2)(3)(4)的侧面平行四边形是矩形,
(3)(4)的底面还是正方形,它们叫什么棱柱?
(1)是平行六面体;
(2)(3)(4)是直棱柱,
(4)是正方体.
(1)
(2)
(3)
(4)
(3)(4)还叫正棱柱,也叫直平行六面体;
新知探究
有一个面是多边形,其余各面是有一个公共顶点的三角形围成.
三棱锥也叫四面体.
问题5 阅读教材,你发现金字塔、法国卢浮宫玻璃金字塔及帐篷的结构特征有什么共同点?三棱锥还可以叫什么?,
新知探究
追问1 底面是正多边形的棱锥是正棱锥吗?为什么?
不是.
正棱锥的底面不仅是正多边形;
而且它的顶点在过底面中心且与底面垂直的直线上.
新知探究
追问2 棱台是多面体吗?棱台有哪些作为棱台集合的特征性质?如何利用棱台的特征性质给
棱台下一个定义?
棱台是多面体,棱台的各棱的延长线交于一点.
定义:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分.
A
B
C
D
A′
B′
C′
D′
新知探究
问题6 你能归说出棱柱、棱锥、棱台表示、结构特征、侧棱、侧面、底面的定义吗?
名称 棱柱 棱锥 棱台
图形
表示
结构 特征
侧棱
侧面
底面
棱柱AC′或
棱柱ABCDE-A′B′C′D′E′
棱锥S-AC或
棱锥S-ABCDE
棱台AC′或
棱台ABCD-A′B′C′D′
用一个平行于棱锥底面的平面去截
棱锥,底面与截面之间的部分
两个面互相平行,其余各面都
是四边形,并且每相邻两个四
边形的公共边都互相平行
有一个面是多边形,其余各面是有
一个公共顶点的三角形
平行且相等
相交于一点,但不一定相等
延长线交于一点,但不一定相等
平行四边形
三角形
梯形
平行且全等的多边形
多边形
平行且边数相等的多边形
新知探究
半圆弧旋转形成一个球面,圆弧旋转形成的也是一个球面,
它们围成的空间几何体都是球.
问题7 如图,把半圆绕其直径所在的直线旋转一周,半圆弧旋转形成什么图形?如果是把整个的圆绕其一条直径所在的直线旋转半周,圆弧旋转形成什么图形?它们各自围成什么空间几何体?
新知探究
追问1 球有什么性质?
(1)球面上所有的点到球心距离等于球的半径;
(2)用任何一个平面去截球面,得到的截面是圆,
其中过球心的平面截球面得到的圆的半径最大,等于球的半径.
半径
球心
O
新知探究
追问2 什么是旋转面、旋转体?
一条平面曲线绕着它所在的平面内的一条定直线旋转一周所形成的曲面称为旋转面;
封闭的旋转面围成的几何体称为旋转体.
轴
新知探究
边BC,DA旋转各形成一个圆面,边CD旋转形成一个曲面,
它们共同围成一个圆柱.
问题8 如图,矩形ABCD绕其边AB所在直线旋转一周,其余三边BC,CD,DA旋转各形成什么图形?共同围成什么空间几何体?
A
B
C
D
追问 圆柱的母线有多少条?它们之间有什么关系?
圆柱的母线有无数条;
它们之间相互平行.
新知探究
边BC旋转形成一个圆面,边AB旋转形成一个曲面,
它们共同围成一个圆锥.
问题9 如图,Rt△ABC绕其一直角边AC所在的直线旋转一周,其余两边BC,AB旋转各形成什么图形?它们共同围成什么空间几何体?
C
B
A
新知探究
追问1 如图,用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是什么空间几
何体?
圆台.
O
O′
新知探究
追问2 你能写出球、圆柱、圆锥、圆台的结构特征吗?
名称 定义 图形表示 相关概念
球
圆柱 圆锥 圆台
以半圆的直径所在的直线为旋转轴,将半圆旋转所形成的曲面叫作球面.球面所围成的几何体叫作球体,简称球.
球心:半圆的圆心;
球的半径:连接球心和球面上任意一点的线段;
球的直径:连接球面上两点并且过球心的线段.
分别以矩形的一边、直角三角形的一条直角边、直角梯形垂直于底边的腰所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体分别叫作圆柱、圆锥、圆台.
高:在旋转轴上这条边的长度;
底面:垂直于旋转轴的边旋转而成的圆面;
侧面:不垂直于旋转轴的边旋转而成的曲面;
母线:不垂直于旋转轴的边旋转,无论转到
什么位置,都叫作侧面的母线.
初步应用
例1 下列关于棱锥、棱台的说法:
①用一个平面去截棱锥,底面和截面之间的部分组成的几何体叫棱台;
②棱柱的侧面一定是平行四边形;
③棱锥的侧面只能是三角形;
④由四个面围成的封闭图形只能是三棱锥;
⑤棱锥被平面截成的两部分不可能都是棱锥.
其中正确说法的序号是________.
初步应用
例1 下列关于棱锥、棱台的说法:
①用一个平面去截棱锥,底面和截面之间的部分组成的几何体叫棱台;
②棱柱的侧面一定是平行四边形;
③棱锥的侧面只能是三角形;
④由四个面围成的封闭图形只能是三棱锥;
①错误,若平面不与棱锥底面平行,用这个平面去截棱锥,棱锥底面和截面之间的部分不是棱台;
②正确,棱柱的侧面是对边平行的四边形;
③正确,由棱锥的定义知棱锥的侧面只能是三角形;
④正确,由四个面围成的封闭图形只能是三棱锥;
初步应用
例1 下列关于棱锥、棱台的说法:
①用一个平面去截棱锥,底面和截面之间的部分组成的几何体叫棱台;
②棱柱的侧面一定是平行四边形;
③棱锥的侧面只能是三角形;
④由四个面围成的封闭图形只能是三棱锥;
⑤棱锥被平面截成的两部分不可能都是棱锥.
其中正确说法的序号是________.
⑤错误,如图所示四棱锥被平面截成的两部分都是棱锥.
综上,②③④正确.
②③④
初步应用
把圆柱的侧面沿AB剪开,然后展开成为平面图形——矩形,如图所示,
连接AB′,则AB′即为蚂蚁爬行的最短距离.
∵AA′为底面圆的周长,
∴AB′=,
例2 如图所示,有一个底面半径为1,高为2的圆柱体,在A点处有一只蚂蚁,现在这只蚂蚁要围绕圆柱表面一周且由A点爬到B点,问蚂蚁爬行的最短距离是多少?
A
B
∴AA′=2π×1=2π.又AB=A′B′=2,
即蚂蚁爬行的最短距离为.
课堂练习
练习:教科书第198页练习1,2,3,4,5,6 .
归纳小结
(1)理解多面体应注意什么?
(2)如图是三个几何体的侧面展开图,
请问各是什么几何体?
问题3 本节课收获了哪些知识,请你从以下几方面总结:
(3)通过本节课的学习,你还有收获了哪些研究经验?
(1)对于多面体而言,应仔细区分底面与侧面分别是怎样的多边形,多边形公共边有无平行关系.
多面体的底面与其放置位置无关,对于柱体应仔细区分.
(2)①为五棱柱;②为五棱锥;③为三棱台.
(3)研究经验是:…….
作业布置
作业:教科书第198页,A组第1,2,3,4题.
1
目标检测
①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;
给出下列命题:
②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线;
③在圆台的上、下两底面圆周上各取一点,则这两点的连线是圆台的母线;
④圆柱的任意两条母线所在的直线是互相平行的.
其中正确的是( )
A.①②
B.②③
C.①③
D.②④
解析:依据圆柱、圆锥和圆台的定义及母线的性质可知,②④正确,①③错误.
D
2
目标检测
D
如图,已知长方体ABCD-A1B1C1D1,过BC和AD分别作一个平面交底面A1B1C1D1于EF,PQ,则在长方体被分成的三个几何体中,棱柱的个数是( )
A.0
B.1
C.2
D.3
解析:该长方体被分成的三个几何体都是棱柱,
分别为三棱柱AA1P-DD1Q,三棱柱BB1E-CC1F和四棱柱ABEP-DCFQ.
3
目标检测
若一个正棱锥有6个顶点,所有侧棱长的和为20cm,则每条侧棱的长为________ cm.
解析:依题意,正棱锥有6个顶点,则该正棱锥为正五棱锥,
所以每条侧棱长为 =4cm.
4
4
目标检测
圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于392 cm2,母线与轴的夹角是45°,求这个圆台的高、母线长和两底面半径.
解析:圆台的轴截面如图所示.
设圆台上、下底面半径分别为xcm,3xcm,延长AA1交OO1的延长线于S.
在Rt△SOA中,∠ASO=45°,∠SAO=45°,
则圆台的高OO1=14cm,母线长l=OO1=cm.
两底面的半径分别为7cm,21cm.
∴SO=AO=3x,∴OO1=2x,
又S轴截面= (6x+2x)·2x=392,∴x=7,
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
