2022-2023学年高一下学期数学北师大版(2019)必修第二册《6.3空间点、直线、平面之间的位置关系》第2课时课件(共25张PPT)
文档属性
| 名称 | 2022-2023学年高一下学期数学北师大版(2019)必修第二册《6.3空间点、直线、平面之间的位置关系》第2课时课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 380.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
6.3 空间点、直线、平面之间的位置关系
第2课时
导入新课
问题1 在初中,我们曾学过“平行于同一直线的两条直线平行”,这一事实可以拓展到空间吗?
可以.
a
b
新知探究
AB∥C1D1.
问题2 观察长方体ABCD-A1B1C1D1,显然AB∥CD,CD∥C1D1,则AB与C1D1有何位置关系?
A
B
C
D
C1
D1
B1
A1
新知探究
问题3 你能把上述结论推广到空间吗?如何用语言和符号表示所得的结论?
能,
用符号a∥b且b∥c a∥c.
平行于同一直线的两条直线平行,
问题4 我们知道直线与直线有两种位置关系:相交和不相交,不相交一定平行吗?
不一定,
如问题2中的BD1与AC就不相交,但它们也不平行.
新知探究
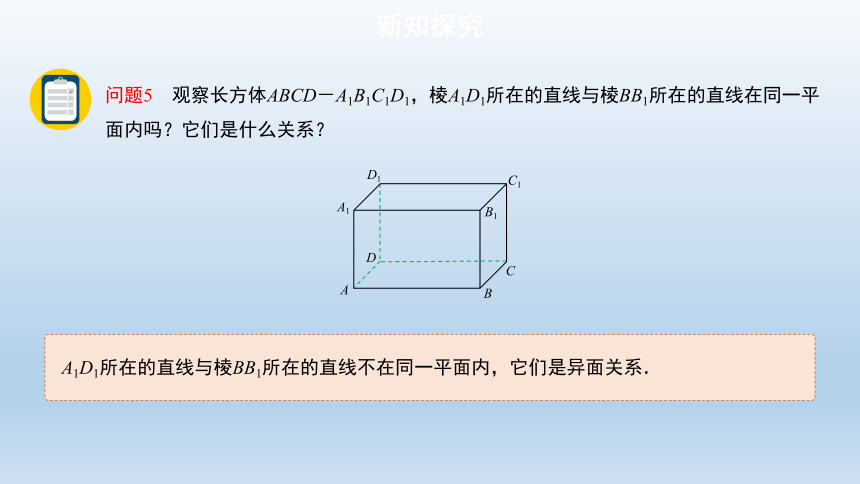
问题5 观察长方体ABCD-A1B1C1D1,棱A1D1所在的直线与棱BB1所在的直线在同一平面内吗?它们是什么关系?
A
B
C
D
C1
D1
B1
A1
A1D1所在的直线与棱BB1所在的直线不在同一平面内,它们是异面关系.
新知探究
追问1 分别在两个平面内的两条直线是否一定异面?
不一定.它们可能异面,可能相交,也可能平行.
追问2 你能归纳出异面直线的概念吗?
异面直线:不同在任何一个平面内(不共面)的两条直线叫异面直线.
新知探究
问题6 你能说出空间两条直线的位置关系吗?
两直线的位置关系有:
(2)异面直线:不共面的两条直线且没有公共点.
(1)共面直线
相交直线:在同一平面内有且有一个公共点,
平行直线:在同一平面内没有公共点.
新知探究
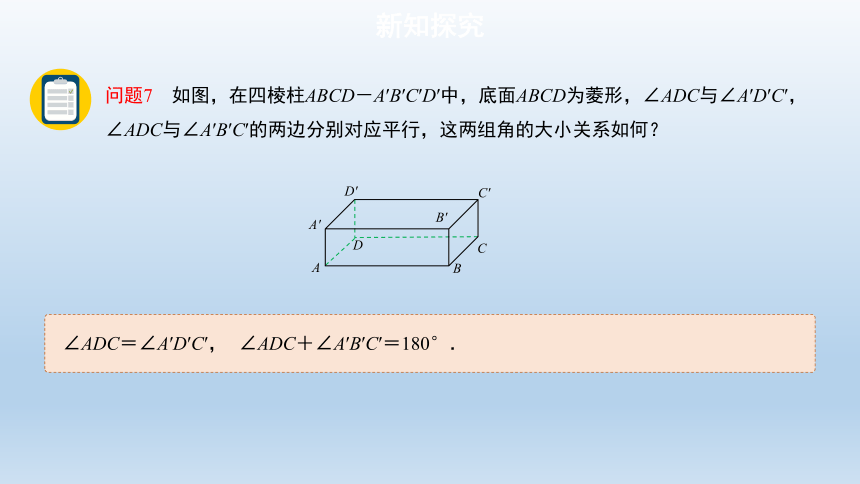
∠ADC=∠A′D′C′,
∠ADC+∠A′B′C′=180°.
问题7 如图,在四棱柱ABCD-A′B′C′D′中,底面ABCD为菱形,∠ADC与∠A′D′C′,∠ADC与∠A′B′C′的两边分别对应平行,这两组角的大小关系如何?
A
B
C
D
C′
D′
B′
A′
新知探究
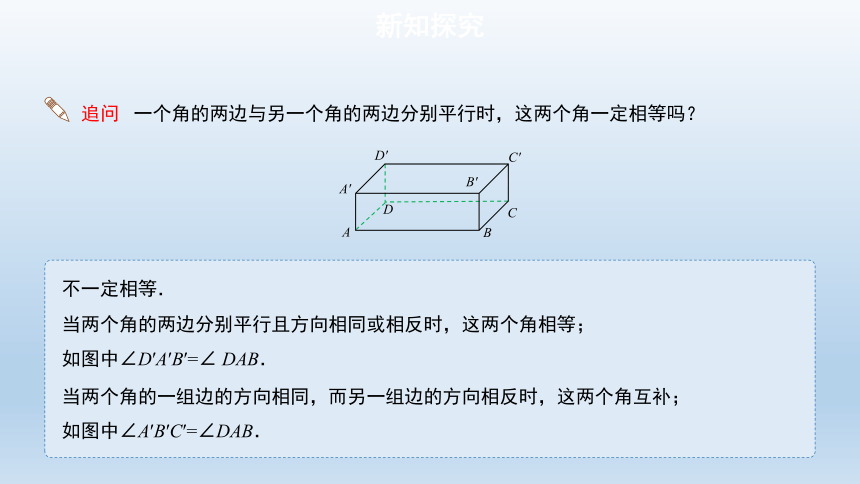
追问 一个角的两边与另一个角的两边分别平行时,这两个角一定相等吗?
不一定相等.
当两个角的两边分别平行且方向相同或相反时,这两个角相等;
如图中∠D′A′B′=∠ DAB.
当两个角的一组边的方向相同,而另一组边的方向相反时,这两个角互补;
如图中∠A′B′C′=∠DAB.
A
B
C
D
C′
D′
B′
A′
新知探究
问题8 平面内两条直线相交成4个角,其中不大于90°称为它们的夹角,那么两平行直线所成的角是多少?
两平行直线所成的角是0°或180°.
追问1 异面直线所成的角如何度量?范围是什么?
a
b
θ
O
a′
a′
b′
O
θ
(1)已知两条异面直线a,b,过空间任选一点O,过
的锐角(或直角),就是异面直线a,b所成的角.
点O分别作a′∥a,b′∥b,则a′,b′这两条相交直线所成
(2)异面直线所成的角的取值范围为.
新知探究
追问2 当异面直线所成角为 时,a与b位置关系是什么?如何表示?
a与b互相垂直,记作a⊥b.
B1
C
C1
A
B
D
A1
D1
a
b
初步应用
例1 四个顶点不在同一平面内的四边形称为空间四边形,如图所示,在空间四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
A
H
D
G
C
F
B
E
证明:连接BD.
因为FG是△CBD的中位线,
所以EH∥FG,EH=FG,
所以FG∥BD,且,
同理EH∥BD,且,
所以四边形EFGH是平行四边形.
初步应用
例2 如图所示,已知正方体ABCD-A1B1C1D1的棱长为a.
(1)正方体的哪些棱所在的直线与直线BC1是异面直线?
(2)求异面直线AA1与BC所成的角;
(3)求异面直线BC1与AC所成的角.
A1
B1
C1
D1
C
D
B
A
解析:(1)A1A,A1B1,A1D1,DA,DC,DD1;
(2)将AA1平移到BB1; BB1与BB1的夹角为90°,故AA1与BC所成的角为90°;
(3)连接A1B,A1C1,因为AA1//CC1且AA1=CC1,所以四边形AA1C1C为平行四边形.
故AC//A1C1且AC=A1C1,故∠A1C1B为异面直线BC1与AC所成的角.
在 A1C1B中,因为A1B=BC1=A1C1=,所以∠A1C1B=60°.
初步应用
例3 如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠BMC=∠B1M1C1.
A
B
C
D
C1
D1
B1
A1
M1
M
证明: (1)∵ABCD-A1B1C1D1为正方体,
又M,M1分别为棱AD,A1D1的中点,
∴四边形AMM1A1为平行四边形,
又AA1=BB1且AA1∥BB1,
∴四边形BB1M1M为平行四边形.
∴AD A1D1,
∴AM A1M1,
∴MM1 AA1.
∴MM1 BB1,
初步应用
例3 如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠BMC=∠B1M1C1.
A
B
C
D
C1
D1
B1
A1
M1
M
(2)法一:由(1)知四边形 BB1M1M 为平行四边形,
所以 B1M1∥BM.
同理,可得四边形 CC1M1M 为平行四边形,
由平面几何知识,可知∠BMC 和 ∠B1M1C1 都是锐角,
所以 C1M1∥CM.
故 ∠BMC=∠B1M1C1.
初步应用
例3 如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠BMC=∠B1M1C1.
A
B
C
D
C1
D1
B1
A1
M1
M
法二:由(1)可知四边形 BB1M1M 为平行四边形,
∴B1M1=BM.
同理可得四边形CC1M1M为平行四边形,
又∵B1C1=BC,
∴C1M1=CM.
∴△BCM≌△B1C1M1,
∴∠BMC=∠B1M1C1.
归纳小结
问题9 本节课我们学习了基本事实4和等角定理以及异面直线、异面直线所成的角,请你通过下列问题,归纳所学知识.
(1)基本事实4及等角定理的作用是什么?
(2)已知直线a,b是两条异面直线,如何作出这两条异面直线所成的角?
(3)a′与b′所成角的大小与什么有关,与点O的位置有关吗?通常点O取在什么位置?
(1)基本事实4又叫平行线的传递性.
等角定理的主要作用是证明空间两个角相等.
作用主要是证明两条直线平行.
归纳小结
问题9 本节课我们学习了基本事实4和等角定理以及异面直线、异面直线所成的角,请你通过下列问题,归纳所学知识.
(1)基本事实4及等角定理的作用是什么?
(2)已知直线a,b是两条异面直线,如何作出这两条异面直线所成的角?
(3)a′与b′所成角的大小与什么有关,与点O的位置有关吗?通常点O取在什么位置?
(2)如图,在空间中任取一点O,作直线a′∥a,b′∥b,
则两条相交直线 a′,b′ 所成的锐角或直角 θ 即两条异面直线a,b所成的角.
归纳小结
问题9 本节课我们学习了基本事实4和等角定理以及异面直线、异面直线所成的角,请你通过下列问题,归纳所学知识.
(1)基本事实4及等角定理的作用是什么?
(2)已知直线a,b是两条异面直线,如何作出这两条异面直线所成的角?
(3)a′与b′所成角的大小与什么有关,与点O的位置有关吗?通常点O取在什么位置?
(3)a′与b′所成角的大小只由a,b的相互位置确定,
一般情况下为了简便,点O选取在两条直线中的一条直线上.
与点O的选择无关.
作业布置
作业:教科书第215页B组1,2,3.
1
目标检测
B
已知AB∥PQ,BC∥QR,∠ABC=30°,则∠PQR等于( )
A.30°
B.30°或150°
C.150°
D.以上结论都不对
解析:∠ABC的两边与∠PQR的两边分别平行,但方向不能确定是否相同,
∴∠PQR=30°或150°.
2
目标检测
D
若∠AOB=∠A1O1B1且OA∥O1A1,OA与O1A1的方向相同,则下列结论正确的是( )
A.OB∥O1B1且OB与O1B1方向相同
B.OB∥O1B1
C.OB与O1B1不平行
D.OB与O1B1不一定平行
解析:如图,在正方体中,OB与O1B1不平行,
若它们在同一平面内,则OB∥O1B1.
B
B1
O1
A
O
A1
3
目标检测
90°
如图在正方体ABCD-A1B1C1D1中,异面直线B1D与BC1所成的角为________.
A1
B1
C1
D1
C
D
B
A
解析:取CD的中点E,连接B1C交BC1于F,连接EF,则EF∥B1D.
异面直线B1D与BC1所成的角即为EF与BC1所成的锐角或直角,显然EF⊥BC1,
故所求角为90°.
E
F
4
目标检测
如图,在正方体ABCD-A1B1C1D1中,M、N分别是棱CD、CC1的中点,求异面直线A1M与DN所成的角的大小.
A
B
C
D
C1
D1
B1
A1
K
解析:取CN 的中点K,连接A1K,MK,
所以∠A1MK或其补角为异面直线 A1M 与 DN 所成的角,连接 A1C1,AM.
设正方体棱长为4,
A1M==6,
∴A1M2+MK2=A1K2,
∴∠A1MK=90°.
则MK为△CDN的中位线,所以MK∥DN,
则A1K=
M
N
6.3 空间点、直线、平面之间的位置关系
第2课时
导入新课
问题1 在初中,我们曾学过“平行于同一直线的两条直线平行”,这一事实可以拓展到空间吗?
可以.
a
b
新知探究
AB∥C1D1.
问题2 观察长方体ABCD-A1B1C1D1,显然AB∥CD,CD∥C1D1,则AB与C1D1有何位置关系?
A
B
C
D
C1
D1
B1
A1
新知探究
问题3 你能把上述结论推广到空间吗?如何用语言和符号表示所得的结论?
能,
用符号a∥b且b∥c a∥c.
平行于同一直线的两条直线平行,
问题4 我们知道直线与直线有两种位置关系:相交和不相交,不相交一定平行吗?
不一定,
如问题2中的BD1与AC就不相交,但它们也不平行.
新知探究
问题5 观察长方体ABCD-A1B1C1D1,棱A1D1所在的直线与棱BB1所在的直线在同一平面内吗?它们是什么关系?
A
B
C
D
C1
D1
B1
A1
A1D1所在的直线与棱BB1所在的直线不在同一平面内,它们是异面关系.
新知探究
追问1 分别在两个平面内的两条直线是否一定异面?
不一定.它们可能异面,可能相交,也可能平行.
追问2 你能归纳出异面直线的概念吗?
异面直线:不同在任何一个平面内(不共面)的两条直线叫异面直线.
新知探究
问题6 你能说出空间两条直线的位置关系吗?
两直线的位置关系有:
(2)异面直线:不共面的两条直线且没有公共点.
(1)共面直线
相交直线:在同一平面内有且有一个公共点,
平行直线:在同一平面内没有公共点.
新知探究
∠ADC=∠A′D′C′,
∠ADC+∠A′B′C′=180°.
问题7 如图,在四棱柱ABCD-A′B′C′D′中,底面ABCD为菱形,∠ADC与∠A′D′C′,∠ADC与∠A′B′C′的两边分别对应平行,这两组角的大小关系如何?
A
B
C
D
C′
D′
B′
A′
新知探究
追问 一个角的两边与另一个角的两边分别平行时,这两个角一定相等吗?
不一定相等.
当两个角的两边分别平行且方向相同或相反时,这两个角相等;
如图中∠D′A′B′=∠ DAB.
当两个角的一组边的方向相同,而另一组边的方向相反时,这两个角互补;
如图中∠A′B′C′=∠DAB.
A
B
C
D
C′
D′
B′
A′
新知探究
问题8 平面内两条直线相交成4个角,其中不大于90°称为它们的夹角,那么两平行直线所成的角是多少?
两平行直线所成的角是0°或180°.
追问1 异面直线所成的角如何度量?范围是什么?
a
b
θ
O
a′
a′
b′
O
θ
(1)已知两条异面直线a,b,过空间任选一点O,过
的锐角(或直角),就是异面直线a,b所成的角.
点O分别作a′∥a,b′∥b,则a′,b′这两条相交直线所成
(2)异面直线所成的角的取值范围为.
新知探究
追问2 当异面直线所成角为 时,a与b位置关系是什么?如何表示?
a与b互相垂直,记作a⊥b.
B1
C
C1
A
B
D
A1
D1
a
b
初步应用
例1 四个顶点不在同一平面内的四边形称为空间四边形,如图所示,在空间四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
A
H
D
G
C
F
B
E
证明:连接BD.
因为FG是△CBD的中位线,
所以EH∥FG,EH=FG,
所以FG∥BD,且,
同理EH∥BD,且,
所以四边形EFGH是平行四边形.
初步应用
例2 如图所示,已知正方体ABCD-A1B1C1D1的棱长为a.
(1)正方体的哪些棱所在的直线与直线BC1是异面直线?
(2)求异面直线AA1与BC所成的角;
(3)求异面直线BC1与AC所成的角.
A1
B1
C1
D1
C
D
B
A
解析:(1)A1A,A1B1,A1D1,DA,DC,DD1;
(2)将AA1平移到BB1; BB1与BB1的夹角为90°,故AA1与BC所成的角为90°;
(3)连接A1B,A1C1,因为AA1//CC1且AA1=CC1,所以四边形AA1C1C为平行四边形.
故AC//A1C1且AC=A1C1,故∠A1C1B为异面直线BC1与AC所成的角.
在 A1C1B中,因为A1B=BC1=A1C1=,所以∠A1C1B=60°.
初步应用
例3 如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠BMC=∠B1M1C1.
A
B
C
D
C1
D1
B1
A1
M1
M
证明: (1)∵ABCD-A1B1C1D1为正方体,
又M,M1分别为棱AD,A1D1的中点,
∴四边形AMM1A1为平行四边形,
又AA1=BB1且AA1∥BB1,
∴四边形BB1M1M为平行四边形.
∴AD A1D1,
∴AM A1M1,
∴MM1 AA1.
∴MM1 BB1,
初步应用
例3 如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠BMC=∠B1M1C1.
A
B
C
D
C1
D1
B1
A1
M1
M
(2)法一:由(1)知四边形 BB1M1M 为平行四边形,
所以 B1M1∥BM.
同理,可得四边形 CC1M1M 为平行四边形,
由平面几何知识,可知∠BMC 和 ∠B1M1C1 都是锐角,
所以 C1M1∥CM.
故 ∠BMC=∠B1M1C1.
初步应用
例3 如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠BMC=∠B1M1C1.
A
B
C
D
C1
D1
B1
A1
M1
M
法二:由(1)可知四边形 BB1M1M 为平行四边形,
∴B1M1=BM.
同理可得四边形CC1M1M为平行四边形,
又∵B1C1=BC,
∴C1M1=CM.
∴△BCM≌△B1C1M1,
∴∠BMC=∠B1M1C1.
归纳小结
问题9 本节课我们学习了基本事实4和等角定理以及异面直线、异面直线所成的角,请你通过下列问题,归纳所学知识.
(1)基本事实4及等角定理的作用是什么?
(2)已知直线a,b是两条异面直线,如何作出这两条异面直线所成的角?
(3)a′与b′所成角的大小与什么有关,与点O的位置有关吗?通常点O取在什么位置?
(1)基本事实4又叫平行线的传递性.
等角定理的主要作用是证明空间两个角相等.
作用主要是证明两条直线平行.
归纳小结
问题9 本节课我们学习了基本事实4和等角定理以及异面直线、异面直线所成的角,请你通过下列问题,归纳所学知识.
(1)基本事实4及等角定理的作用是什么?
(2)已知直线a,b是两条异面直线,如何作出这两条异面直线所成的角?
(3)a′与b′所成角的大小与什么有关,与点O的位置有关吗?通常点O取在什么位置?
(2)如图,在空间中任取一点O,作直线a′∥a,b′∥b,
则两条相交直线 a′,b′ 所成的锐角或直角 θ 即两条异面直线a,b所成的角.
归纳小结
问题9 本节课我们学习了基本事实4和等角定理以及异面直线、异面直线所成的角,请你通过下列问题,归纳所学知识.
(1)基本事实4及等角定理的作用是什么?
(2)已知直线a,b是两条异面直线,如何作出这两条异面直线所成的角?
(3)a′与b′所成角的大小与什么有关,与点O的位置有关吗?通常点O取在什么位置?
(3)a′与b′所成角的大小只由a,b的相互位置确定,
一般情况下为了简便,点O选取在两条直线中的一条直线上.
与点O的选择无关.
作业布置
作业:教科书第215页B组1,2,3.
1
目标检测
B
已知AB∥PQ,BC∥QR,∠ABC=30°,则∠PQR等于( )
A.30°
B.30°或150°
C.150°
D.以上结论都不对
解析:∠ABC的两边与∠PQR的两边分别平行,但方向不能确定是否相同,
∴∠PQR=30°或150°.
2
目标检测
D
若∠AOB=∠A1O1B1且OA∥O1A1,OA与O1A1的方向相同,则下列结论正确的是( )
A.OB∥O1B1且OB与O1B1方向相同
B.OB∥O1B1
C.OB与O1B1不平行
D.OB与O1B1不一定平行
解析:如图,在正方体中,OB与O1B1不平行,
若它们在同一平面内,则OB∥O1B1.
B
B1
O1
A
O
A1
3
目标检测
90°
如图在正方体ABCD-A1B1C1D1中,异面直线B1D与BC1所成的角为________.
A1
B1
C1
D1
C
D
B
A
解析:取CD的中点E,连接B1C交BC1于F,连接EF,则EF∥B1D.
异面直线B1D与BC1所成的角即为EF与BC1所成的锐角或直角,显然EF⊥BC1,
故所求角为90°.
E
F
4
目标检测
如图,在正方体ABCD-A1B1C1D1中,M、N分别是棱CD、CC1的中点,求异面直线A1M与DN所成的角的大小.
A
B
C
D
C1
D1
B1
A1
K
解析:取CN 的中点K,连接A1K,MK,
所以∠A1MK或其补角为异面直线 A1M 与 DN 所成的角,连接 A1C1,AM.
设正方体棱长为4,
A1M==6,
∴A1M2+MK2=A1K2,
∴∠A1MK=90°.
则MK为△CDN的中位线,所以MK∥DN,
则A1K=
M
N
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
