高中数学北师大版(2019)必修 第二册第六章 立体几何初步【教学课件】《6.3空间点、直线、平面之间的位置关系》第1课时 课件(共25张PPT)
文档属性
| 名称 | 高中数学北师大版(2019)必修 第二册第六章 立体几何初步【教学课件】《6.3空间点、直线、平面之间的位置关系》第1课时 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 352.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 19:34:08 | ||
图片预览







文档简介
(共25张PPT)
6.3 空间点、直线、平面之间的位置关系
第1课时
导入新课
问题1 观察下图中的长方体,它有几个顶点?几条棱?几个面?
A
B
C
D
C1
D1
B1
A1
长方体有8个顶点、12条棱、6个面
追问1 长方体的12条棱中,棱与棱有几种位置关系?
棱与棱的位置关系有:相交,平行,既不平行也不相交.
导入新课
追问2 长方体的12条棱和6个面之间有哪些关系?
棱在平面内,棱所在直线与平面平行,棱所在直线与平面相交.
追问3 6个面之间有哪几种位置关系?
6个面之间的位置关系有平行和相交.
新知探究
问题2 平面α是由点组成的,直线l也是由点组成的,从集合的观点看,点P与直线l有何关系?点P与平面α有何关系?直线l与平面α呢?
点P与直线l的关系:P在l上或P不在l上;
直线 l 与平面α的关系:l在α内、l与α平行、l与α相交.
点P与平面α的关系:P在α内或P不在α内;
P∈l
P∈α
P l
P α
l α
l α
l α
新知探究
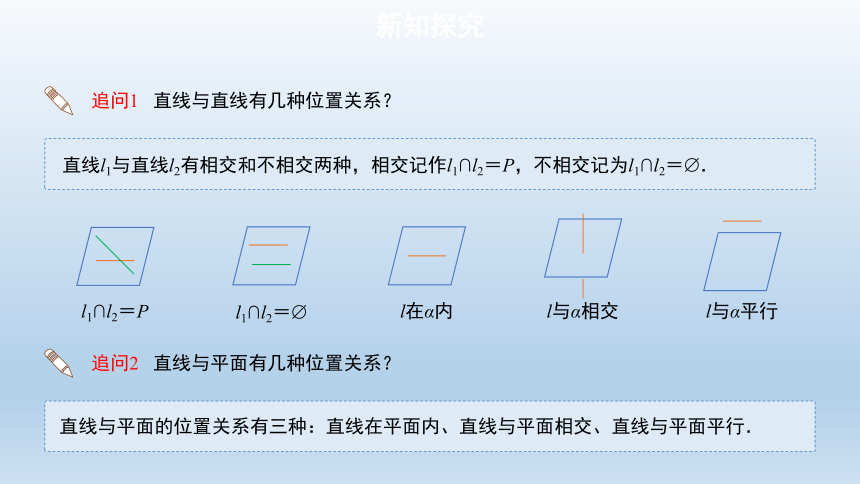
直线l1与直线l2有相交和不相交两种,相交记作l1∩l2=P,不相交记为l1∩l2= .
直线与平面的位置关系有三种:直线在平面内、直线与平面相交、直线与平面平行.
追问2 直线与平面有几种位置关系?
追问1 直线与直线有几种位置关系?
l在α内
l与α相交
l与α平行
l1∩l2=
l1∩l2=P
新知探究
直线l在平面α内,记作 l α;
直线 l 与α平行,记作 l∥α l∩α= .
追问3 直线 l 在平面α内如何表示?直线l与α平行呢?
新知探究
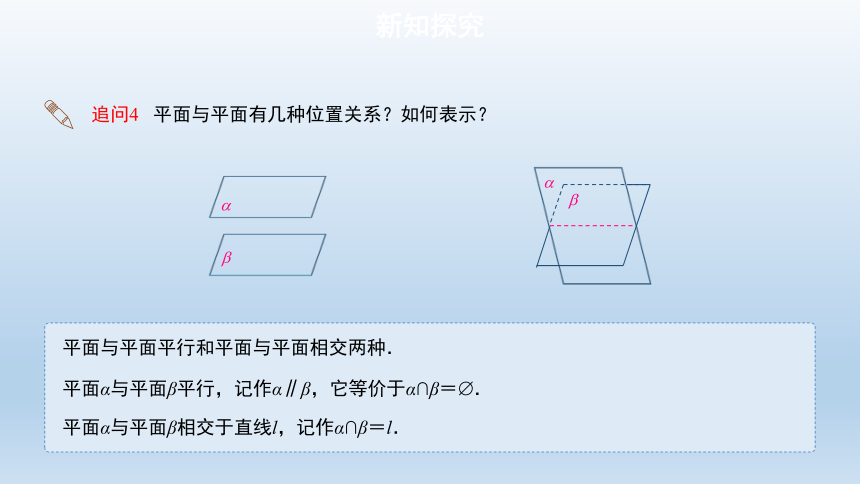
追问4 平面与平面有几种位置关系?如何表示?
平面与平面平行和平面与平面相交两种.
平面α与平面β平行,记作α∥β,它等价于α∩β= .
平面α与平面β相交于直线l,记作α∩β=l.
新知探究
因为不在同一直线上的三点可以确定一个平面.
故三脚架可以牢固地支撑照相机或测量用的平板仪.
不一定.只有经过空间不共线的三点才能确定一个平面.
问题3 生活中常见到这样的现象:三脚架可以牢固地支撑照相机或测量用的平板仪等,请问这是为什么?
追问 经过空间任意三点能确定一个平面吗?
新知探究
问题4 若把直尺边缘上的任意两点放在桌面上,直尺的边缘上的其余点和桌面有何关系?
直尺边缘上的其余点都在桌面上.
追问 如何判断直线在平面内?
因为两点确定一条直线,
所以只要直线上的两点在一个平面内,这条直线就在这个平面内.
新知探究
问题5 下列说法是否正确?并说明理由.
这三个结论都正确,由基本事实1,2可以推证.
(1)一条直线和直线外一点确定一个平面.
(2)两条相交直线确定一个平面.
(3)两条平行直线确定一个平面.
新知探究
问题6 观察正方体ABCD-A1B1C1D1(如图所示),平面ABCD与平面BCC1B1有且只有两个公共点B,C吗?
不是.平面ABCD∩平面BCC1B1=BC.
不可能.因为平面是无限延展的,所以两平面的交线是一条直线.
A
B
C
D
C1
D1
B1
A1
追问 两个平面的交线可能是一条线段吗?
新知探究
问题7 你能叙述基本事实1,2,3吗?
基本事实1:过不在一条直线上的三个点,有且只有一个平面.
基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有过该点的公共直线.
基本事实2:如果一条直线上的两点在一个平面内,那么这条直线在这个平面内
(即直线在平面内).
α
A
B
C
●
●
●
A
B
l
α
●
●
α
β
P
l
新知探究
问题8 由基本事实3,你能得出判断直线共面的什么条件?
基本事实2的推论
推论1:一条直线和直线外一点确定一个平面;
推论2:两条相交直线确定一个平面;
推论3:两条平行直线确定一个平面.
α
B
C
A
●
a
●
●
A
α
B
C
●
●
●
α
C
A
B
●
●
●
a
b
初步应用
例1 用符号表示下列语句,并画出图形.
(1)平面α与β相交于直线l,直线a与α,β分别相交于点A,B;
(2)点A,B在平面α内,直线a与平面α交于点C,点C不在直线AB上.
解析:
(2)用符号表示:A∈α,B∈α,a∩α=C,C AB,如图2.
(1)用符号表示:α∩β=l,a∩α=A,a∩β=B,如图1.
图1
图2
例2 证明:两两相交且不共点的三条直线在同一平面内.
初步应用
已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.
求证:直线l1,l2,l3在同一平面内.
解析:法一 ∵l1∩l2=A,∴l1和l2确定一个平面α.
∵l2∩l3=B,∴B∈l2又l2 α,∴B∈α.
同理可证C∈α,又B∈l3,C∈l3,∴l3 α.
∴直线l1,l2,l3在同一平面内.
例2 证明:两两相交且不共点的三条直线在同一平面内.
初步应用
解析:法二 ∵l1∩l2=A,∴l1,l2确定一个平面α.
∵l2∩l3=B,∴l2,l3确定一个平面β.
∵A∈l2,l2 α,∴A∈α.
∵A∈l2,l2 β,∴A∈β.
∵不共线的三个点A,B,C既在平面α内,又在平面β内,
∴平面α和平面β重合,即直线l1,l2,l3在同一平面内.
同理可证,B∈α,B∈β,C∈α,C∈β.
初步应用
例3 已知△ABC在平面α外,它的三边所在的直线分别交平面α于P,Q,R(如图).求证:P,Q,R三点共线.
P
α
Q
R
A
B
C
解析:法一 ∵AB∩α=P,∴P∈AB,P∈平面α.
又AB 平面ABC,∴P∈平面ABC.
∴由公理3可知,点P在平面ABC与平面α的交线上.
同理可证Q,R也在平面ABC与平面α的交线上.
∴P,Q,R三点共线.
初步应用
例3 已知△ABC在平面α外,它的三边所在的直线分别交平面α于P,Q,R(如图).求证:P,Q,R三点共线.
P
α
Q
R
A
B
C
解析:法二 ∵AP∩AR=A,∴直线AP与直线AR确定平面APR.
又∵AB∩α=P,AC∩α=R,
∵B∈平面APR,C∈平面APR,
∴BC 平面APR.又∵Q∈直线BC,
∴Q∈PR,∴P,Q,R三点共线.
∴平面APR∩平面α=PR.
∴Q∈平面APR.又Q∈α,
课堂练习
练习:教科书第210页练习1,2,3.
归纳小结
(1)证明多点共线主要采用什么方法?
(2)证明三线共点问题的主要方法是什么?
问题9 本节课我们学习了直观图的画法,请你通过下列问题,归纳所学知识.
(1)一是首先确定两个平面,然后证明这些点是这两个平面的公共点,再根据基本事实3,这些点都
在这两个平面的交线上;
二是选择其中两点确定一条直线,然后再证明其他的点都在这条直线上.
是这两个平面的交线.
(2)主要方法是先确定两条直线交于一点,再证明该点是这两条直线所在平面的公共点,第三条直线
作业布置
作业:教科书第214页A组第2,3,4,5,6题.
1
目标检测
C
设平面α与平面β交于直线l,A∈α,B∈α,且直线AB∩l=C,则直线AB∩β=________.
解析:∵α∩β=l,AB∩l=C,
∴C∈β,C∈AB,
∴AB∩β=C.
2
目标检测
D
如果两个平面有一个公共点,那么这两个平面( )
A.没有其他公共点
B.仅有这一个公共点
C.仅有两个公共点
D.有无数个公共点
解析:根据基本事实3可知,若两个平面有一个公共点,
则这两个平面有且只有一条经过该点的公共直线.
故选D.
3
目标检测
②
下列命题:
①若直线a与平面α有公共点,则称a α;
③三条平行直线共面;
④若点A,B,C,D共面,点A,B,C,E共面,则点A,B,C,D,E共面.
其中正确的命题是________.(填序号)
②若M∈α,M∈β,α∩β=l,则M∈l;
解析:①错误,若直线a与平面α有公共点,则a与α相交或a α;
②正确,由基本事实3知该命题正确;
③错误,三条平行直线不一定共面,例如三棱柱的三条侧棱;
④错误,如图,两个相交平面有三个公共点A,B,C,但A,B,C,D,E不共面.
4
目标检测
求证:P,Q,R三点共线.
如图所示,AB∩α=P,CD∩α=P,A,D与B,C分别在平面α的两侧,AC∩α=Q,BD∩α=R.
证明:∵AB∩α=P,CD∩α=P,∴AB∩CD=P,
∴AB,CD可确定一个平面,设为β.
∴A∈β,C∈β,B∈β,D∈β,
∵AB∩α=P,AC∩α=Q,BD∩α=R,
∴AC β,BD β,平面α,β相交.
∴P,Q,R三点是平面α与平面β的公共点,
∴P,Q,R都在α与β的交线上,故P,Q,R三点共线.
∵A∈AB,C∈CD,B∈AB,D∈CD,
6.3 空间点、直线、平面之间的位置关系
第1课时
导入新课
问题1 观察下图中的长方体,它有几个顶点?几条棱?几个面?
A
B
C
D
C1
D1
B1
A1
长方体有8个顶点、12条棱、6个面
追问1 长方体的12条棱中,棱与棱有几种位置关系?
棱与棱的位置关系有:相交,平行,既不平行也不相交.
导入新课
追问2 长方体的12条棱和6个面之间有哪些关系?
棱在平面内,棱所在直线与平面平行,棱所在直线与平面相交.
追问3 6个面之间有哪几种位置关系?
6个面之间的位置关系有平行和相交.
新知探究
问题2 平面α是由点组成的,直线l也是由点组成的,从集合的观点看,点P与直线l有何关系?点P与平面α有何关系?直线l与平面α呢?
点P与直线l的关系:P在l上或P不在l上;
直线 l 与平面α的关系:l在α内、l与α平行、l与α相交.
点P与平面α的关系:P在α内或P不在α内;
P∈l
P∈α
P l
P α
l α
l α
l α
新知探究
直线l1与直线l2有相交和不相交两种,相交记作l1∩l2=P,不相交记为l1∩l2= .
直线与平面的位置关系有三种:直线在平面内、直线与平面相交、直线与平面平行.
追问2 直线与平面有几种位置关系?
追问1 直线与直线有几种位置关系?
l在α内
l与α相交
l与α平行
l1∩l2=
l1∩l2=P
新知探究
直线l在平面α内,记作 l α;
直线 l 与α平行,记作 l∥α l∩α= .
追问3 直线 l 在平面α内如何表示?直线l与α平行呢?
新知探究
追问4 平面与平面有几种位置关系?如何表示?
平面与平面平行和平面与平面相交两种.
平面α与平面β平行,记作α∥β,它等价于α∩β= .
平面α与平面β相交于直线l,记作α∩β=l.
新知探究
因为不在同一直线上的三点可以确定一个平面.
故三脚架可以牢固地支撑照相机或测量用的平板仪.
不一定.只有经过空间不共线的三点才能确定一个平面.
问题3 生活中常见到这样的现象:三脚架可以牢固地支撑照相机或测量用的平板仪等,请问这是为什么?
追问 经过空间任意三点能确定一个平面吗?
新知探究
问题4 若把直尺边缘上的任意两点放在桌面上,直尺的边缘上的其余点和桌面有何关系?
直尺边缘上的其余点都在桌面上.
追问 如何判断直线在平面内?
因为两点确定一条直线,
所以只要直线上的两点在一个平面内,这条直线就在这个平面内.
新知探究
问题5 下列说法是否正确?并说明理由.
这三个结论都正确,由基本事实1,2可以推证.
(1)一条直线和直线外一点确定一个平面.
(2)两条相交直线确定一个平面.
(3)两条平行直线确定一个平面.
新知探究
问题6 观察正方体ABCD-A1B1C1D1(如图所示),平面ABCD与平面BCC1B1有且只有两个公共点B,C吗?
不是.平面ABCD∩平面BCC1B1=BC.
不可能.因为平面是无限延展的,所以两平面的交线是一条直线.
A
B
C
D
C1
D1
B1
A1
追问 两个平面的交线可能是一条线段吗?
新知探究
问题7 你能叙述基本事实1,2,3吗?
基本事实1:过不在一条直线上的三个点,有且只有一个平面.
基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有过该点的公共直线.
基本事实2:如果一条直线上的两点在一个平面内,那么这条直线在这个平面内
(即直线在平面内).
α
A
B
C
●
●
●
A
B
l
α
●
●
α
β
P
l
新知探究
问题8 由基本事实3,你能得出判断直线共面的什么条件?
基本事实2的推论
推论1:一条直线和直线外一点确定一个平面;
推论2:两条相交直线确定一个平面;
推论3:两条平行直线确定一个平面.
α
B
C
A
●
a
●
●
A
α
B
C
●
●
●
α
C
A
B
●
●
●
a
b
初步应用
例1 用符号表示下列语句,并画出图形.
(1)平面α与β相交于直线l,直线a与α,β分别相交于点A,B;
(2)点A,B在平面α内,直线a与平面α交于点C,点C不在直线AB上.
解析:
(2)用符号表示:A∈α,B∈α,a∩α=C,C AB,如图2.
(1)用符号表示:α∩β=l,a∩α=A,a∩β=B,如图1.
图1
图2
例2 证明:两两相交且不共点的三条直线在同一平面内.
初步应用
已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.
求证:直线l1,l2,l3在同一平面内.
解析:法一 ∵l1∩l2=A,∴l1和l2确定一个平面α.
∵l2∩l3=B,∴B∈l2又l2 α,∴B∈α.
同理可证C∈α,又B∈l3,C∈l3,∴l3 α.
∴直线l1,l2,l3在同一平面内.
例2 证明:两两相交且不共点的三条直线在同一平面内.
初步应用
解析:法二 ∵l1∩l2=A,∴l1,l2确定一个平面α.
∵l2∩l3=B,∴l2,l3确定一个平面β.
∵A∈l2,l2 α,∴A∈α.
∵A∈l2,l2 β,∴A∈β.
∵不共线的三个点A,B,C既在平面α内,又在平面β内,
∴平面α和平面β重合,即直线l1,l2,l3在同一平面内.
同理可证,B∈α,B∈β,C∈α,C∈β.
初步应用
例3 已知△ABC在平面α外,它的三边所在的直线分别交平面α于P,Q,R(如图).求证:P,Q,R三点共线.
P
α
Q
R
A
B
C
解析:法一 ∵AB∩α=P,∴P∈AB,P∈平面α.
又AB 平面ABC,∴P∈平面ABC.
∴由公理3可知,点P在平面ABC与平面α的交线上.
同理可证Q,R也在平面ABC与平面α的交线上.
∴P,Q,R三点共线.
初步应用
例3 已知△ABC在平面α外,它的三边所在的直线分别交平面α于P,Q,R(如图).求证:P,Q,R三点共线.
P
α
Q
R
A
B
C
解析:法二 ∵AP∩AR=A,∴直线AP与直线AR确定平面APR.
又∵AB∩α=P,AC∩α=R,
∵B∈平面APR,C∈平面APR,
∴BC 平面APR.又∵Q∈直线BC,
∴Q∈PR,∴P,Q,R三点共线.
∴平面APR∩平面α=PR.
∴Q∈平面APR.又Q∈α,
课堂练习
练习:教科书第210页练习1,2,3.
归纳小结
(1)证明多点共线主要采用什么方法?
(2)证明三线共点问题的主要方法是什么?
问题9 本节课我们学习了直观图的画法,请你通过下列问题,归纳所学知识.
(1)一是首先确定两个平面,然后证明这些点是这两个平面的公共点,再根据基本事实3,这些点都
在这两个平面的交线上;
二是选择其中两点确定一条直线,然后再证明其他的点都在这条直线上.
是这两个平面的交线.
(2)主要方法是先确定两条直线交于一点,再证明该点是这两条直线所在平面的公共点,第三条直线
作业布置
作业:教科书第214页A组第2,3,4,5,6题.
1
目标检测
C
设平面α与平面β交于直线l,A∈α,B∈α,且直线AB∩l=C,则直线AB∩β=________.
解析:∵α∩β=l,AB∩l=C,
∴C∈β,C∈AB,
∴AB∩β=C.
2
目标检测
D
如果两个平面有一个公共点,那么这两个平面( )
A.没有其他公共点
B.仅有这一个公共点
C.仅有两个公共点
D.有无数个公共点
解析:根据基本事实3可知,若两个平面有一个公共点,
则这两个平面有且只有一条经过该点的公共直线.
故选D.
3
目标检测
②
下列命题:
①若直线a与平面α有公共点,则称a α;
③三条平行直线共面;
④若点A,B,C,D共面,点A,B,C,E共面,则点A,B,C,D,E共面.
其中正确的命题是________.(填序号)
②若M∈α,M∈β,α∩β=l,则M∈l;
解析:①错误,若直线a与平面α有公共点,则a与α相交或a α;
②正确,由基本事实3知该命题正确;
③错误,三条平行直线不一定共面,例如三棱柱的三条侧棱;
④错误,如图,两个相交平面有三个公共点A,B,C,但A,B,C,D,E不共面.
4
目标检测
求证:P,Q,R三点共线.
如图所示,AB∩α=P,CD∩α=P,A,D与B,C分别在平面α的两侧,AC∩α=Q,BD∩α=R.
证明:∵AB∩α=P,CD∩α=P,∴AB∩CD=P,
∴AB,CD可确定一个平面,设为β.
∴A∈β,C∈β,B∈β,D∈β,
∵AB∩α=P,AC∩α=Q,BD∩α=R,
∴AC β,BD β,平面α,β相交.
∴P,Q,R三点是平面α与平面β的公共点,
∴P,Q,R都在α与β的交线上,故P,Q,R三点共线.
∵A∈AB,C∈CD,B∈AB,D∈CD,
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
