四川省宜宾市部分中学2022-2023学年高三下学期开学考试数学(文)试题(含答案)
文档属性
| 名称 | 四川省宜宾市部分中学2022-2023学年高三下学期开学考试数学(文)试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 561.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 19:37:08 | ||
图片预览



文档简介
宜宾市部分中学2022-2023学年高三下学期开学考试
数 学(文史类)
注意事项:
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号. 回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3. 本试卷满分150分,考试时间120分钟. 考试结束后,请将答题卡交回。
一.选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设复数(其中为虚数单位),则=
A. B.3 C.5 D.
2.已知集合,,则中元素的个数为
A.2 B.3 C.4 D.6
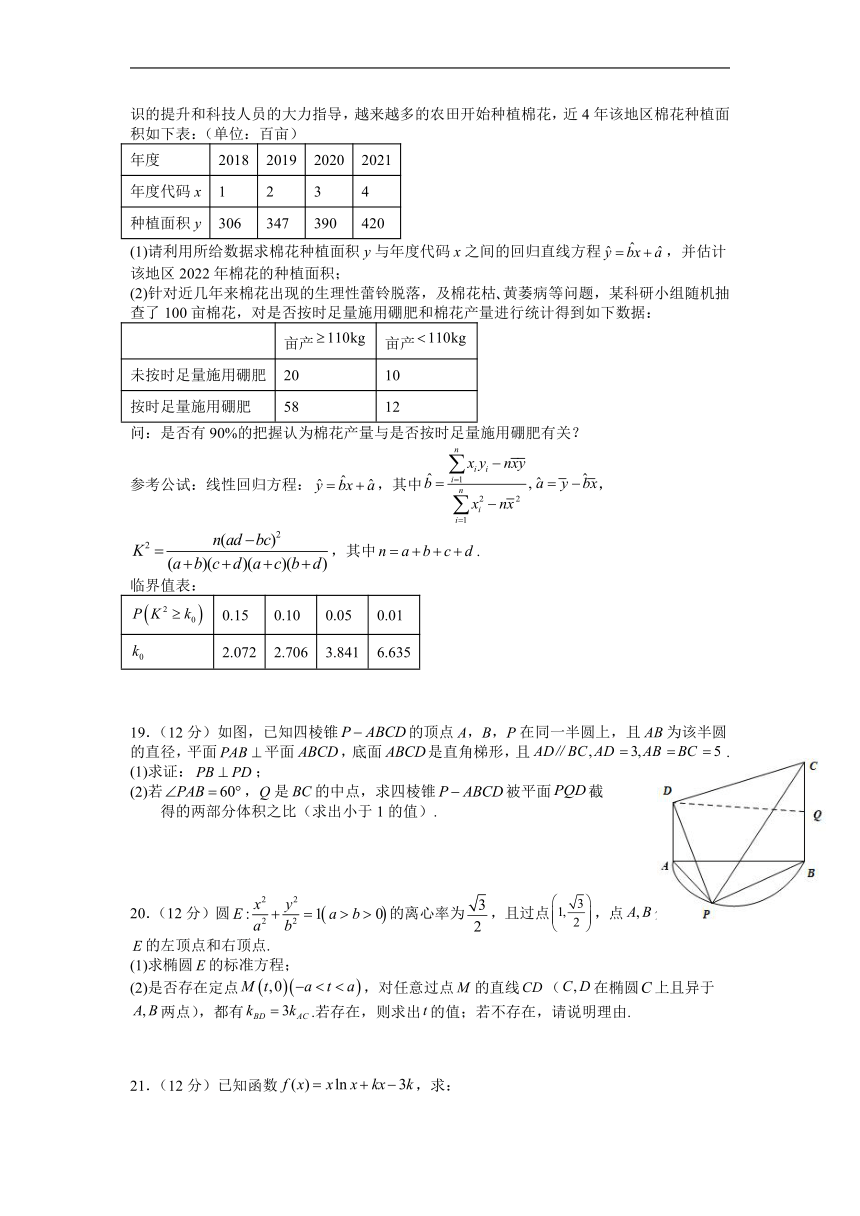
3.函数在上的大致图象为
A. B.
C. D.
4.设一组样本数据x1,x2,…,xn的方差为0.01,则数据10x1,10x2,…,10xn的方差为
A.0.01 B.0.1 C.1 D.10
5.将函数的图象向左平移个单位长度后,所得图象对应的函数为
A. B. C. D.
6.若x,y∈R,,则的最小值是
A.4 B.5 C.7 D.11
7.已知,则
A. B. C. D.
8.医学上用基于SEIR流行病传播模型测算基本传染数(也叫基本再生数)来衡量传染性的强弱,基本传染数可表示为.计算基本传染数需要确定的参数有:(1)参数:,即需要知道第一例病例发生的时间(确定起点以便计算t),以及之后某一时刻的累计病例数,时间t的单位为天数;(2)参数和ρ:只要确定了潜伏期TE和传染期TI,和ρ就都确定了.已知2022年2月15日某地发现首例A型传染性病例,到2022年3月28日累计A型传染性病例数达到425例.取,,根据上面的公式计算这41天A型传染性基本传染数约为(注:参考数据:)
A.2.63 B.2.78 C.2.82 D.3.04
9.设函数,则下列函数中为奇函数的是
A. B. C. D.
10.已知为抛物线上一点,点到的焦点的距离为7,到轴的距离为5,则
A.3 B.4 C.5 D.6
11.已知是以为斜边的直角三角形,为平面外一点,且平面平面,,,,则三棱锥外接球的体积为
A. B. C. D.
12.若,其中,则
A. B. C. D.
二、填空题:本大题共4个小题,每小题5分,共20分.
13.在半径为2的圆上有,两点,且,在该圆上任取一点,则使得为锐角三角形的概率为________.
14.设,是两条不同的直线,,是两个不同的平面,有下列四个命题:
①若,,则; ②若,,,则;
③若,,,,则; ④若,,,则.
其中正确命题的序号为___________.
15.双曲线的左焦点到直线的距离为_______.
16.对于函数,若在定义域内存在实数x,满足,则称为“局部奇函数”.若为定义域R上的“局部奇函数”,则实数m的取值范围为________________
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须答.第22、23题为选考题,考生根据要求作答.
(一)必做题:共60分.
17.(12分)已知数列满足,.
(1)证明:数列是等差数列,并求数列的通项公式;
(2)记,求的前n项和
18.(12分)棉花是我国主要经济作物 纺织工业原料 重要战略物资.量化我国棉花生产碳足迹,解析其时空变化规律,阐明其主要构成因素与影响要素,对于“碳达峰,碳中和”愿景下我国棉花绿色可持续生产具有重要意义.某地因地制宜发展特色棉花种植,随着人们种植意识的提升和科技人员的大力指导,越来越多的农田开始种植棉花,近4年该地区棉花种植面积如下表:(单位:百亩)
年度 2018 2019 2020 2021
年度代码x 1 2 3 4
种植面积y 306 347 390 420
(1)请利用所给数据求棉花种植面积y与年度代码x之间的回归直线方程,并估计该地区2022年棉花的种植面积;
(2)针对近几年来棉花出现的生理性蕾铃脱落,及棉花枯 黄萎病等问题,某科研小组随机抽查了100亩棉花,对是否按时足量施用硼肥和棉花产量进行统计得到如下数据:
亩产 亩产
未按时足量施用硼肥 20 10
按时足量施用硼肥 58 12
问:是否有90%的把握认为棉花产量与是否按时足量施用硼肥有关?
参考公试:线性回归方程:,其中,,其中.
临界值表:
0.15 0.10 0.05 0.01
2.072 2.706 3.841 6.635
19.(12分)如图,已知四棱锥的顶点A,B,P在同一半圆上,且为该半圆的直径,平面平面,底面是直角梯形,且.
(1)求证:;
(2)若,Q是的中点,求四棱锥被平面截
得的两部分体积之比(求出小于1的值).
20.(12分)圆的离心率为,且过点,点分别为椭圆的左顶点和右顶点.
(1)求椭圆的标准方程;
(2)是否存在定点,对任意过点的直线(在椭圆上且异于两点),都有.若存在,则求出的值;若不存在,请说明理由.
21.(12分)已知函数,求:
(1)当时,求曲线在点处的切线方程;
(2)当时,总有,求整数的最小值.
(二)选做题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题记分.
22.(10分)选修4-4:坐标系与参数方程
已知曲线的参数方程为(为参数),曲线的极坐标方程为.
(1)将曲线的参数方程化为普通方程,将曲线的极坐标方程化为直角坐标方程;
(2)曲线,是否相交?若相交,请求出公共弦的长,若不相交,请说明理由.
23.(10分)选修4-5:不等式选讲
已知函数,若不等式的解集为.
(1)求的值;
(2)若存在,使得不等式成立,求的取值范围.
宜宾市部分中学2022-2023学年高三下学期开学考试
数 学(文史类)参考答案:
1.A 2.C 3.C 4.C 5.B 6.B 7.A 8.D 9.B 10.B 11.D 12.D
13. 14.② 15.2 16.
17.(1)当时,,得,
当时,有,,
相除得
整理为:,
即,
∴为等差数列,公差,首项为;
所以,整理为:.
(2),
18.(1)根据题意得到,
因为,
所以,
所以棉花种植面积y与年度代码x之间的回归直线方程,
当时,,
所以估计该地区2022年棉花的种植面积为462百亩.
(2)结合已知数据得到列联表如下表所示:
亩产 亩产 合计
未按时足量施用硼肥 20 10 30
按时足量施用硼肥 58 12 70
合计 78 22 100
,
所以有90%的把握认为棉花产量与是否按时足量施用硼肥有关.
19.(1)因为平面平面,平面平面,底面是直角梯形,所以,所以平面,又平面,所以;
因为A,B,P在同一半圆上,且为该半圆的直径,所以,
因为,所以平面,又因为平面,所以;
(2)
如图,连接,则四棱锥被平面切割为和两部分,因为两棱锥高相同,故,
因为Q是的中点,,所以,,,
所以,.
20.(1)由题意得:,解得:,
椭圆的标准方程为;
(2)由(1)知:,;
①当直线斜率不存在时,由得:或,
若,,
则,,,解得:;
若,,同理可求得:;
②当直线斜率存在时,设,,则;
设直线,
由得:,
,解得:,,
又,同理可得:,,
,整理可得:,
当时,恒成立;
综上所述:存在满足题意的点,使得恒成立,此时.
21.(1)当时,
在点处的切线方程为即
(2)由题意,,即,即,
又,恒成立.令,
令,则恒成立.在上递减,
,
使,即,则,
当时,,当时,
因为,且,,即整数k的最小值为-3
22.(1)由消去参数得:,所以曲线的普通方程为,
由得:,将代入得:
,即,
所以曲线的直角坐标方程为;
(2)由(1)知曲线是以为圆心,为半径的圆,曲线是以为圆心,为半径的圆,
于是得,即圆与圆相交,
设公共弦长为,因两圆半径相等,从而得公共弦垂直平分线段,
于是得,解得,所以公共弦长为.
23.解:(1)∵,∴,即,解得,
又∵不等式的解集为,∴.
(2)依题意,,故不等式可化为,
要使不等式存在解,即存在解,即存在解,
令,∴的最小值为,依题意得,
∴.
数 学(文史类)
注意事项:
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号. 回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3. 本试卷满分150分,考试时间120分钟. 考试结束后,请将答题卡交回。
一.选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设复数(其中为虚数单位),则=
A. B.3 C.5 D.
2.已知集合,,则中元素的个数为
A.2 B.3 C.4 D.6
3.函数在上的大致图象为
A. B.
C. D.
4.设一组样本数据x1,x2,…,xn的方差为0.01,则数据10x1,10x2,…,10xn的方差为
A.0.01 B.0.1 C.1 D.10
5.将函数的图象向左平移个单位长度后,所得图象对应的函数为
A. B. C. D.
6.若x,y∈R,,则的最小值是
A.4 B.5 C.7 D.11
7.已知,则
A. B. C. D.
8.医学上用基于SEIR流行病传播模型测算基本传染数(也叫基本再生数)来衡量传染性的强弱,基本传染数可表示为.计算基本传染数需要确定的参数有:(1)参数:,即需要知道第一例病例发生的时间(确定起点以便计算t),以及之后某一时刻的累计病例数,时间t的单位为天数;(2)参数和ρ:只要确定了潜伏期TE和传染期TI,和ρ就都确定了.已知2022年2月15日某地发现首例A型传染性病例,到2022年3月28日累计A型传染性病例数达到425例.取,,根据上面的公式计算这41天A型传染性基本传染数约为(注:参考数据:)
A.2.63 B.2.78 C.2.82 D.3.04
9.设函数,则下列函数中为奇函数的是
A. B. C. D.
10.已知为抛物线上一点,点到的焦点的距离为7,到轴的距离为5,则
A.3 B.4 C.5 D.6
11.已知是以为斜边的直角三角形,为平面外一点,且平面平面,,,,则三棱锥外接球的体积为
A. B. C. D.
12.若,其中,则
A. B. C. D.
二、填空题:本大题共4个小题,每小题5分,共20分.
13.在半径为2的圆上有,两点,且,在该圆上任取一点,则使得为锐角三角形的概率为________.
14.设,是两条不同的直线,,是两个不同的平面,有下列四个命题:
①若,,则; ②若,,,则;
③若,,,,则; ④若,,,则.
其中正确命题的序号为___________.
15.双曲线的左焦点到直线的距离为_______.
16.对于函数,若在定义域内存在实数x,满足,则称为“局部奇函数”.若为定义域R上的“局部奇函数”,则实数m的取值范围为________________
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须答.第22、23题为选考题,考生根据要求作答.
(一)必做题:共60分.
17.(12分)已知数列满足,.
(1)证明:数列是等差数列,并求数列的通项公式;
(2)记,求的前n项和
18.(12分)棉花是我国主要经济作物 纺织工业原料 重要战略物资.量化我国棉花生产碳足迹,解析其时空变化规律,阐明其主要构成因素与影响要素,对于“碳达峰,碳中和”愿景下我国棉花绿色可持续生产具有重要意义.某地因地制宜发展特色棉花种植,随着人们种植意识的提升和科技人员的大力指导,越来越多的农田开始种植棉花,近4年该地区棉花种植面积如下表:(单位:百亩)
年度 2018 2019 2020 2021
年度代码x 1 2 3 4
种植面积y 306 347 390 420
(1)请利用所给数据求棉花种植面积y与年度代码x之间的回归直线方程,并估计该地区2022年棉花的种植面积;
(2)针对近几年来棉花出现的生理性蕾铃脱落,及棉花枯 黄萎病等问题,某科研小组随机抽查了100亩棉花,对是否按时足量施用硼肥和棉花产量进行统计得到如下数据:
亩产 亩产
未按时足量施用硼肥 20 10
按时足量施用硼肥 58 12
问:是否有90%的把握认为棉花产量与是否按时足量施用硼肥有关?
参考公试:线性回归方程:,其中,,其中.
临界值表:
0.15 0.10 0.05 0.01
2.072 2.706 3.841 6.635
19.(12分)如图,已知四棱锥的顶点A,B,P在同一半圆上,且为该半圆的直径,平面平面,底面是直角梯形,且.
(1)求证:;
(2)若,Q是的中点,求四棱锥被平面截
得的两部分体积之比(求出小于1的值).
20.(12分)圆的离心率为,且过点,点分别为椭圆的左顶点和右顶点.
(1)求椭圆的标准方程;
(2)是否存在定点,对任意过点的直线(在椭圆上且异于两点),都有.若存在,则求出的值;若不存在,请说明理由.
21.(12分)已知函数,求:
(1)当时,求曲线在点处的切线方程;
(2)当时,总有,求整数的最小值.
(二)选做题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题记分.
22.(10分)选修4-4:坐标系与参数方程
已知曲线的参数方程为(为参数),曲线的极坐标方程为.
(1)将曲线的参数方程化为普通方程,将曲线的极坐标方程化为直角坐标方程;
(2)曲线,是否相交?若相交,请求出公共弦的长,若不相交,请说明理由.
23.(10分)选修4-5:不等式选讲
已知函数,若不等式的解集为.
(1)求的值;
(2)若存在,使得不等式成立,求的取值范围.
宜宾市部分中学2022-2023学年高三下学期开学考试
数 学(文史类)参考答案:
1.A 2.C 3.C 4.C 5.B 6.B 7.A 8.D 9.B 10.B 11.D 12.D
13. 14.② 15.2 16.
17.(1)当时,,得,
当时,有,,
相除得
整理为:,
即,
∴为等差数列,公差,首项为;
所以,整理为:.
(2),
18.(1)根据题意得到,
因为,
所以,
所以棉花种植面积y与年度代码x之间的回归直线方程,
当时,,
所以估计该地区2022年棉花的种植面积为462百亩.
(2)结合已知数据得到列联表如下表所示:
亩产 亩产 合计
未按时足量施用硼肥 20 10 30
按时足量施用硼肥 58 12 70
合计 78 22 100
,
所以有90%的把握认为棉花产量与是否按时足量施用硼肥有关.
19.(1)因为平面平面,平面平面,底面是直角梯形,所以,所以平面,又平面,所以;
因为A,B,P在同一半圆上,且为该半圆的直径,所以,
因为,所以平面,又因为平面,所以;
(2)
如图,连接,则四棱锥被平面切割为和两部分,因为两棱锥高相同,故,
因为Q是的中点,,所以,,,
所以,.
20.(1)由题意得:,解得:,
椭圆的标准方程为;
(2)由(1)知:,;
①当直线斜率不存在时,由得:或,
若,,
则,,,解得:;
若,,同理可求得:;
②当直线斜率存在时,设,,则;
设直线,
由得:,
,解得:,,
又,同理可得:,,
,整理可得:,
当时,恒成立;
综上所述:存在满足题意的点,使得恒成立,此时.
21.(1)当时,
在点处的切线方程为即
(2)由题意,,即,即,
又,恒成立.令,
令,则恒成立.在上递减,
,
使,即,则,
当时,,当时,
因为,且,,即整数k的最小值为-3
22.(1)由消去参数得:,所以曲线的普通方程为,
由得:,将代入得:
,即,
所以曲线的直角坐标方程为;
(2)由(1)知曲线是以为圆心,为半径的圆,曲线是以为圆心,为半径的圆,
于是得,即圆与圆相交,
设公共弦长为,因两圆半径相等,从而得公共弦垂直平分线段,
于是得,解得,所以公共弦长为.
23.解:(1)∵,∴,即,解得,
又∵不等式的解集为,∴.
(2)依题意,,故不等式可化为,
要使不等式存在解,即存在解,即存在解,
令,∴的最小值为,依题意得,
∴.
同课章节目录
