方程整理与复习(课件)五年级下册数学苏教版(共21张PPT)
文档属性
| 名称 | 方程整理与复习(课件)五年级下册数学苏教版(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 419.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 20:40:46 | ||
图片预览






文档简介
(共21张PPT)
方程整理与复习
数学小讲师
世界人均土地面积大约是2.34公顷,相当于我国人均土地面积的3倍。我国人均土地面积大约是多少公顷?
我国人均土地面积×3 =世界人均土地面积
解:设我国人均土地面积大约是x 公顷。
3x = 2.34
x = 2.34÷3
x = 0.78
答:我国人均土地面积大约是0.78公顷。
题中的数量间有什么关系?
本节课你想从哪几个方面进行复习?
提出问题
1.本学期我们学习了整数和分数的哪些知识?
2.列方程解决实际问题时要注意什么?
3.你对解决问题的策略有哪些新的认识?
小组交流思维导图
回顾与整理
数
的
世
界
方程
等
式
的
性
质
等式两边同时加上或减去同一个数,所得结果仍然是等式,这就是等式的性质。
等式两边同时乘或除以同一个不是0的数,所得结果仍然是等式,这就是等式的性质。
含有未知数的等式是方程。
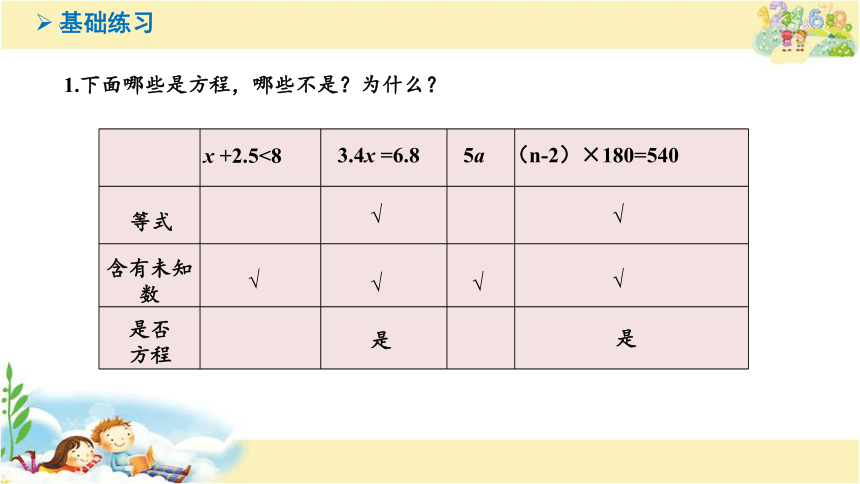
1.下面哪些是方程,哪些不是?为什么?
(n-2)×180=540
5a
x +2.5<8
3.4x =6.8
思考:判断是不是方程的依据是什么?
1.是等式
2.含有未知数
基础练习
等式
含有未知数
(n-2)×180=540
x +2.5<8
3.4x =6.8
5a
√
√
√
√
√
√
是否方程
是
是
基础练习
1.下面哪些是方程,哪些不是?为什么?
基础练习
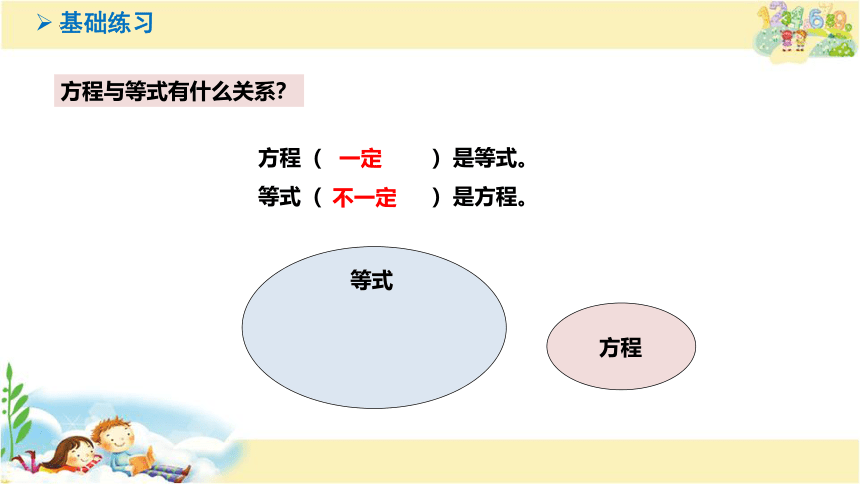
方程与等式有什么关系?
等式
方程
方程( )是等式。
等式( )是方程。
一定
不一定
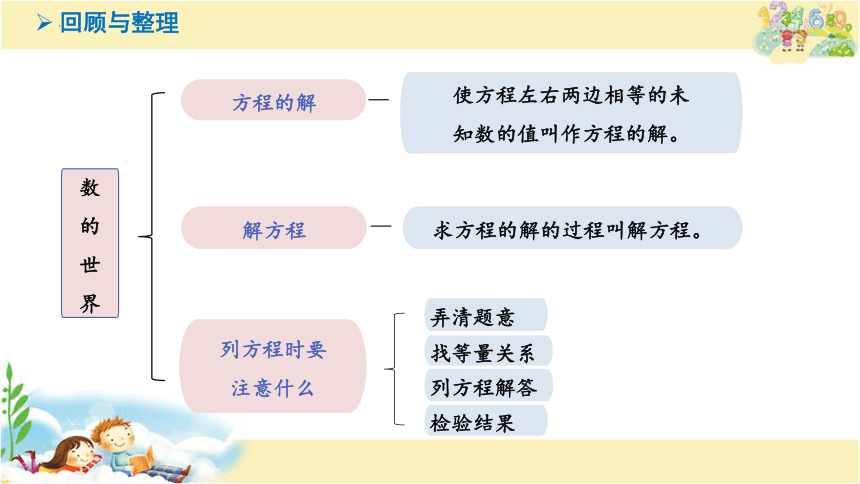
方程的解
列方程时要
注意什么
使方程左右两边相等的未
知数的值叫作方程的解。
找等量关系
回顾与整理
数
的
世
界
解方程
求方程的解的过程叫解方程。
弄清题意
列方程解答
检验结果
x÷12 = 180
解: x÷12 ×12 = 180×12
x = 2160
24x+38x = 310
解: 62x = 310
x = 5
2.5x-0.5×8 = 6
解: 2.5x = 6+4
x = 4
62x÷62 = 310÷62
x = 10÷2.5
解方程时要注意什么?
2.解方程
要注意正确运用等式的性质,并检验。
基础练习
x = 310÷62
x = 180×12
三角形面积550cm2
找出数量关系
22 x ÷2 = 550
22x = 550×2
x = 50
22x = 1100
3.求x的值
底×高÷ 2 =三角形的面积
基础练习
解:
x = 3
x +1.5 = 4.5
(x +1.5)×2 = 9
x +1.5 = 9÷2
长方形周长9m
(长+宽)×2 =长方形的周长
基础练习
3.求x的值
找出数量关系
解:
x = 3
2x = 6
2x +1.5×2 = 9
2x = 9-3
长×2 +宽×2 = 长方形的周长
解:
4.少先队员采集植物标本和昆虫标本共60件,植物标本的件数是昆虫标本的1.5倍,两种标本各有多少件?
小提示:
1.列方程依据的是哪个等量关系?
2.题中是怎样设未知数的?
昆虫标本件数 + 植物标本件数 = 总件数
解:设昆虫标本有x件,则植物标本有1.5x件。
x +1.5x = 60
2.5x = 60
x = 24
1.5x=1.5×24=36
答:昆虫标本有24件,植物标本有36件。
巩固提升
检验:24+36=60(件)
36÷24=1.5
5.一只大熊猫满月时的体重大约是刚出生时的7.8倍,比刚出生时增加了578克,这只大熊猫刚出生时体重是多少克?满月时呢?
大熊猫满月体重-出生体重 = 比出生时增加的体重
解:设这只大熊猫刚出生时体重是x克,则满月时是7.8x克。
7.8x-x = 578
6.8x = 578
x = 85
7.8x=7.8×85=663
答:这只大熊猫刚出生时体重是85克,满月时是663克。
题中的数量间有什么关系?
巩固提升
检验:663-85=578(件)
663÷85=7.8
巩固提升
4.少先队员采集植物标本和昆虫标本共60件,植物标本的件数是昆虫标本的1.5倍,两种标本各有多少件?
昆虫标本件数 + 植物标本件数 = 总件数
解:设昆虫标本有x件,则植物标本有1.5x件。
x +1.5x = 60
2.5x = 60
x = 24
1.5x=1.5×24=36
答:昆虫标本有24件,植物标本有36件。
5.一只大熊猫满月时的体重大约是刚出生时的7.8倍,比刚出生时增加了578克,这只大熊猫刚出生时体重是多少克?满月时呢?
大熊猫满月体重-出生体重 = 比出生时增加的体重
解:设这只大熊猫刚出生时体重是x克,则满月时是7.8x克。
7.8x-x = 578
6.8x = 578
x = 85
7.8x=7.8×85=663
答:这只大熊猫刚出生时体重是85克,满月时是663克。
比较:这两题方程表示的意思有什么不同?
6.南京长江大桥南、北两个桥头堡大约相距1573米。红红、军军分别从南、北桥头堡同时出发,相向而行,经过13分钟相遇。军军的速度是63米/分,红红的速度是多少?
速度和×相遇时间=总路程
红红所行路程+军军所行路程=总路程
巩固提升
题中的数量间有什么关系?
解:设红红的速度是x米/分。
速度和×相遇时间=总路程
(63+x)× 13 = 1573
63+x = 121
x = 58
63+x = 1573÷13
答:红红的速度是58米/分。
巩固提升
6.南京长江大桥南、北两个桥头堡大约相距1573米。红红、军军分别从南、北桥头堡同时出发,相向而行,经过13分钟相遇。军军的速度是63米/分,红红的速度是多少?
解:设红红的速度是x米/分。
红红所行路程+军军所行路程=总路程
13 x + 63 × 13 = 1573
13 + 819 = 1573
13x = 754
x = 58
答:红红的速度是58米/分。
巩固提升
6.南京长江大桥南、北两个桥头堡大约相距1573米。红红、军军分别从南、北桥头堡同时出发,相向而行,经过13分钟相遇。军军的速度是63米/分,红红的速度是多少?
拓展延伸
兄弟三人的年龄是三个连续的偶数。他们的年龄和是180岁,他们三人的年龄分别是多少岁?
老三的年龄+老二的年龄+老大的年龄=年龄和
小提示:
1.什么样的数是偶数,连续是什么意思?
2你能找出数量关系式吗?
拓展延伸
答:老大的年龄是62岁,老二的年龄是60岁,
老三的年龄是58岁。
兄弟三人的年龄是三个连续的偶数。他们的年龄和是180岁,他们三人的年龄分别是多少岁?
解:设老二的年龄是x岁,则老大的年龄是(x+2)岁,
老三的年龄是(x-2)岁。
(x-2)+ x +(x+2) = 180
3x = 180
x = 60
x+2=60+2=62
x-2=60-2=58
拓展延伸
兄弟三人的年龄是三个连续的偶数。他们的年龄和是180岁,他们三人的年龄分别是多少岁?
老大:60 + 2 = 62(岁)
老二:180÷3=60(岁)
老三:60-2 = 58(岁)
答:老大的年龄是62岁,老二的年龄是60岁,
老三的年龄是58岁。
回顾反思
通过这节课的学习,你有什么收获
方程整理与复习
数学小讲师
世界人均土地面积大约是2.34公顷,相当于我国人均土地面积的3倍。我国人均土地面积大约是多少公顷?
我国人均土地面积×3 =世界人均土地面积
解:设我国人均土地面积大约是x 公顷。
3x = 2.34
x = 2.34÷3
x = 0.78
答:我国人均土地面积大约是0.78公顷。
题中的数量间有什么关系?
本节课你想从哪几个方面进行复习?
提出问题
1.本学期我们学习了整数和分数的哪些知识?
2.列方程解决实际问题时要注意什么?
3.你对解决问题的策略有哪些新的认识?
小组交流思维导图
回顾与整理
数
的
世
界
方程
等
式
的
性
质
等式两边同时加上或减去同一个数,所得结果仍然是等式,这就是等式的性质。
等式两边同时乘或除以同一个不是0的数,所得结果仍然是等式,这就是等式的性质。
含有未知数的等式是方程。
1.下面哪些是方程,哪些不是?为什么?
(n-2)×180=540
5a
x +2.5<8
3.4x =6.8
思考:判断是不是方程的依据是什么?
1.是等式
2.含有未知数
基础练习
等式
含有未知数
(n-2)×180=540
x +2.5<8
3.4x =6.8
5a
√
√
√
√
√
√
是否方程
是
是
基础练习
1.下面哪些是方程,哪些不是?为什么?
基础练习
方程与等式有什么关系?
等式
方程
方程( )是等式。
等式( )是方程。
一定
不一定
方程的解
列方程时要
注意什么
使方程左右两边相等的未
知数的值叫作方程的解。
找等量关系
回顾与整理
数
的
世
界
解方程
求方程的解的过程叫解方程。
弄清题意
列方程解答
检验结果
x÷12 = 180
解: x÷12 ×12 = 180×12
x = 2160
24x+38x = 310
解: 62x = 310
x = 5
2.5x-0.5×8 = 6
解: 2.5x = 6+4
x = 4
62x÷62 = 310÷62
x = 10÷2.5
解方程时要注意什么?
2.解方程
要注意正确运用等式的性质,并检验。
基础练习
x = 310÷62
x = 180×12
三角形面积550cm2
找出数量关系
22 x ÷2 = 550
22x = 550×2
x = 50
22x = 1100
3.求x的值
底×高÷ 2 =三角形的面积
基础练习
解:
x = 3
x +1.5 = 4.5
(x +1.5)×2 = 9
x +1.5 = 9÷2
长方形周长9m
(长+宽)×2 =长方形的周长
基础练习
3.求x的值
找出数量关系
解:
x = 3
2x = 6
2x +1.5×2 = 9
2x = 9-3
长×2 +宽×2 = 长方形的周长
解:
4.少先队员采集植物标本和昆虫标本共60件,植物标本的件数是昆虫标本的1.5倍,两种标本各有多少件?
小提示:
1.列方程依据的是哪个等量关系?
2.题中是怎样设未知数的?
昆虫标本件数 + 植物标本件数 = 总件数
解:设昆虫标本有x件,则植物标本有1.5x件。
x +1.5x = 60
2.5x = 60
x = 24
1.5x=1.5×24=36
答:昆虫标本有24件,植物标本有36件。
巩固提升
检验:24+36=60(件)
36÷24=1.5
5.一只大熊猫满月时的体重大约是刚出生时的7.8倍,比刚出生时增加了578克,这只大熊猫刚出生时体重是多少克?满月时呢?
大熊猫满月体重-出生体重 = 比出生时增加的体重
解:设这只大熊猫刚出生时体重是x克,则满月时是7.8x克。
7.8x-x = 578
6.8x = 578
x = 85
7.8x=7.8×85=663
答:这只大熊猫刚出生时体重是85克,满月时是663克。
题中的数量间有什么关系?
巩固提升
检验:663-85=578(件)
663÷85=7.8
巩固提升
4.少先队员采集植物标本和昆虫标本共60件,植物标本的件数是昆虫标本的1.5倍,两种标本各有多少件?
昆虫标本件数 + 植物标本件数 = 总件数
解:设昆虫标本有x件,则植物标本有1.5x件。
x +1.5x = 60
2.5x = 60
x = 24
1.5x=1.5×24=36
答:昆虫标本有24件,植物标本有36件。
5.一只大熊猫满月时的体重大约是刚出生时的7.8倍,比刚出生时增加了578克,这只大熊猫刚出生时体重是多少克?满月时呢?
大熊猫满月体重-出生体重 = 比出生时增加的体重
解:设这只大熊猫刚出生时体重是x克,则满月时是7.8x克。
7.8x-x = 578
6.8x = 578
x = 85
7.8x=7.8×85=663
答:这只大熊猫刚出生时体重是85克,满月时是663克。
比较:这两题方程表示的意思有什么不同?
6.南京长江大桥南、北两个桥头堡大约相距1573米。红红、军军分别从南、北桥头堡同时出发,相向而行,经过13分钟相遇。军军的速度是63米/分,红红的速度是多少?
速度和×相遇时间=总路程
红红所行路程+军军所行路程=总路程
巩固提升
题中的数量间有什么关系?
解:设红红的速度是x米/分。
速度和×相遇时间=总路程
(63+x)× 13 = 1573
63+x = 121
x = 58
63+x = 1573÷13
答:红红的速度是58米/分。
巩固提升
6.南京长江大桥南、北两个桥头堡大约相距1573米。红红、军军分别从南、北桥头堡同时出发,相向而行,经过13分钟相遇。军军的速度是63米/分,红红的速度是多少?
解:设红红的速度是x米/分。
红红所行路程+军军所行路程=总路程
13 x + 63 × 13 = 1573
13 + 819 = 1573
13x = 754
x = 58
答:红红的速度是58米/分。
巩固提升
6.南京长江大桥南、北两个桥头堡大约相距1573米。红红、军军分别从南、北桥头堡同时出发,相向而行,经过13分钟相遇。军军的速度是63米/分,红红的速度是多少?
拓展延伸
兄弟三人的年龄是三个连续的偶数。他们的年龄和是180岁,他们三人的年龄分别是多少岁?
老三的年龄+老二的年龄+老大的年龄=年龄和
小提示:
1.什么样的数是偶数,连续是什么意思?
2你能找出数量关系式吗?
拓展延伸
答:老大的年龄是62岁,老二的年龄是60岁,
老三的年龄是58岁。
兄弟三人的年龄是三个连续的偶数。他们的年龄和是180岁,他们三人的年龄分别是多少岁?
解:设老二的年龄是x岁,则老大的年龄是(x+2)岁,
老三的年龄是(x-2)岁。
(x-2)+ x +(x+2) = 180
3x = 180
x = 60
x+2=60+2=62
x-2=60-2=58
拓展延伸
兄弟三人的年龄是三个连续的偶数。他们的年龄和是180岁,他们三人的年龄分别是多少岁?
老大:60 + 2 = 62(岁)
老二:180÷3=60(岁)
老三:60-2 = 58(岁)
答:老大的年龄是62岁,老二的年龄是60岁,
老三的年龄是58岁。
回顾反思
通过这节课的学习,你有什么收获
