2022-2023学年人教版数学八年级下册16.1二次根式 课件(共24张PPT)
文档属性
| 名称 | 2022-2023学年人教版数学八年级下册16.1二次根式 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
16.1 二次根式
学习目标
1.理解二次根式的概念.
2.掌握二次根式有意义的条件.
3.掌握二次根式的两条重要性质.
重难点
重点:掌握二次根式有意义的条件
难点:掌握二次根式的两条重要性质.
情景导入
(1)5的平方根是______,0的平方根是______,正实数a的平方根是________.
说一说
情景导入
因为v2=gR,而且v一定大于0, 所以第一宇宙速度.
说一说
(2)运用运载火箭发射航天飞船时,火箭必须达到一定的速度(称为第一宇宙速度),才能克服地球的引力,从而将飞船送入环地球运行的轨道.而第一字宙速度与地球半径R之间存在如下关系:v2=gR,其中重力加速度常数g=9.8 m/s2.若已知地球半径R,则第一宇宙速度是多少?
探究新知
我们把形如 (a≥0) 的式子叫作二次根式,根号下的数叫作被开方数.
事实上, (a≥0) 就是a的算术平方根 ,所以二次根式也具备双重非负性.
a可以是数,也可以是式子.
注意
1.二次根式的定义
二次根式具有两个特征
①外貌特征:含有“”.
②内在特征:被开方数a ≥0.
探究新知
典例剖析
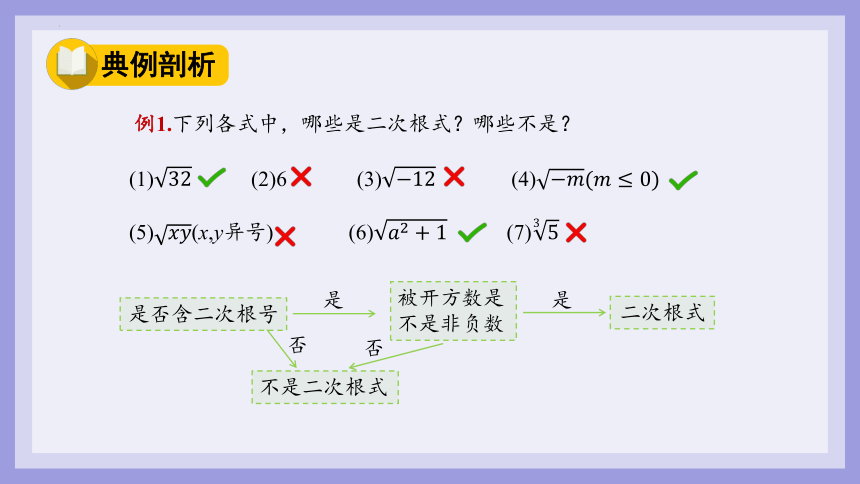
例1.下列各式中,哪些是二次根式?哪些不是?
(1) (2)6 (3) (4)
(5)(x,y异号) (6) (7)
是否含二次根号
被开方数是不是非负数
二次根式
不是二次根式
是
是
否
否
探究新知
二次根式有意义的条件:
二次根式无意义的条件:
被开方数(式)为非负数.
被开方数(式)为负数.
2.二次根式有、无意义的条件
典例剖析
解:由x-1≥0,得 x≥1.
所以当x≥1时, 在实数范围内有意义.
例2.当x是怎样的实数时,二次根式 在实数范围内有意义
针对练习
当x是怎样的实数时,下列各式在实数范围内有意义?
(2)由题意,得3+x≥0,解得x≥-3.
x-1≠0,解得x≠1.
解:(1)由题意,得x-2>0,解得x>2.
所以当x>2时, 在实数范围内有意义.
所以当x≥-3 且x≠1时,在实数范围内有意义.
归纳总结
第三步,求不等式或不等式组的解集即为字母的取值范围.
求式子有意义时字母的取值范围的方法
第一步,明确式子有意义的条件,对于单个的二次根式只需满足被开方数为非负数;对于含有多个二次根式的,则必须满足多个被开方数同时为非负数;对于零指数,则必须满足底数不能为零;对于含有分式的,则还需满足分母不能为零;
第二步,利用式子中所有有意义的条件,建立不等式或不等式组;
探究新知
二次根式的实质是表示一个非负数(或式)的算术平方根.
对于任意一个二次根式我们知道:
(1)a为被开方数,为保证其有意义,可知a≥0;
(2)表示一个数或式的算术平方根,可知≥0.
)
二次根式的
双重非负性
二次根式的被开方数非负
二次根式的值非负
的性质
3.二次根式的重要性质
典例剖析
例2.计算:
(1) (2)
解:(1)
(2)
探究新知
填空:
=________,________,________,
……
根据上述结果猜想,当a≥0时,________.
2
1.2
的性质
a
探究新知
的性质
=a(a ≥0).
(a ≥0) 的性质
一个非负数的算术平方根的平方等于它本身.
任意一个数的平方的算术平方根等于这个数的绝对值.
注意:不要忽略
a≥0这一限制条件.
典例剖析
解:(1)
(2)
例3.计算:
(1) (2)
针对练习
所以
若与|xy3|互为相反数,则x+y的值为( )
A.3 B.9 C.12 D.27
D
根据互为相反数的两数相加得0,
可知+|xy3|=0,
解得即x+y=27.
当堂练习
1. 下列式子中,不属于二次根式的是( )
C
2.式子 有意义的条件是( )
A.x>2 B.x≥2 C.x<2 D.x≤2
3x-6>0
x>2
A
当堂练习
3.当x=____时,二次根式取最小值,其最小值 为______.
0
4.计算:(1) =________;
(2) =________;
(3) =________;
(4) =________ .
3
5
18
a2+1
当堂练习
5.实数a、b在数轴上的对应点如图所示,请你化简:.
=-2a.
a
0
b
解:由数轴可知a<0,b>0,a-b<0,
∴原式= |a|-|b|+|a-b|
=-a-b-(a-b)
当堂练习
=3a+b-c.
6.已知a、b、c是△ABC的三边长,
化简:.
解:∵a、b、c是△ABC的三边长,
∴a+b>c,b+c>a,c+a>b,
∴原式= |a+b+c|- |b+c-a|+ |c-b-a|
= a+b+c-(b+c-a)+(b+a-c)
=a+b+c-b-c+a+b+a-c
小结梳理
二次根式
二次根式的概念
二次根式的表示
二次根式有意义的条件
被开方数≥0
→
性质
应用
16.1 二次根式
学习目标
1.理解二次根式的概念.
2.掌握二次根式有意义的条件.
3.掌握二次根式的两条重要性质.
重难点
重点:掌握二次根式有意义的条件
难点:掌握二次根式的两条重要性质.
情景导入
(1)5的平方根是______,0的平方根是______,正实数a的平方根是________.
说一说
情景导入
因为v2=gR,而且v一定大于0, 所以第一宇宙速度.
说一说
(2)运用运载火箭发射航天飞船时,火箭必须达到一定的速度(称为第一宇宙速度),才能克服地球的引力,从而将飞船送入环地球运行的轨道.而第一字宙速度与地球半径R之间存在如下关系:v2=gR,其中重力加速度常数g=9.8 m/s2.若已知地球半径R,则第一宇宙速度是多少?
探究新知
我们把形如 (a≥0) 的式子叫作二次根式,根号下的数叫作被开方数.
事实上, (a≥0) 就是a的算术平方根 ,所以二次根式也具备双重非负性.
a可以是数,也可以是式子.
注意
1.二次根式的定义
二次根式具有两个特征
①外貌特征:含有“”.
②内在特征:被开方数a ≥0.
探究新知
典例剖析
例1.下列各式中,哪些是二次根式?哪些不是?
(1) (2)6 (3) (4)
(5)(x,y异号) (6) (7)
是否含二次根号
被开方数是不是非负数
二次根式
不是二次根式
是
是
否
否
探究新知
二次根式有意义的条件:
二次根式无意义的条件:
被开方数(式)为非负数.
被开方数(式)为负数.
2.二次根式有、无意义的条件
典例剖析
解:由x-1≥0,得 x≥1.
所以当x≥1时, 在实数范围内有意义.
例2.当x是怎样的实数时,二次根式 在实数范围内有意义
针对练习
当x是怎样的实数时,下列各式在实数范围内有意义?
(2)由题意,得3+x≥0,解得x≥-3.
x-1≠0,解得x≠1.
解:(1)由题意,得x-2>0,解得x>2.
所以当x>2时, 在实数范围内有意义.
所以当x≥-3 且x≠1时,在实数范围内有意义.
归纳总结
第三步,求不等式或不等式组的解集即为字母的取值范围.
求式子有意义时字母的取值范围的方法
第一步,明确式子有意义的条件,对于单个的二次根式只需满足被开方数为非负数;对于含有多个二次根式的,则必须满足多个被开方数同时为非负数;对于零指数,则必须满足底数不能为零;对于含有分式的,则还需满足分母不能为零;
第二步,利用式子中所有有意义的条件,建立不等式或不等式组;
探究新知
二次根式的实质是表示一个非负数(或式)的算术平方根.
对于任意一个二次根式我们知道:
(1)a为被开方数,为保证其有意义,可知a≥0;
(2)表示一个数或式的算术平方根,可知≥0.
)
二次根式的
双重非负性
二次根式的被开方数非负
二次根式的值非负
的性质
3.二次根式的重要性质
典例剖析
例2.计算:
(1) (2)
解:(1)
(2)
探究新知
填空:
=________,________,________,
……
根据上述结果猜想,当a≥0时,________.
2
1.2
的性质
a
探究新知
的性质
=a(a ≥0).
(a ≥0) 的性质
一个非负数的算术平方根的平方等于它本身.
任意一个数的平方的算术平方根等于这个数的绝对值.
注意:不要忽略
a≥0这一限制条件.
典例剖析
解:(1)
(2)
例3.计算:
(1) (2)
针对练习
所以
若与|xy3|互为相反数,则x+y的值为( )
A.3 B.9 C.12 D.27
D
根据互为相反数的两数相加得0,
可知+|xy3|=0,
解得即x+y=27.
当堂练习
1. 下列式子中,不属于二次根式的是( )
C
2.式子 有意义的条件是( )
A.x>2 B.x≥2 C.x<2 D.x≤2
3x-6>0
x>2
A
当堂练习
3.当x=____时,二次根式取最小值,其最小值 为______.
0
4.计算:(1) =________;
(2) =________;
(3) =________;
(4) =________ .
3
5
18
a2+1
当堂练习
5.实数a、b在数轴上的对应点如图所示,请你化简:.
=-2a.
a
0
b
解:由数轴可知a<0,b>0,a-b<0,
∴原式= |a|-|b|+|a-b|
=-a-b-(a-b)
当堂练习
=3a+b-c.
6.已知a、b、c是△ABC的三边长,
化简:.
解:∵a、b、c是△ABC的三边长,
∴a+b>c,b+c>a,c+a>b,
∴原式= |a+b+c|- |b+c-a|+ |c-b-a|
= a+b+c-(b+c-a)+(b+a-c)
=a+b+c-b-c+a+b+a-c
小结梳理
二次根式
二次根式的概念
二次根式的表示
二次根式有意义的条件
被开方数≥0
→
性质
应用
