6.1~6.2平面向量的概念与运算(小结课) 课件(共49张PPT)
文档属性
| 名称 | 6.1~6.2平面向量的概念与运算(小结课) 课件(共49张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 00:00:00 | ||
图片预览









文档简介
(共49张PPT)
必修 第二册 第六章 平面向量
6.1~6.2
平面向量的概念与运算(小结课)
(1)向量与数量
既有大小,又有方向的量叫做向量(物理学中称为矢量);
只有大小,没有方向的量叫做数量(物理学中称为标量).
注意:
数量只有大小,是一个代数量,可以进行代数运算、能比较大小;向量具有大小和方向这双重要素,由于方向不能比较大小,故向量不能比较大小.
知识点1 平面向量的概念
(3)相等向量:长度相等且方向相同的向量叫相等向量.
a
b
c
表示为:a =b=c
A B =A B =A B =A B
A
B
A
B
A
B
A
B
2.零向量与零向量相等
3.任意两个相等的非零向量,都可用同一条有向
线段来表示,并且与有向线段的起点无关.
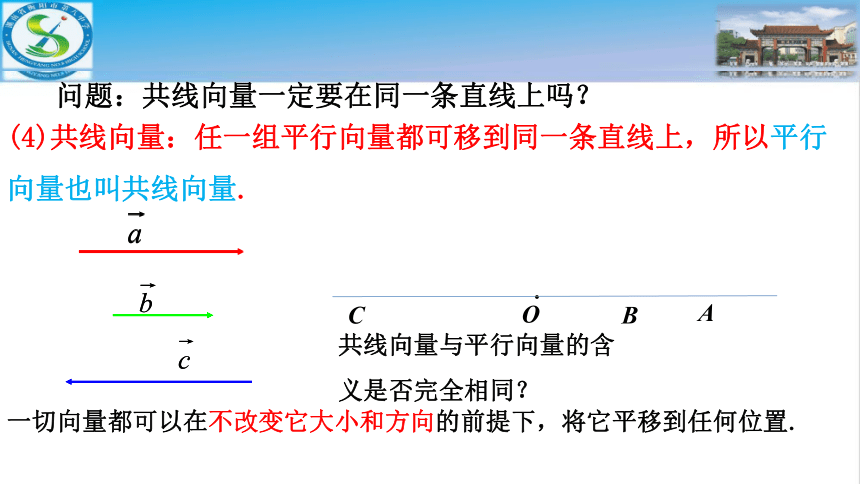
问题:共线向量一定要在同一条直线上吗?
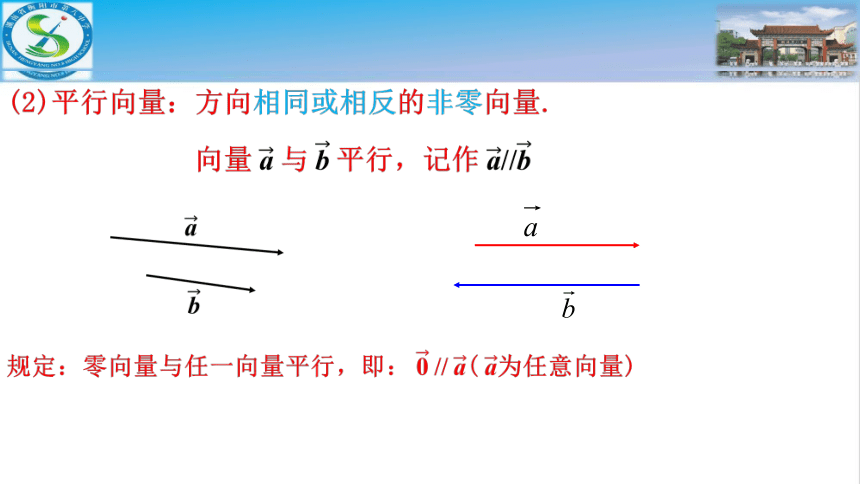
(4)共线向量:任一组平行向量都可移到同一条直线上,所以平行向量也叫共线向量.
O
A
B
C
一切向量都可以在不改变它大小和方向的前提下,将它平移到任何位置.
共线向量与平行向量的含
义是否完全相同?
1.向量加法的定义及运算法则
平面向量的加法运算
知识点2
两个向量和
a+b
0+a
a
2.三角不等式:|a+b|≤___________,当且仅当a,b方向相同时等号成立.
3.向量加法的运算律
运算律 结合律 a+b=_______
交换律 (a+b)+c=____________
|a|+|b|
b+a
a+(b+c)
在某地抗震救灾中,一架飞机从A地按北偏东35°的方向飞行800 km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行800 km送往C地医院,求这架飞机飞行的路程及两次位移的和.
[分析] 解答本题首先正确画出方位图,再根据图形借助于向量求解.
题型1 向量加法的实际应用
典例 1
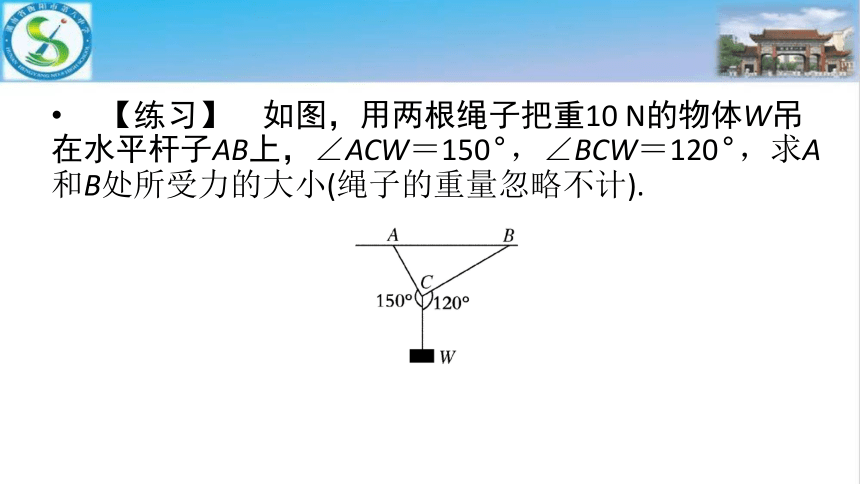
【练习】 如图,用两根绳子把重10 N的物体W吊在水平杆子AB上,∠ACW=150°,∠BCW=120°,求A和B处所受力的大小(绳子的重量忽略不计).
向量的减法
知识点3
相反向量
终点
终点
①④
典例 4
错误使用向量的减法法则
向量的数乘运算
知识点4
向量
数乘
|λ||a|
相同
相反
2.向量数乘的运算律
设λ,μ为实数,那么
(1)λ(μa)=________.
(2)(λ+μ)a=_________.
(3)λ(a+b)=_________.
特别地,我们有(-λ)a=-λa=λ(-a),λ(a-b)=λa-λb.
(λμ)a
λa+μa
λa+λb
3.向量的线性运算
向量的加、减、数乘运算统称为向量的线性运算.向量线性运算的结果仍是向量.对于任意向量a,b,以及任意实数λ,μ1,μ2,恒有λ(μ1a±μ2b)=_____________.
λμ1a±λμ2b
向量a(a≠0)与b共线的充要条件是:存在唯一一个实数λ,使________.
向量共线定理
b=λa
题型 用向量的线性运算表示未知向量
典例 2
题型 共线向量定理及其应用
典例 3
向量的数量积
知识点5
0
π
0
π
a⊥b
2.向量的数量积
条件 非零向量a与b,它们的夹角为θ
结论 数量______________叫做向量a与b的数量积(或内积)
记法 向量a与b的数量积记作a·b,即a·b=______________
规定 零向量与任一向量的数量积为____
|a||b|cos θ
|a||b|cos θ
0
向量a在向量b上
|a|cos θe
1.数量积的性质
设a,b是两个非零向量,它们的夹角是θ,e是与b方向相同的单位向量,则
(1)a·e=e·a=___________.
(2)a⊥b __________.
(3)当a,b同向时,a·b=_________;当a,b反向时,a·b=___________.特别地,a·a=_______或|a|=_____.
(4)|a·b|≤_________.
(5)cos θ=_____.
向量的数量积的性质及运算律
知识点2
|a|cos θ
a·b=0
|a||b|
-|a||b|
|a|2
|a||b|
2.数量积的运算律
对于向量a,b,c和实数λ,有
(1)a·b=_______(交换律).
(2)(λa)·b=__________=__________(结合律).
(3)(a+b)·c=_____________(分配律).
b·a
λ(a·b)
a·(λb)
a·c+b·c
(1)已知|a|=2,|b|=3,a与b的夹角为120°,试求:
①a·b;
②(a+b)·(a-b);
③(2a-b)·(a+3b).
题型 平面向量的数量积
典例
[分析] 灵活应用a2=|a|2求向量的模.
题型 利用数量积解决求模问题
典例 2
(1)已知向量a,b满足(a+2b)·(a-b)=-6,且|a|=1,|b|=2,则a与b的夹角为_____.
(2)已知|a|=3,|b|=2,向量a,b的夹角为60°,c=3a+5b,d=ma-3b,求当m为何值时,c与d垂直?
[分析] (1)由向量的运算律结合向量的夹角公式求解.
(2)根据两向量垂直的充要条件建立关于m的方程进行求解.
题型 两向量的夹角和垂直问题
典例 3
典例 4
忽略向量共线的情形致错
A
必修 第二册 第六章 平面向量
6.1~6.2
平面向量的概念与运算(小结课)
(1)向量与数量
既有大小,又有方向的量叫做向量(物理学中称为矢量);
只有大小,没有方向的量叫做数量(物理学中称为标量).
注意:
数量只有大小,是一个代数量,可以进行代数运算、能比较大小;向量具有大小和方向这双重要素,由于方向不能比较大小,故向量不能比较大小.
知识点1 平面向量的概念
(3)相等向量:长度相等且方向相同的向量叫相等向量.
a
b
c
表示为:a =b=c
A B =A B =A B =A B
A
B
A
B
A
B
A
B
2.零向量与零向量相等
3.任意两个相等的非零向量,都可用同一条有向
线段来表示,并且与有向线段的起点无关.
问题:共线向量一定要在同一条直线上吗?
(4)共线向量:任一组平行向量都可移到同一条直线上,所以平行向量也叫共线向量.
O
A
B
C
一切向量都可以在不改变它大小和方向的前提下,将它平移到任何位置.
共线向量与平行向量的含
义是否完全相同?
1.向量加法的定义及运算法则
平面向量的加法运算
知识点2
两个向量和
a+b
0+a
a
2.三角不等式:|a+b|≤___________,当且仅当a,b方向相同时等号成立.
3.向量加法的运算律
运算律 结合律 a+b=_______
交换律 (a+b)+c=____________
|a|+|b|
b+a
a+(b+c)
在某地抗震救灾中,一架飞机从A地按北偏东35°的方向飞行800 km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行800 km送往C地医院,求这架飞机飞行的路程及两次位移的和.
[分析] 解答本题首先正确画出方位图,再根据图形借助于向量求解.
题型1 向量加法的实际应用
典例 1
【练习】 如图,用两根绳子把重10 N的物体W吊在水平杆子AB上,∠ACW=150°,∠BCW=120°,求A和B处所受力的大小(绳子的重量忽略不计).
向量的减法
知识点3
相反向量
终点
终点
①④
典例 4
错误使用向量的减法法则
向量的数乘运算
知识点4
向量
数乘
|λ||a|
相同
相反
2.向量数乘的运算律
设λ,μ为实数,那么
(1)λ(μa)=________.
(2)(λ+μ)a=_________.
(3)λ(a+b)=_________.
特别地,我们有(-λ)a=-λa=λ(-a),λ(a-b)=λa-λb.
(λμ)a
λa+μa
λa+λb
3.向量的线性运算
向量的加、减、数乘运算统称为向量的线性运算.向量线性运算的结果仍是向量.对于任意向量a,b,以及任意实数λ,μ1,μ2,恒有λ(μ1a±μ2b)=_____________.
λμ1a±λμ2b
向量a(a≠0)与b共线的充要条件是:存在唯一一个实数λ,使________.
向量共线定理
b=λa
题型 用向量的线性运算表示未知向量
典例 2
题型 共线向量定理及其应用
典例 3
向量的数量积
知识点5
0
π
0
π
a⊥b
2.向量的数量积
条件 非零向量a与b,它们的夹角为θ
结论 数量______________叫做向量a与b的数量积(或内积)
记法 向量a与b的数量积记作a·b,即a·b=______________
规定 零向量与任一向量的数量积为____
|a||b|cos θ
|a||b|cos θ
0
向量a在向量b上
|a|cos θe
1.数量积的性质
设a,b是两个非零向量,它们的夹角是θ,e是与b方向相同的单位向量,则
(1)a·e=e·a=___________.
(2)a⊥b __________.
(3)当a,b同向时,a·b=_________;当a,b反向时,a·b=___________.特别地,a·a=_______或|a|=_____.
(4)|a·b|≤_________.
(5)cos θ=_____.
向量的数量积的性质及运算律
知识点2
|a|cos θ
a·b=0
|a||b|
-|a||b|
|a|2
|a||b|
2.数量积的运算律
对于向量a,b,c和实数λ,有
(1)a·b=_______(交换律).
(2)(λa)·b=__________=__________(结合律).
(3)(a+b)·c=_____________(分配律).
b·a
λ(a·b)
a·(λb)
a·c+b·c
(1)已知|a|=2,|b|=3,a与b的夹角为120°,试求:
①a·b;
②(a+b)·(a-b);
③(2a-b)·(a+3b).
题型 平面向量的数量积
典例
[分析] 灵活应用a2=|a|2求向量的模.
题型 利用数量积解决求模问题
典例 2
(1)已知向量a,b满足(a+2b)·(a-b)=-6,且|a|=1,|b|=2,则a与b的夹角为_____.
(2)已知|a|=3,|b|=2,向量a,b的夹角为60°,c=3a+5b,d=ma-3b,求当m为何值时,c与d垂直?
[分析] (1)由向量的运算律结合向量的夹角公式求解.
(2)根据两向量垂直的充要条件建立关于m的方程进行求解.
题型 两向量的夹角和垂直问题
典例 3
典例 4
忽略向量共线的情形致错
A
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
