6.4 专题 竖直平面内的圆周运动 课件(共16张PPT)高一下学期物理人教版(2019)必修第二册
文档属性
| 名称 | 6.4 专题 竖直平面内的圆周运动 课件(共16张PPT)高一下学期物理人教版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-08 22:18:54 | ||
图片预览





文档简介
(共16张PPT)
竖直平面内的圆周运动
惊险刺激的过山车
水流星表演
1、过山车在竖直圆形轨道上运动为什么不会掉下来?
2、水流星中的水在最高点为什么不会撒出来?
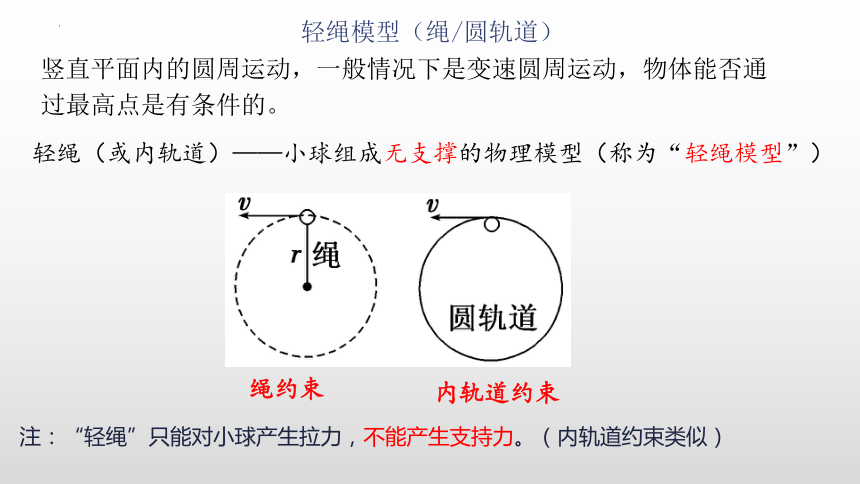
竖直平面内的圆周运动,一般情况下是变速圆周运动,物体能否通过最高点是有条件的。
轻绳(或内轨道)——小球组成无支撑的物理模型(称为“轻绳模型”)
绳约束
内轨道约束
注:“轻绳”只能对小球产生拉力,不能产生支持力。(内轨道约束类似)
轻绳模型(绳/圆轨道)
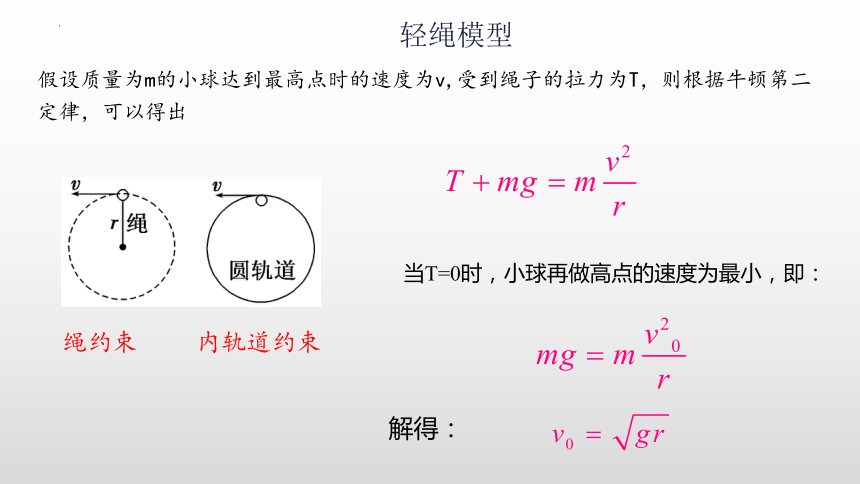
绳约束
内轨道约束
假设质量为m的小球达到最高点时的速度为v,受到绳子的拉力为T,则根据牛顿第二定律,可以得出
当T=0时,小球再做高点的速度为最小,即:
解得:
轻绳模型
小球在最高点时,绳子恰好对小球没有力的作用
(1)小球恰好能达到最高点的临界条件是:
(2)小球恰好能通过最高点的条件是 :
当
绳子有拉力(轨道对球有压力)。
(3)当 ,小球还未达到最高点就离开轨道。
o
R
轻绳
G=mg
V2
F拉
典例:一质量为0.5kg的小球,用长为0.4m细绳拴住,在竖直平面内做圆周运动(g取10m/s2),求:
(1)若过最高点时的速度为4m/s,此时小球角速度多大?
(2)若过最高点时绳的拉力刚好为零,此时小球速度大小?
(3)若过最低点时的速度为6m/s,此时绳的拉力大小?
50N
典例:如图所示,质量为0.1kg的木桶内盛水0.4kg,用40cm的绳子系住桶,并使它在竖直平面内做圆周运动。(桶可视为质点,取g=10m/s2)
(1)要使水不洒出,木桶在最高点的速度至少多大?
(2)如果通过最低点时速度大小10m/s,求最低点时桶底对水的支持力大小。
(1)2m/s;(2)104N
轻杆(或管道)——小球组成有支撑的物理模型(称为“轻杆模型”)
杆约束
管道约束
注:“轻杆”既能对小球产生拉力,也能产生支持力。(管道约束类似)
轻杆模型(杆/管道)
球过最高点时,设轻杆对小球产生的弹力FN方向向上。
由牛顿第二定律得:
故
由此可知:弹力FN的大小和方向随着经最高点时速度v的大小的变化而变化
轻杆模型
(1)小球恰好能达到最高点的临界条件是: ,
故而V0>0就可以通过最高点。
(2) 当 ,FN为支持力,方向竖直向上,且随着速度增大而减小。
(3)当 ,FN=0
(4)当 ,FN为拉力,方向竖直向下,且随着速度增大而增大。
典例:(多选)如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为R,小球半径为r,则下列说法中正确的是( )
A. 小球通过最高点时的最小速度vmin=
B. 小球通过最高点时的最小速度vmin=0
C. 小球在水平线ab以下的管道中运动时,内侧管壁对小球
一定无作用力
D. 小球在水平线ab以上的管道中运动时,外侧管壁对小球一定有作用力
BC
物理情景 最高点无支撑 最高点有支撑
实例 球与绳连接、水流星、沿内轨道运动的“过山车”等 球与杆连接、球在光滑
管道中运动等
图示
受力 特征 物体受到的弹力方向: 向下或等于零 物体受到的弹力方向:
向下、等于零或向上
典例:如图所示,一质量为m=0.5kg的小球从一段半径为R=1m的圆弧轨道上的A点由静止下滑到轨道末端B后水平抛出,经t=0.4s落到水平地面上,速度与水平面成45°角.不计空气阻力,g取10m/s2.求:
(1)小球在空中飞行的位移大小;
(2)小球经过轨道末端时对轨道的压力.
结
束
竖直平面内的圆周运动
惊险刺激的过山车
水流星表演
1、过山车在竖直圆形轨道上运动为什么不会掉下来?
2、水流星中的水在最高点为什么不会撒出来?
竖直平面内的圆周运动,一般情况下是变速圆周运动,物体能否通过最高点是有条件的。
轻绳(或内轨道)——小球组成无支撑的物理模型(称为“轻绳模型”)
绳约束
内轨道约束
注:“轻绳”只能对小球产生拉力,不能产生支持力。(内轨道约束类似)
轻绳模型(绳/圆轨道)
绳约束
内轨道约束
假设质量为m的小球达到最高点时的速度为v,受到绳子的拉力为T,则根据牛顿第二定律,可以得出
当T=0时,小球再做高点的速度为最小,即:
解得:
轻绳模型
小球在最高点时,绳子恰好对小球没有力的作用
(1)小球恰好能达到最高点的临界条件是:
(2)小球恰好能通过最高点的条件是 :
当
绳子有拉力(轨道对球有压力)。
(3)当 ,小球还未达到最高点就离开轨道。
o
R
轻绳
G=mg
V2
F拉
典例:一质量为0.5kg的小球,用长为0.4m细绳拴住,在竖直平面内做圆周运动(g取10m/s2),求:
(1)若过最高点时的速度为4m/s,此时小球角速度多大?
(2)若过最高点时绳的拉力刚好为零,此时小球速度大小?
(3)若过最低点时的速度为6m/s,此时绳的拉力大小?
50N
典例:如图所示,质量为0.1kg的木桶内盛水0.4kg,用40cm的绳子系住桶,并使它在竖直平面内做圆周运动。(桶可视为质点,取g=10m/s2)
(1)要使水不洒出,木桶在最高点的速度至少多大?
(2)如果通过最低点时速度大小10m/s,求最低点时桶底对水的支持力大小。
(1)2m/s;(2)104N
轻杆(或管道)——小球组成有支撑的物理模型(称为“轻杆模型”)
杆约束
管道约束
注:“轻杆”既能对小球产生拉力,也能产生支持力。(管道约束类似)
轻杆模型(杆/管道)
球过最高点时,设轻杆对小球产生的弹力FN方向向上。
由牛顿第二定律得:
故
由此可知:弹力FN的大小和方向随着经最高点时速度v的大小的变化而变化
轻杆模型
(1)小球恰好能达到最高点的临界条件是: ,
故而V0>0就可以通过最高点。
(2) 当 ,FN为支持力,方向竖直向上,且随着速度增大而减小。
(3)当 ,FN=0
(4)当 ,FN为拉力,方向竖直向下,且随着速度增大而增大。
典例:(多选)如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为R,小球半径为r,则下列说法中正确的是( )
A. 小球通过最高点时的最小速度vmin=
B. 小球通过最高点时的最小速度vmin=0
C. 小球在水平线ab以下的管道中运动时,内侧管壁对小球
一定无作用力
D. 小球在水平线ab以上的管道中运动时,外侧管壁对小球一定有作用力
BC
物理情景 最高点无支撑 最高点有支撑
实例 球与绳连接、水流星、沿内轨道运动的“过山车”等 球与杆连接、球在光滑
管道中运动等
图示
受力 特征 物体受到的弹力方向: 向下或等于零 物体受到的弹力方向:
向下、等于零或向上
典例:如图所示,一质量为m=0.5kg的小球从一段半径为R=1m的圆弧轨道上的A点由静止下滑到轨道末端B后水平抛出,经t=0.4s落到水平地面上,速度与水平面成45°角.不计空气阻力,g取10m/s2.求:
(1)小球在空中飞行的位移大小;
(2)小球经过轨道末端时对轨道的压力.
结
束
