6.4.3.2正弦定理 课件(共20张PPT)
文档属性
| 名称 | 6.4.3.2正弦定理 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 319.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 22:08:52 | ||
图片预览



文档简介
(共20张PPT)
6.4 平面向量的应用
6.4.3 余弦定理、正弦定理
第2课时 正弦定理
问题提出
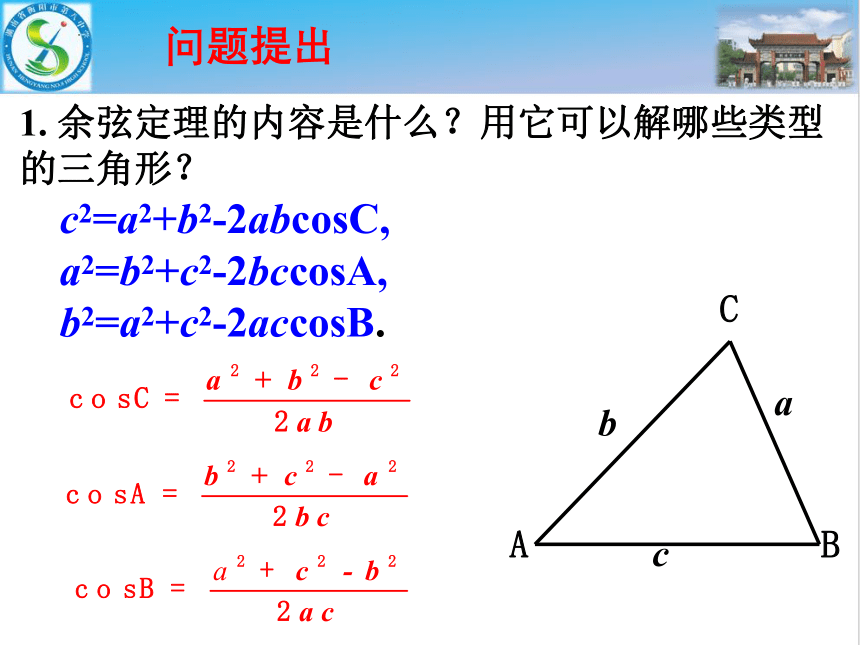
1. 余弦定理的内容是什么?用它可以解哪些类型的三角形?
A
B
C
a
b
c
c2=a2+b2-2abcosC,
a2=b2+c2-2bccosA,
b2=a2+c2-2accosB.
问题提出
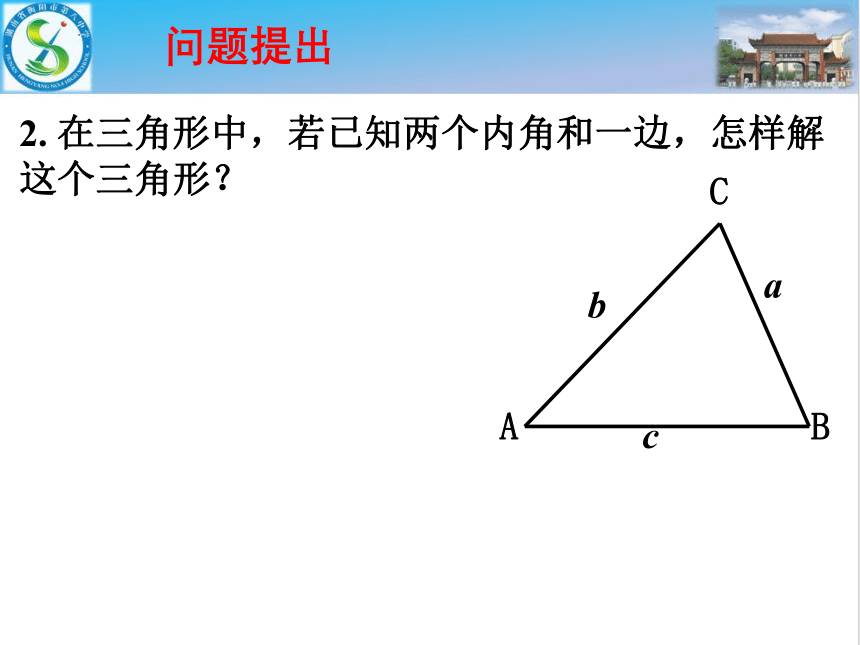
2. 在三角形中,若已知两个内角和一边,怎样解这个三角形?
A
B
C
a
b
c
探究:正弦定理及推导
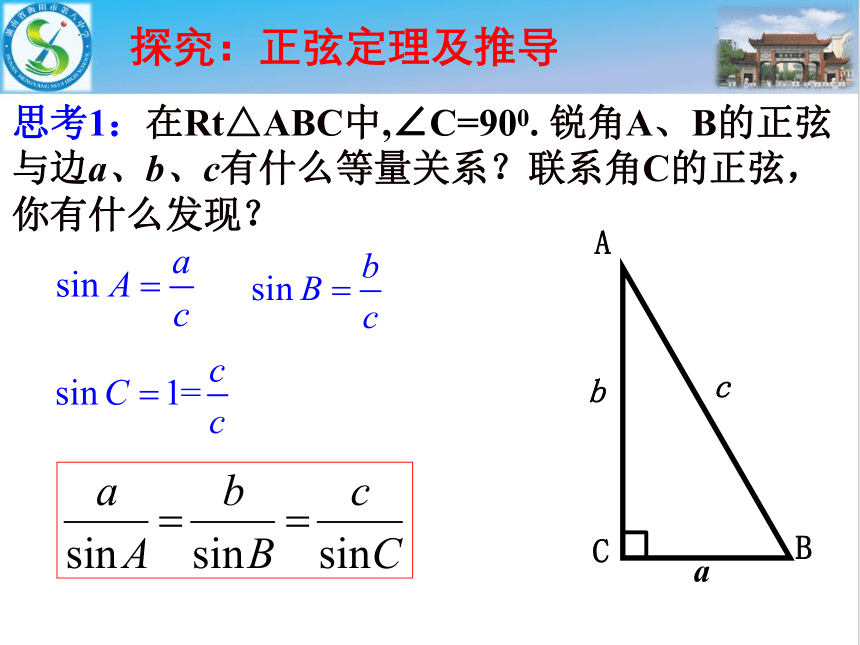
思考1:在Rt△ABC中,∠C=900. 锐角A、B的正弦与边a、b、c有什么等量关系?联系角C的正弦,你有什么发现?
C
B
A
a
b
c
探究:正弦定理及推导
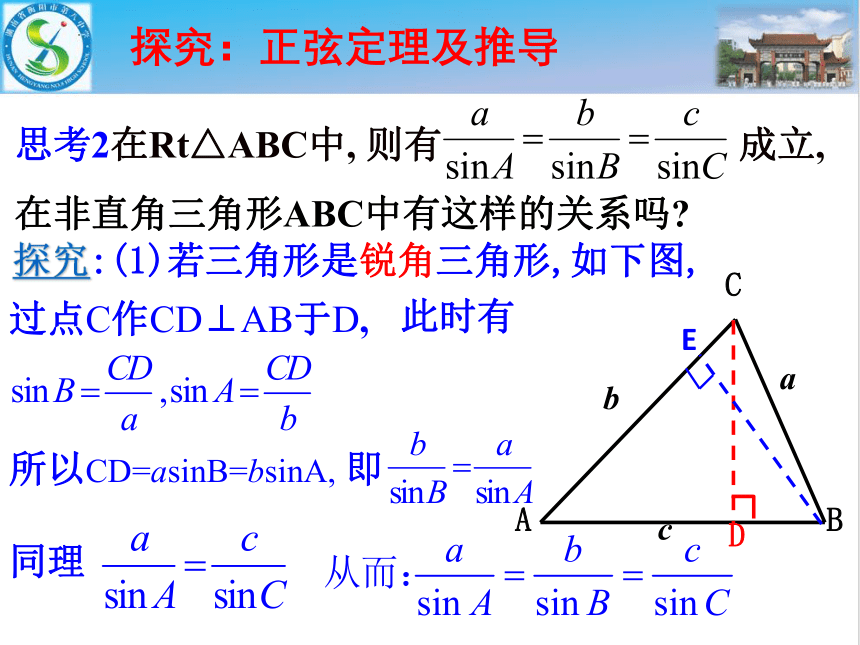
思考2在Rt△ABC中, 则有 成立,在非直角三角形ABC中有这样的关系吗
A
B
C
a
b
c
探究:(1)若三角形是锐角三角形,如下图,
过点C作CD⊥AB于D,
D
此时有
所以CD=asinB=bsinA, 即
同理
E
探究:正弦定理及推导
且
仿(1)可得
D
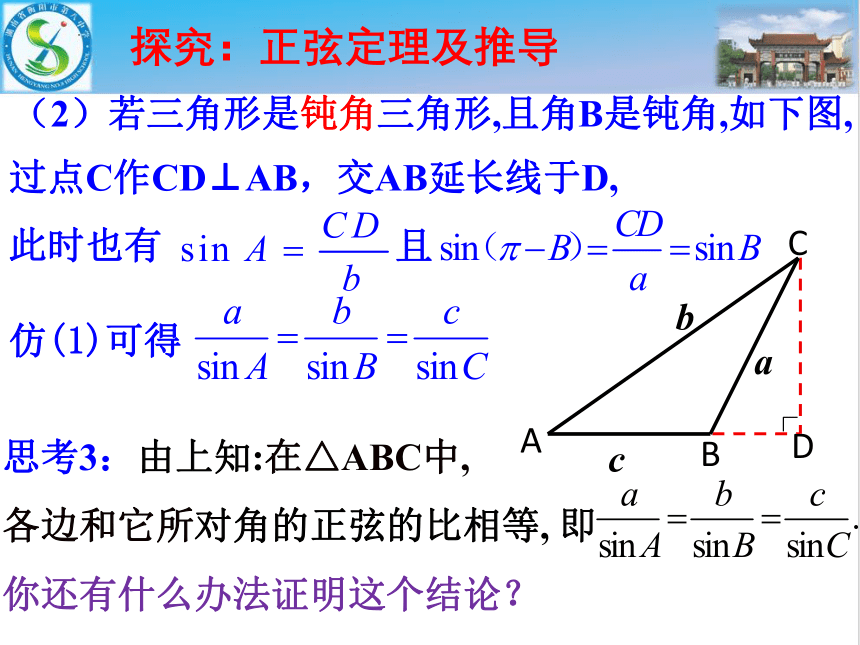
(2)若三角形是钝角三角形,且角B是钝角,如下图,
此时也有
过点C作CD⊥AB,交AB延长线于D,
B
C
b
a
A
c
思考3:由上知:在△ABC中,
各边和它所对角的正弦的比相等, 即
你还有什么办法证明这个结论?
探究:正弦定理及推导
证明2:
O
D
c
b
a
C
B
A
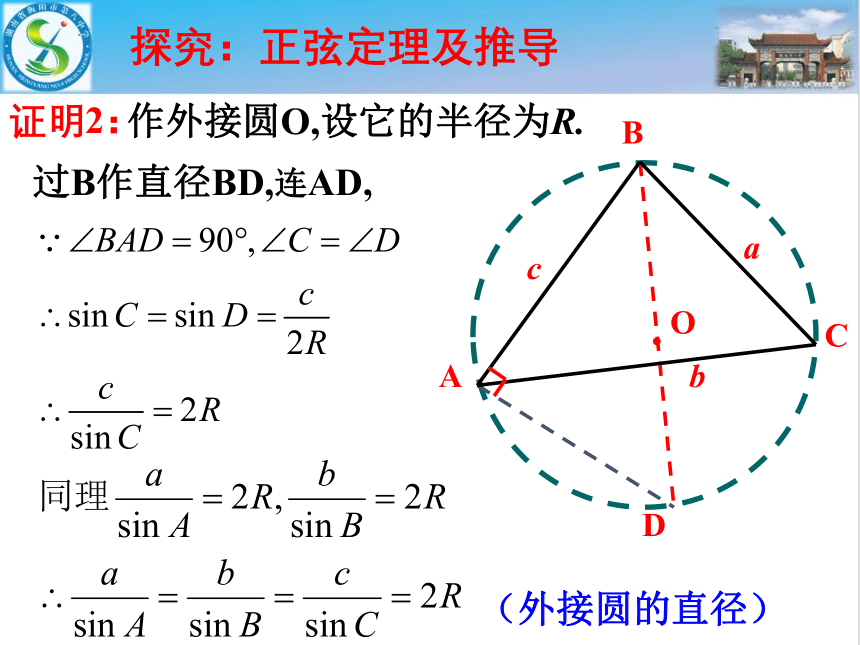
作外接圆O,设它的半径为R.
过B作直径BD,连AD,
(外接圆的直径)
探究:正弦定理及推导
A
B
C
a
b
c
证明3:
设i是与AB垂直的单位向量.
思考4:在△ABC中, 各边和它所对角的正弦的比相等,即
这个结论称为正弦定理. 那么利用正弦定理可以解决一些怎样的解三角形问题?
①已知两角和一边,求其他角和边.
②已知两边和其中一边的对角,求另一边的对角,进而可求其他的边和角.
探究:正弦定理
探究:运用正弦定理解三角形
已知两角及一边解三角形
例1 在△ABC中,已知c =10, A=45。, C=30。,
解三角形.
B
A
C
a
b
c
解:
B=1800-450-300=1050
由正弦定理得
探究:运用正弦定理解三角形
已知两边及其中一边的对角
解:由正弦定理
得
所以
B=60°,
或B=120°
当B=60°时
C=90 °,
例2 在△ABC中,已知a=16, b= , A=30°.
解三角形.
C=30°,
当B=120°时
B
16
300
A
B
C
16
3
16
变式训练
1.在△ABC中,已知B=30°,C=105°,b=4,
解三角形.
解 因为B=30°,C=105°,
所以A=180°-(B+C)=180°-(30°+105°)=45°.
变式训练
2.在△ABC中,已知c= ,A=45°,a=2,
解三角形.
∵0°延伸探究
若把本例中的条件“A=45°”改为“C=45°”,
则角A有几个值?
在△ABC中,已知 a, b, A,解三角形。若b, A为定值,当a满足什么条件时,有两解、一解,可能无解吗?
D
A
B
C
a
b
c
结论探究:
(1)当a(2)当a=bsinA或a≥b时, 有且只有一解;
(3)当bsinA1.当A为锐角时:
2.当A为直角或钝角时:
(1)当a≤b时,无解;
(2)当a>b时,有且只有一解;
反思拓展:
探究:用正弦定理定三角形形状
例3在△ABC中,已知 ,且sin2A+sin2B
=sin2C.求证:△ABC为等腰直角三角形.
∴a2=b2即a=b,
又∵sin2A+sin2B=sin2C,
∴△ABC为等腰直角三角形.
∴a2+b2=c2,
变式训练
在△ABC中,已知2sin Acos B=sin C,试判断
△ABC的形状.
解析 方法一 (利用边的关系进行判断)
由正弦定理和余弦定理,
即a2+c2-b2=c2,即a2=b2,故a=b.
变式训练
在△ABC中,已知2sin Acos B=sin C,试判断
△ABC的形状.
解析 方法二 (利用角的关系进行判断)
因为在△ABC中,A+B+C=π,
即C=π-(A+B),所以sin C=sin(A+B).
由2sin Acos B=sin C=sin(A+B),
得2sin Acos B=sin Acos B+cos Asin B,
即sin Acos B-cos Asin B=0,所以sin(A-B)=0.
因为-π所以△ABC是等腰三角形.
归纳总结
(2)已知两边和一边的对角解三角形时,可能
有一解、两解、无解的情况, 注意具体问题
具体分析.
1.正弦定理:
=
2R
A
B
C
a
b
c
2.运用余弦定理解三角形
(1)已知两角及一边解三角形
作业布置
1. P48 练习1, 2, 3.
2.基础训练 P50
6.4 平面向量的应用
6.4.3 余弦定理、正弦定理
第2课时 正弦定理
问题提出
1. 余弦定理的内容是什么?用它可以解哪些类型的三角形?
A
B
C
a
b
c
c2=a2+b2-2abcosC,
a2=b2+c2-2bccosA,
b2=a2+c2-2accosB.
问题提出
2. 在三角形中,若已知两个内角和一边,怎样解这个三角形?
A
B
C
a
b
c
探究:正弦定理及推导
思考1:在Rt△ABC中,∠C=900. 锐角A、B的正弦与边a、b、c有什么等量关系?联系角C的正弦,你有什么发现?
C
B
A
a
b
c
探究:正弦定理及推导
思考2在Rt△ABC中, 则有 成立,在非直角三角形ABC中有这样的关系吗
A
B
C
a
b
c
探究:(1)若三角形是锐角三角形,如下图,
过点C作CD⊥AB于D,
D
此时有
所以CD=asinB=bsinA, 即
同理
E
探究:正弦定理及推导
且
仿(1)可得
D
(2)若三角形是钝角三角形,且角B是钝角,如下图,
此时也有
过点C作CD⊥AB,交AB延长线于D,
B
C
b
a
A
c
思考3:由上知:在△ABC中,
各边和它所对角的正弦的比相等, 即
你还有什么办法证明这个结论?
探究:正弦定理及推导
证明2:
O
D
c
b
a
C
B
A
作外接圆O,设它的半径为R.
过B作直径BD,连AD,
(外接圆的直径)
探究:正弦定理及推导
A
B
C
a
b
c
证明3:
设i是与AB垂直的单位向量.
思考4:在△ABC中, 各边和它所对角的正弦的比相等,即
这个结论称为正弦定理. 那么利用正弦定理可以解决一些怎样的解三角形问题?
①已知两角和一边,求其他角和边.
②已知两边和其中一边的对角,求另一边的对角,进而可求其他的边和角.
探究:正弦定理
探究:运用正弦定理解三角形
已知两角及一边解三角形
例1 在△ABC中,已知c =10, A=45。, C=30。,
解三角形.
B
A
C
a
b
c
解:
B=1800-450-300=1050
由正弦定理得
探究:运用正弦定理解三角形
已知两边及其中一边的对角
解:由正弦定理
得
所以
B=60°,
或B=120°
当B=60°时
C=90 °,
例2 在△ABC中,已知a=16, b= , A=30°.
解三角形.
C=30°,
当B=120°时
B
16
300
A
B
C
16
3
16
变式训练
1.在△ABC中,已知B=30°,C=105°,b=4,
解三角形.
解 因为B=30°,C=105°,
所以A=180°-(B+C)=180°-(30°+105°)=45°.
变式训练
2.在△ABC中,已知c= ,A=45°,a=2,
解三角形.
∵0°
若把本例中的条件“A=45°”改为“C=45°”,
则角A有几个值?
在△ABC中,已知 a, b, A,解三角形。若b, A为定值,当a满足什么条件时,有两解、一解,可能无解吗?
D
A
B
C
a
b
c
结论探究:
(1)当a
(3)当bsinA
2.当A为直角或钝角时:
(1)当a≤b时,无解;
(2)当a>b时,有且只有一解;
反思拓展:
探究:用正弦定理定三角形形状
例3在△ABC中,已知 ,且sin2A+sin2B
=sin2C.求证:△ABC为等腰直角三角形.
∴a2=b2即a=b,
又∵sin2A+sin2B=sin2C,
∴△ABC为等腰直角三角形.
∴a2+b2=c2,
变式训练
在△ABC中,已知2sin Acos B=sin C,试判断
△ABC的形状.
解析 方法一 (利用边的关系进行判断)
由正弦定理和余弦定理,
即a2+c2-b2=c2,即a2=b2,故a=b.
变式训练
在△ABC中,已知2sin Acos B=sin C,试判断
△ABC的形状.
解析 方法二 (利用角的关系进行判断)
因为在△ABC中,A+B+C=π,
即C=π-(A+B),所以sin C=sin(A+B).
由2sin Acos B=sin C=sin(A+B),
得2sin Acos B=sin Acos B+cos Asin B,
即sin Acos B-cos Asin B=0,所以sin(A-B)=0.
因为-π
归纳总结
(2)已知两边和一边的对角解三角形时,可能
有一解、两解、无解的情况, 注意具体问题
具体分析.
1.正弦定理:
=
2R
A
B
C
a
b
c
2.运用余弦定理解三角形
(1)已知两角及一边解三角形
作业布置
1. P48 练习1, 2, 3.
2.基础训练 P50
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
