6.5垂直关系 第4课时 课件(共20张PPT)
文档属性
| 名称 | 6.5垂直关系 第4课时 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 403.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 22:10:14 | ||
图片预览




文档简介
(共17张PPT)
6.5 垂直关系
第4课时
导入新课
问题1 在过程建设中,建筑工人用一端系有铅锤的线来检查墙面与地面是否垂直,即若紧贴墙面的铅垂的线垂直地面,则确定墙面与地面垂直,否则不垂直,“紧贴墙面的线”这句话的实质意义是什么?
此线在墙所在的平面内,即平面过另一平面的垂线,则两平面垂直.
新知探究
垂直.
问题3 若要判断两平面是否垂直,根据问题2能否得出一个方法?
可以,
只需在一平面内找一直线垂直于另一平面即可.
问题2 当直线与平面垂直时,过此直线可作无数个平面,那么这些平面与已知平面有何关系?
新知探究
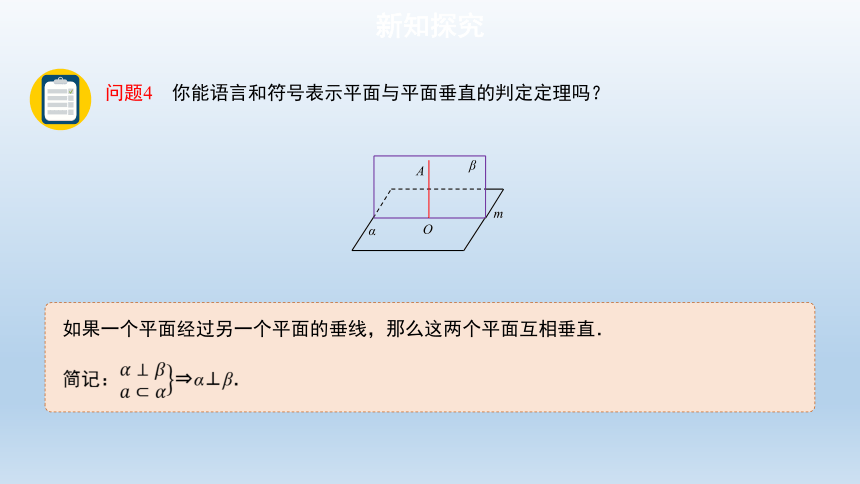
问题4 你能语言和符号表示平面与平面垂直的判定定理吗?
如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直.
简记: α⊥β.
α
β
m
A
O
新知探究
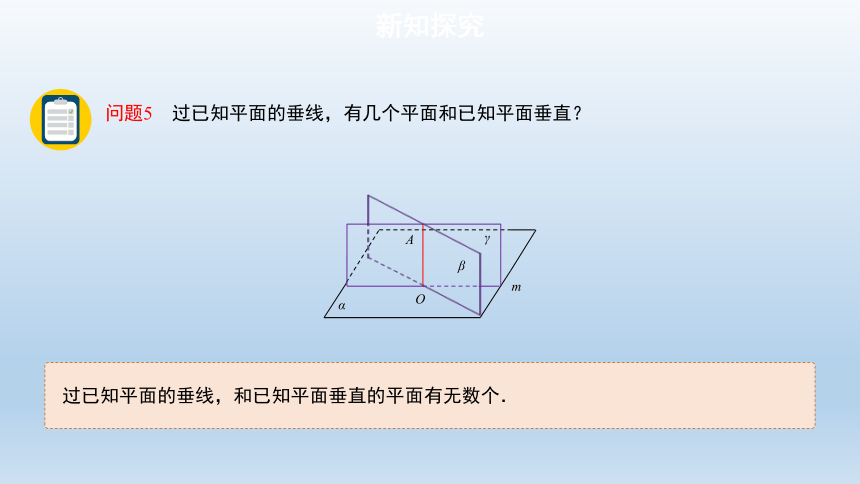
问题5 过已知平面的垂线,有几个平面和已知平面垂直?
过已知平面的垂线,和已知平面垂直的平面有无数个.
α
β
m
A
O
γ
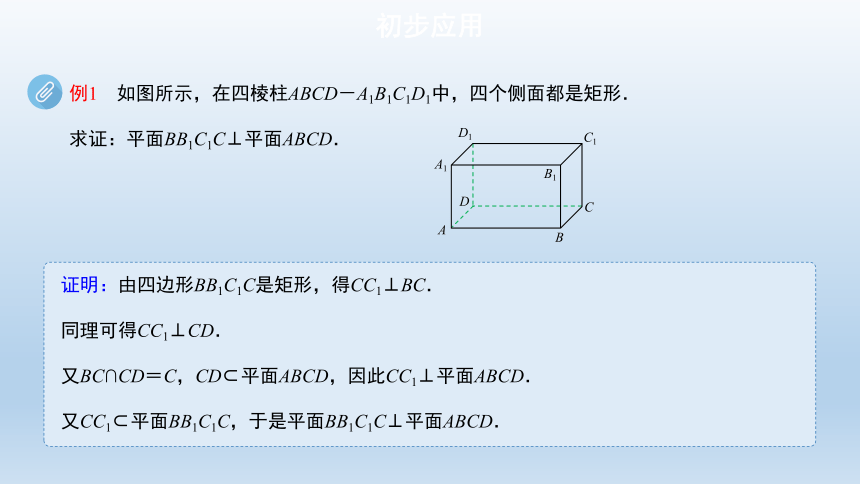
例1 如图所示,在四棱柱ABCD-A1B1C1D1中,四个侧面都是矩形.
初步应用
证明:由四边形BB1C1C是矩形,得CC1⊥BC.
同理可得CC1⊥CD.
又BC∩CD=C,CD 平面ABCD,因此CC1⊥平面ABCD.
又CC1 平面BB1C1C,于是平面BB1C1C⊥平面ABCD.
求证:平面BB1C1C⊥平面ABCD.
A
B
C
D
C1
D1
B1
A1
例2 如图所示,在四面体A1-ABC中,A1A⊥平面ABC,AB⊥BC,且AA1=AB.
初步应用
(1)四面体A1-ABC中有几组相互垂直的平面?
(2)求二面角A-A1B-C和A1-BC-A的大小.
A
B
C
A1
解析:(1)四面体A1-ABC中有3组互相垂直的平面.
因为A1A⊥平面ABC,A1A 平面A1AC,A1A 平面A1AB,
所以平面ABC⊥平面A1AC,平面ABC⊥平面A1AB.
因为A1A⊥平面ABC,所以A1A⊥BC,
又因为AB⊥BC,AB∩A1A=A,且AB,A1A 平面A1AB,
所以BC⊥平面A1AB,又因为BC 平面A1BC,故平面A1AB⊥平面A1BC.
例2 如图所示,在四面体A1-ABC中,A1A⊥平面ABC,AB⊥BC,且AA1=AB.
初步应用
(1)四面体A1-ABC中有几组相互垂直的平面?
(2)求二面角A-A1B-C和A1-BC-A的大小.
A
B
C
A1
解析:(2)由(1)知二面角A-A1B-C等于90°.
又AB⊥BC,所以∠A1AB即为二面角A1-BC-A的平面角.
因为BC⊥平面A1AB,A1B 平面A1AB,所以BC⊥A1B,
因为又A1A⊥AB,且AA1=AB,所以∠A1AB=45°,即平面A1-BC-A的二面角为45°.
课堂练习
练习:教科书第230页练习1,2,3.
归纳小结
(1)证明平面与平面垂直的方法是什么?
(2)空间中线、面的垂直关系是如何转化的?
问题11 本节课我们学面与平面垂直的判定定理及其应用,请你通过下列问题,归
纳所学知识.
(1)证明平面与平面垂直的方法:
①利用定义:证明二面角的平面角为直角;
②利用面面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直.
(2)转化关系如下:
作业布置
作业:教科书第235页练习1,2,3,4.
1
目标检测
B
在正方体ABCD-A1B1C1D1中,与AD1垂直的平面是( )
A.平面DD1C1C
B.平面A1DB1
C.平面A1B1C1D1
D.平面A1DB
解析: ∵AD1⊥A1D,AD1⊥A1B1,又A1D∩A1B1=A1,
∴AD1⊥平面A1DB1.
故选:B.
2
目标检测
C
在棱长都相等的四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,则下面四个结论中不成立的是( )
A.BC∥平面PDF
C.平面PDF⊥平面ABC
B.DF⊥平面PAE
D.平面PAE⊥平面ABC
解析:可画出对应图形,如图所示,则BC∥DF,
由AE⊥BC,PE⊥BC,BC∥DF,知DF⊥AE,DF⊥PE,
又DF 平面ABC,
故选:C.
又DF 平面PDF,故A成立;
∴DF⊥平面PAE,故B成立;
∴平面ABC⊥平面PAE,故D成立.
3
目标检测
面面垂直的判定定理
如图所示,检查工件的相邻两个面是否垂直时,只要用曲尺的一边紧靠在工件的一个面上,另一边在工件的另一个面上转动,观察尺边是否和这个面密合就可以
了,其原理是利用了__________________________.
解析:如图所示,
因为OA⊥OB,OA⊥OC,OB β,OC β,且OB∩OC=O,
根据线面垂直的判定定理,
可得OA⊥β,又OA α,
根据面面垂直的判定定理,可得α⊥β.
4
目标检测
如图,在三棱台DEF-ABC中,AB=2DE,点G,H分别为AC,BC的中点.
(1)求证:BD∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.
证明:(1)因为DEF-ABC是三棱台,且AB=2DE,
因为点G,H分别是AC,BC的中点,
因为AB 平面FGH,GH 平面FGH,
因为EF∥BH且EF=BH,
所以AB∥平面FGH.
所以四边形BHFE是平行四边形,
因为BE 平面FGH,HF 平面FGH,
所以BC=2EF,AC=2DF.
所以GH∥AB.
所以BE∥平面FGH;
所以BE∥HF.
4
目标检测
如图,在三棱台DEF-ABC中,AB=2DE,点G,H分别为AC,BC的中点.
(1)求证:BD∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.
又因为AB∩BE=B,
因为BD 平面ABE,
(2)因为AB=2DE,
因为H是BC的中点,
所以BC=2EF,
又HC∥EF,
所以平面ABE∥平面FGH,
所以BD∥平面FGH.
所以四边形HCFE是平行四边形,
所以HC= BC=EF,
所以HE∥CF.
4
目标检测
如图,在三棱台DEF-ABC中,AB=2DE,点G,H分别为AC,BC的中点.
(1)求证:BD∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.
因为CF⊥BC,
因为GH∥AB,AB⊥BC,
因为GH∩HE=H,
又BC 平面BCD,
所以BC⊥平面EGH.
所以平面BCD⊥平面EGH.
所以HE⊥BC.
所以GH⊥BC.
6.5 垂直关系
第4课时
导入新课
问题1 在过程建设中,建筑工人用一端系有铅锤的线来检查墙面与地面是否垂直,即若紧贴墙面的铅垂的线垂直地面,则确定墙面与地面垂直,否则不垂直,“紧贴墙面的线”这句话的实质意义是什么?
此线在墙所在的平面内,即平面过另一平面的垂线,则两平面垂直.
新知探究
垂直.
问题3 若要判断两平面是否垂直,根据问题2能否得出一个方法?
可以,
只需在一平面内找一直线垂直于另一平面即可.
问题2 当直线与平面垂直时,过此直线可作无数个平面,那么这些平面与已知平面有何关系?
新知探究
问题4 你能语言和符号表示平面与平面垂直的判定定理吗?
如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直.
简记: α⊥β.
α
β
m
A
O
新知探究
问题5 过已知平面的垂线,有几个平面和已知平面垂直?
过已知平面的垂线,和已知平面垂直的平面有无数个.
α
β
m
A
O
γ
例1 如图所示,在四棱柱ABCD-A1B1C1D1中,四个侧面都是矩形.
初步应用
证明:由四边形BB1C1C是矩形,得CC1⊥BC.
同理可得CC1⊥CD.
又BC∩CD=C,CD 平面ABCD,因此CC1⊥平面ABCD.
又CC1 平面BB1C1C,于是平面BB1C1C⊥平面ABCD.
求证:平面BB1C1C⊥平面ABCD.
A
B
C
D
C1
D1
B1
A1
例2 如图所示,在四面体A1-ABC中,A1A⊥平面ABC,AB⊥BC,且AA1=AB.
初步应用
(1)四面体A1-ABC中有几组相互垂直的平面?
(2)求二面角A-A1B-C和A1-BC-A的大小.
A
B
C
A1
解析:(1)四面体A1-ABC中有3组互相垂直的平面.
因为A1A⊥平面ABC,A1A 平面A1AC,A1A 平面A1AB,
所以平面ABC⊥平面A1AC,平面ABC⊥平面A1AB.
因为A1A⊥平面ABC,所以A1A⊥BC,
又因为AB⊥BC,AB∩A1A=A,且AB,A1A 平面A1AB,
所以BC⊥平面A1AB,又因为BC 平面A1BC,故平面A1AB⊥平面A1BC.
例2 如图所示,在四面体A1-ABC中,A1A⊥平面ABC,AB⊥BC,且AA1=AB.
初步应用
(1)四面体A1-ABC中有几组相互垂直的平面?
(2)求二面角A-A1B-C和A1-BC-A的大小.
A
B
C
A1
解析:(2)由(1)知二面角A-A1B-C等于90°.
又AB⊥BC,所以∠A1AB即为二面角A1-BC-A的平面角.
因为BC⊥平面A1AB,A1B 平面A1AB,所以BC⊥A1B,
因为又A1A⊥AB,且AA1=AB,所以∠A1AB=45°,即平面A1-BC-A的二面角为45°.
课堂练习
练习:教科书第230页练习1,2,3.
归纳小结
(1)证明平面与平面垂直的方法是什么?
(2)空间中线、面的垂直关系是如何转化的?
问题11 本节课我们学面与平面垂直的判定定理及其应用,请你通过下列问题,归
纳所学知识.
(1)证明平面与平面垂直的方法:
①利用定义:证明二面角的平面角为直角;
②利用面面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直.
(2)转化关系如下:
作业布置
作业:教科书第235页练习1,2,3,4.
1
目标检测
B
在正方体ABCD-A1B1C1D1中,与AD1垂直的平面是( )
A.平面DD1C1C
B.平面A1DB1
C.平面A1B1C1D1
D.平面A1DB
解析: ∵AD1⊥A1D,AD1⊥A1B1,又A1D∩A1B1=A1,
∴AD1⊥平面A1DB1.
故选:B.
2
目标检测
C
在棱长都相等的四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,则下面四个结论中不成立的是( )
A.BC∥平面PDF
C.平面PDF⊥平面ABC
B.DF⊥平面PAE
D.平面PAE⊥平面ABC
解析:可画出对应图形,如图所示,则BC∥DF,
由AE⊥BC,PE⊥BC,BC∥DF,知DF⊥AE,DF⊥PE,
又DF 平面ABC,
故选:C.
又DF 平面PDF,故A成立;
∴DF⊥平面PAE,故B成立;
∴平面ABC⊥平面PAE,故D成立.
3
目标检测
面面垂直的判定定理
如图所示,检查工件的相邻两个面是否垂直时,只要用曲尺的一边紧靠在工件的一个面上,另一边在工件的另一个面上转动,观察尺边是否和这个面密合就可以
了,其原理是利用了__________________________.
解析:如图所示,
因为OA⊥OB,OA⊥OC,OB β,OC β,且OB∩OC=O,
根据线面垂直的判定定理,
可得OA⊥β,又OA α,
根据面面垂直的判定定理,可得α⊥β.
4
目标检测
如图,在三棱台DEF-ABC中,AB=2DE,点G,H分别为AC,BC的中点.
(1)求证:BD∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.
证明:(1)因为DEF-ABC是三棱台,且AB=2DE,
因为点G,H分别是AC,BC的中点,
因为AB 平面FGH,GH 平面FGH,
因为EF∥BH且EF=BH,
所以AB∥平面FGH.
所以四边形BHFE是平行四边形,
因为BE 平面FGH,HF 平面FGH,
所以BC=2EF,AC=2DF.
所以GH∥AB.
所以BE∥平面FGH;
所以BE∥HF.
4
目标检测
如图,在三棱台DEF-ABC中,AB=2DE,点G,H分别为AC,BC的中点.
(1)求证:BD∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.
又因为AB∩BE=B,
因为BD 平面ABE,
(2)因为AB=2DE,
因为H是BC的中点,
所以BC=2EF,
又HC∥EF,
所以平面ABE∥平面FGH,
所以BD∥平面FGH.
所以四边形HCFE是平行四边形,
所以HC= BC=EF,
所以HE∥CF.
4
目标检测
如图,在三棱台DEF-ABC中,AB=2DE,点G,H分别为AC,BC的中点.
(1)求证:BD∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.
因为CF⊥BC,
因为GH∥AB,AB⊥BC,
因为GH∩HE=H,
又BC 平面BCD,
所以BC⊥平面EGH.
所以平面BCD⊥平面EGH.
所以HE⊥BC.
所以GH⊥BC.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
