8.1.基本立体图形(棱柱、棱锥、棱台)的结构特征 课件(共30张PPT)
文档属性
| 名称 | 8.1.基本立体图形(棱柱、棱锥、棱台)的结构特征 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 617.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 22:13:37 | ||
图片预览








文档简介
(共30张PPT)
第八章 立体几何
8.1 基本立体图形
授课人:
时间:
8.1 基本立体图形
8.1.1 棱柱、棱锥、棱台的结构特征
在平面几何中,我们认识了三角形,正方形,矩形,菱形,梯形,圆,扇形等平面图形.但我们知道在我们周围存在着各种各样的物体,它们都占据着空间的一部分.如果我们只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些抽象出来的空间图形就叫做空间几何体.那么对空间中各种各样的几何体,我们如何认识它们的结构特征?对空间中不同形状、大小的几何体我们如何理解它们的联系和区别?
【情境导入】
【课前预习】
阅读课本97-100页,思考并完成以下问题1、什么是空间几何体?什么是多面体与旋转体?2、多面体包含哪些图形?这些图形是怎样定义的?又有什么结构特点?
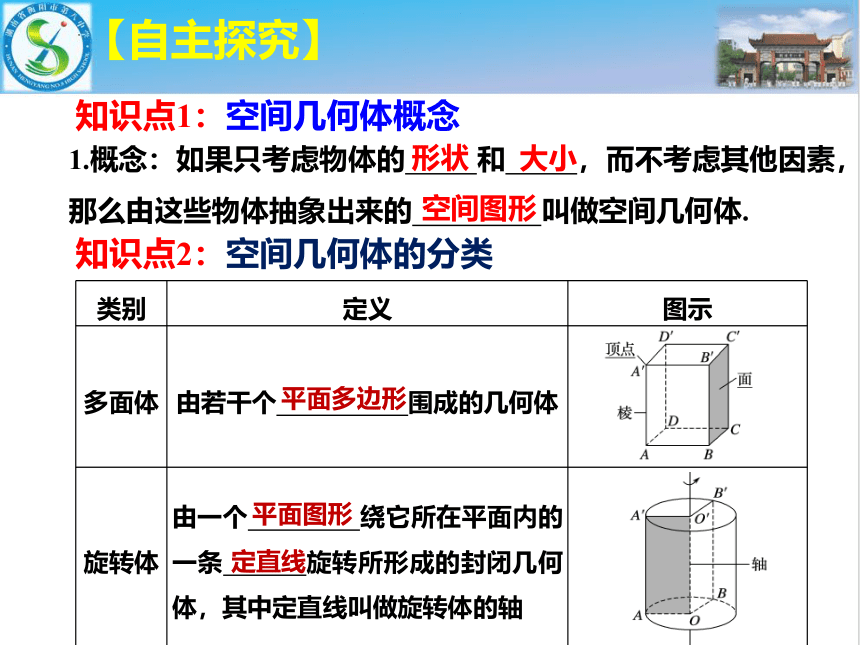
1.概念:如果只考虑物体的 和 ,而不考虑其他因素,那么由这些物体抽象出来的 叫做空间几何体.
空间图形
形状
大小
知识点1:空间几何体概念
【自主探究】
类别 定义 图示
多面体 由若干个 围成的几何体
旋转体 由一个 绕它所在平面内的一条 旋转所形成的封闭几何体,其中定直线叫做旋转体的轴
知识点2:空间几何体的分类
平面多边形
定直线
平面图形
多面体 定义 图形及表示 相关概念 分类
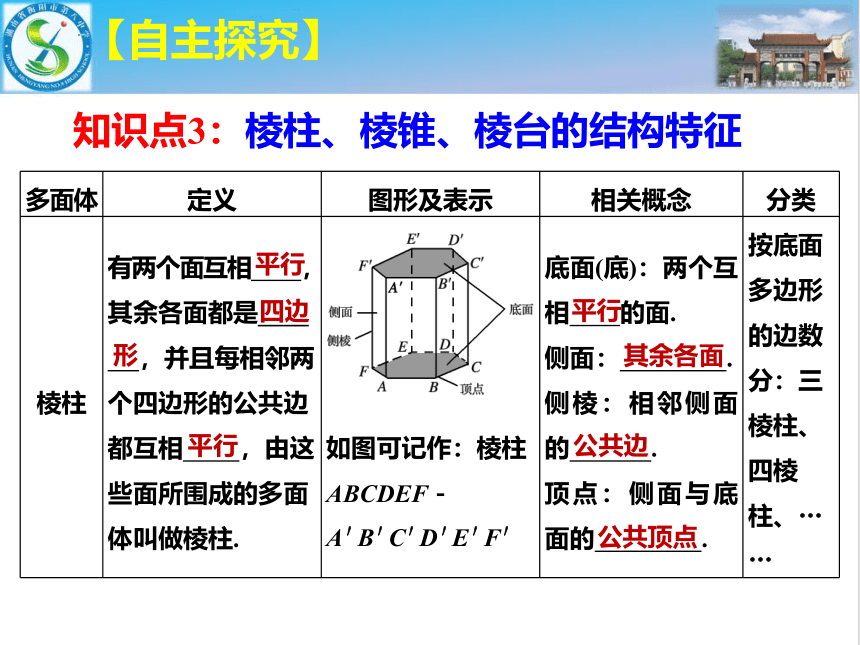
棱柱 有两个面互相 ,其余各面都是____ ,并且每相邻两个四边形的公共边都互相 ,由这些面所围成的多面体叫做棱柱. 如图可记作:棱柱ABCDEF-A′B′C′D′E′F′ 底面(底):两个互相 的面. 侧面: . 侧棱:相邻侧面的 . 顶点:侧面与底面的 . 按底面多边形的边数分:三棱柱、四棱柱、……
平行
公共顶点
平行
四边
形
平行
其余各面
公共边
知识点3:棱柱、棱锥、棱台的结构特征
【自主探究】
直棱柱:侧棱垂直于底面的棱柱
【合作探究】
斜棱柱:侧棱不垂直于底面的棱柱
正棱柱:底面是正多边形的直棱柱
平行六面体:底面是平行四边形的四棱柱
答案
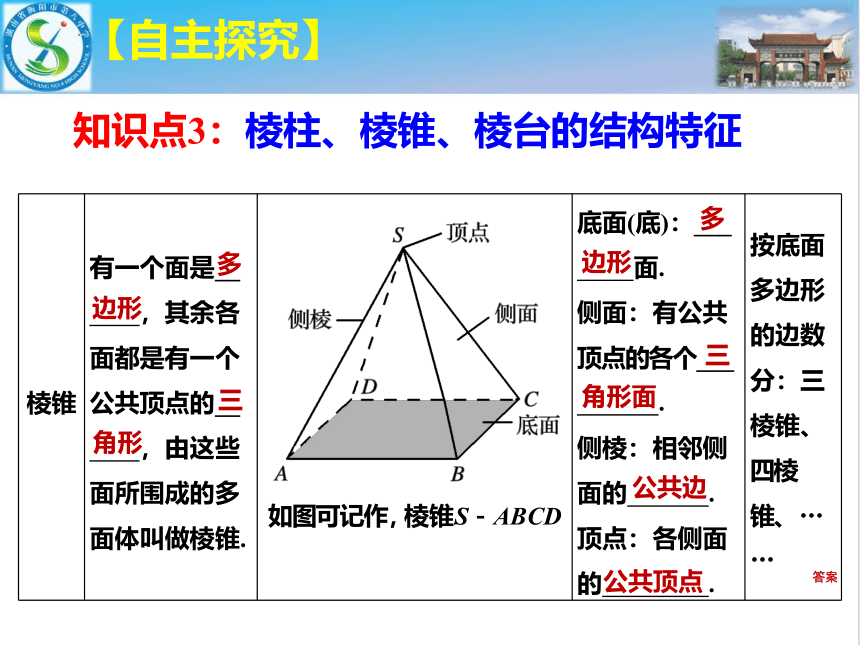
棱锥 有一个面是__ ,其余各面都是有一个公共顶点的__ ,由这些面所围成的多面体叫做棱锥. 如图可记作,棱锥S-ABCD 底面(底):___ 面. 侧面:有公共顶点的各个___ . 侧棱:相邻侧面的 . 顶点:各侧面的 . 按底面多边形的边数分:三棱锥、四棱锥、……
角形
公共顶点
多
边形
三
多
边形
三
角形面
公共边
知识点3:棱柱、棱锥、棱台的结构特征
【自主探究】
【合作探究】
正棱锥:底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥
答案
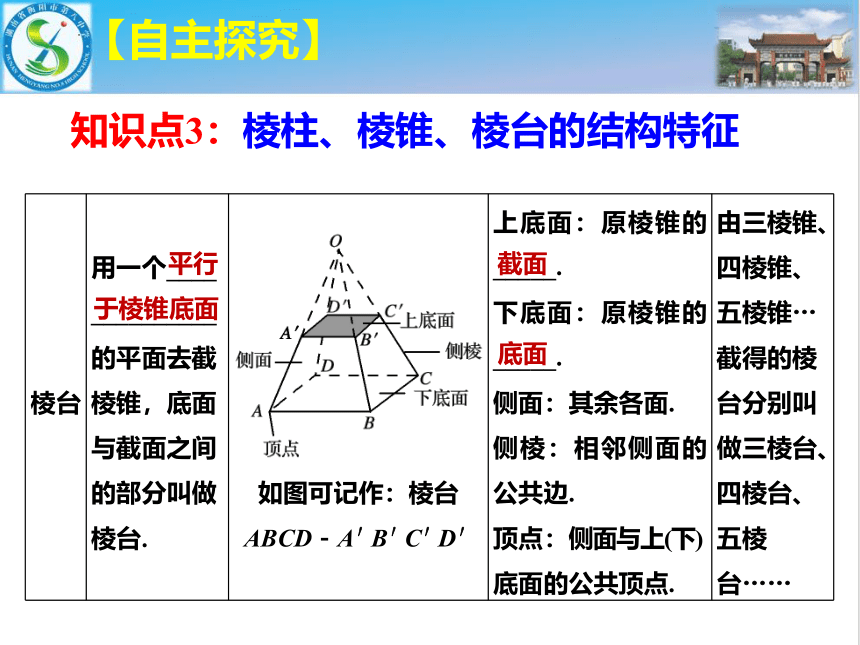
棱台 用一个____ __________ 的平面去截棱锥,底面与截面之间的部分叫做棱台. 如图可记作:棱台ABCD-A′B′C′D′ 上底面:原棱锥的_____. 下底面:原棱锥的_____. 侧面:其余各面. 侧棱:相邻侧面的公共边. 顶点:侧面与上(下) 底面的公共顶点. 由三棱锥、四棱锥、五棱锥…截得的棱台分别叫做三棱台、四棱台、五棱台……
于棱锥底面
底面
平行
截面
知识点3:棱柱、棱锥、棱台的结构特征
【自主探究】
【例1】下列关于棱柱的说法:
(1)所有的面都是平行四边形;(2)每一个面都不会是三角形;
(3)两底面平行,并且各侧棱也平行;(4)被平面截成的两部分 可以都是棱柱.其中正确说法的序号是________.
【合作探究】
【探究一】 棱柱的结构特征
(3)(4)
[解析] (1)错误,棱柱的底面不一定是平行四边形;(2)错误,棱柱的底面可以是三角形;(3)正确,由棱柱的定义易知;(4)正确,棱柱可以被平行于底面的平面截成两个棱柱.所以说法正确的序号是(3)(4).
反思感悟
棱柱的结构特征:
1有两个面互相平行且全等;
2其余各面是平行四边形;
3相邻侧面的公共边都互相平行.
求解时,首先看是否有两个平行的面作为底面,
再看是否满足其他特征
【跟踪训练1】如图,已知长方体ABCD A1B1C1D,
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?(2)用平面BCFE把这个长方体分成两部分后,各部分形成的几何体还是棱柱吗?如果是,是几棱柱?如果不是,请说明理由.
(2)截面BCFE上方的部分是棱柱,且是三棱柱BEB1 CFC1,其中△BEB1和△CFC1是底面.截面BCFE下方的部分也是棱柱,且是四棱柱ABEA1 DCFD1,其中四边形ABEA1和四边形DCFD1是底面.
解:(1)是棱柱,并且是四棱柱.因为以长方体相对的两个面作为底面,则底面都是四边形,其余各面都是矩形,矩形当然是平行四边形,并且几何体的四条侧棱互相平行.
【合作探究】
. .
【例2】(1)下列关于棱锥、棱台的说法:①棱台的侧面一定不会是平行四边形;
②棱锥的侧面只能是三角形;③由四个面围成的封闭图形只能是三棱锥;
④棱锥被平面截成的两部分不可能都是棱锥.其中正确说法的序号是________.
(2)如图,在三棱台A′B′C′ ABC中,截去三棱锥A′ ABC,则剩余部分是( )
A.三棱锥 B.四棱锥 C.三棱柱 D.三棱台
①②③
B
【合作探究】
【探究二】 棱锥、棱台的结构特征
【解】(1)①正确,棱台的侧面都是梯形.②正确,由棱锥的定义知棱锥的侧面只能是三角形.③正确,由四个面围成的封闭图形只能是三棱锥.④错误,如图所示,四棱锥被平面截成的两部分都是棱锥.(2)由题图知,在三棱台A′B′C′ ABC中,截去三棱锥A′ ABC,剩下的部分如图所示,故剩余部分是四棱锥A′ BB′C′C.
归纳总结:判断棱锥、棱台形状的两个方法(1)举反例法:结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确.(2)直接法:
棱锥 棱台
定底面 只有一个面是多边形,此面即为底面 两个互相平行的面,即为底面
看侧棱 相交于一点 延长后相交于一点
反思感悟
【跟踪训练2】(1)下列特征不是棱台必须具有的是( ) A.两底面平行 B.侧面都是梯形
C.侧棱长都相等 D.侧棱延长后相交于一点
【答案】C解析:用平行于棱锥底面的平面截棱锥,截面和底面之间的部分叫做棱台,A,B,D正确,选C.
【合作探究】
【探究二】 棱锥、棱台的结构特征
【例3】画出如图所示的几何体的表面展开图.
解 表面展开图如图所示:
【合作探究】
【探究三】 空间几何体的表面展开图
【跟踪训练3】如图是三个几何体的侧面展开图,请问各是什么几何体?
解:如图:
所以(1)为五棱柱;(2)为五棱锥;(3)为三棱台.
【例4】如图所示,在侧棱长为2 的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=40°,过点A作截面AEF分别交VB,VC于点E,F,求截面△AEF周长的最小值.
解 将三棱锥V-ABC沿侧棱VA剪开,将其侧面展开图平铺在一个平面上,如图所示,则△AEF的周长=AE+EF+FA1.因为AE+EF+FA1≥AA1,
所以线段AA1(即A,E,F,A1四点共线时)的长即为所求△AEF周长的最小值.作VD⊥AA1,垂足为点D.
由VA=VA1,知D为AA1的中点.由已知∠AVB=∠BVC
=∠CVA1=40°,得∠AVD=60°.
即AA1=2AD=6.所以截面△AEF周长的最小值是6.
【拓展延伸】
【探究四】 截面周长最小问题
解题技巧(多面体展开图的解题策略)
(1)由展开图复原几何体:若是给出多面体的平面展开图,来判断是由哪一个多面体展开的,则可把上述过程逆推.同一个几何体的平面展开图可能是不一样的,也就是说,一个多面体可有多个平面展开图.
(2)求几何体表面上两点间的距离的方法:求从几何体的表面上一点,沿几何体表面运动到另一点,所走过的最短距离,常将几何体沿某条棱剪开,使两点展在一个平面上,转化为求平面上两点间的最短距离问题.
反思感悟
【跟踪训练4】长方体ABCD-A1B1C1D1中, AB=4,BC=3,BB1=5,一只蚂蚁从点A出发沿表面爬行到点C1,求蚂蚁爬行的最短路线.
【拓展延伸】
【探究四】 截面周长最小问题
解析答案
1.下列命题中,真命题是( )
A.顶点在底面上的投影到底面各顶点的距离相等的三棱锥是正三棱锥
B.底面是正三角形,各侧面是等腰三角形的三棱锥是正三棱锥
C.顶点在底面上的投影为底面三角形的垂心的三棱锥是正三棱锥
D.底面是正三角形,并且侧棱都相等的三棱锥是正三棱锥
【随堂训练】
D
解析 对于选项A,到三角形各顶点距离相等的点为三角形外心,该三角形不一定为正三角形,故该命题是假命题;
对于选项B,如图所示,△ABC为正三角形,若PA=PB
=AB=BC=AC≠PC,△PAB,△PBC,△PAC都是等
腰三角形,但它不是正三棱锥,故该命题是假命题;
对于选项C,顶点在底面上的投影为底面三角形的垂心,底面为任意三角形皆可,故该命题是假命题;
对于选项D,顶点在底面上的正投影是底面三角形的外心,又因为底面三角形为正三角形,所以外心即为中心,故该命题是真命题.
答案 D
解析答案
2.下列三个命题:
①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;
②两个底面平行且相似,其余各面都是菱形的多面体是棱台;
③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.
其中,正确的有( )
A.0个 B.1个 C.2个 D.3个
A
解析 ①中的平面不一定平行于底面,故①错;
②中侧面是菱形,所以侧棱互相平行,延长后无交点,故②错;
③用反例验证(如图),故③错.
1
2
3
4
5
解析答案
1
2
3
4
5
3.下列几何体中,________是棱柱,____是棱锥,____是棱台(仅填相应序号).
解析 结合棱柱、棱锥和棱台的定义可知①③④是棱柱,⑥是棱锥,⑤是棱台.
①③④
⑥
⑤
【随堂训练】
1
2
3
4
5
解析答案
4.如图,将装有水的长方体水槽固定底面一边后将水槽倾斜一个小角度,则倾斜后水槽中的水形成的几何体的形状是 .
解析 由于倾斜角度较小,所以倾斜后水槽中水形成的几何体的形状应为四棱柱.
四棱柱
【随堂训练】
【课堂小结】
1.空间几何体的定义
2.空间几何体的分类
(1)多面体
(2)旋转体
3.棱柱、棱锥、棱台的结构特征
4.棱柱、棱锥、棱台的关系
在运动变化的观点下,棱柱、棱锥、棱台之间的关系可以用下图表示出来(以三棱柱、三棱锥、三棱台为例).
【课堂小结】
【作业布置】
【作业】
横格本:教科书P101,T1、T2、T3.
必刷题:P55
感谢聆听
第八章 立体几何
8.1 基本立体图形
授课人:
时间:
8.1 基本立体图形
8.1.1 棱柱、棱锥、棱台的结构特征
在平面几何中,我们认识了三角形,正方形,矩形,菱形,梯形,圆,扇形等平面图形.但我们知道在我们周围存在着各种各样的物体,它们都占据着空间的一部分.如果我们只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些抽象出来的空间图形就叫做空间几何体.那么对空间中各种各样的几何体,我们如何认识它们的结构特征?对空间中不同形状、大小的几何体我们如何理解它们的联系和区别?
【情境导入】
【课前预习】
阅读课本97-100页,思考并完成以下问题1、什么是空间几何体?什么是多面体与旋转体?2、多面体包含哪些图形?这些图形是怎样定义的?又有什么结构特点?
1.概念:如果只考虑物体的 和 ,而不考虑其他因素,那么由这些物体抽象出来的 叫做空间几何体.
空间图形
形状
大小
知识点1:空间几何体概念
【自主探究】
类别 定义 图示
多面体 由若干个 围成的几何体
旋转体 由一个 绕它所在平面内的一条 旋转所形成的封闭几何体,其中定直线叫做旋转体的轴
知识点2:空间几何体的分类
平面多边形
定直线
平面图形
多面体 定义 图形及表示 相关概念 分类
棱柱 有两个面互相 ,其余各面都是____ ,并且每相邻两个四边形的公共边都互相 ,由这些面所围成的多面体叫做棱柱. 如图可记作:棱柱ABCDEF-A′B′C′D′E′F′ 底面(底):两个互相 的面. 侧面: . 侧棱:相邻侧面的 . 顶点:侧面与底面的 . 按底面多边形的边数分:三棱柱、四棱柱、……
平行
公共顶点
平行
四边
形
平行
其余各面
公共边
知识点3:棱柱、棱锥、棱台的结构特征
【自主探究】
直棱柱:侧棱垂直于底面的棱柱
【合作探究】
斜棱柱:侧棱不垂直于底面的棱柱
正棱柱:底面是正多边形的直棱柱
平行六面体:底面是平行四边形的四棱柱
答案
棱锥 有一个面是__ ,其余各面都是有一个公共顶点的__ ,由这些面所围成的多面体叫做棱锥. 如图可记作,棱锥S-ABCD 底面(底):___ 面. 侧面:有公共顶点的各个___ . 侧棱:相邻侧面的 . 顶点:各侧面的 . 按底面多边形的边数分:三棱锥、四棱锥、……
角形
公共顶点
多
边形
三
多
边形
三
角形面
公共边
知识点3:棱柱、棱锥、棱台的结构特征
【自主探究】
【合作探究】
正棱锥:底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥
答案
棱台 用一个____ __________ 的平面去截棱锥,底面与截面之间的部分叫做棱台. 如图可记作:棱台ABCD-A′B′C′D′ 上底面:原棱锥的_____. 下底面:原棱锥的_____. 侧面:其余各面. 侧棱:相邻侧面的公共边. 顶点:侧面与上(下) 底面的公共顶点. 由三棱锥、四棱锥、五棱锥…截得的棱台分别叫做三棱台、四棱台、五棱台……
于棱锥底面
底面
平行
截面
知识点3:棱柱、棱锥、棱台的结构特征
【自主探究】
【例1】下列关于棱柱的说法:
(1)所有的面都是平行四边形;(2)每一个面都不会是三角形;
(3)两底面平行,并且各侧棱也平行;(4)被平面截成的两部分 可以都是棱柱.其中正确说法的序号是________.
【合作探究】
【探究一】 棱柱的结构特征
(3)(4)
[解析] (1)错误,棱柱的底面不一定是平行四边形;(2)错误,棱柱的底面可以是三角形;(3)正确,由棱柱的定义易知;(4)正确,棱柱可以被平行于底面的平面截成两个棱柱.所以说法正确的序号是(3)(4).
反思感悟
棱柱的结构特征:
1有两个面互相平行且全等;
2其余各面是平行四边形;
3相邻侧面的公共边都互相平行.
求解时,首先看是否有两个平行的面作为底面,
再看是否满足其他特征
【跟踪训练1】如图,已知长方体ABCD A1B1C1D,
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?(2)用平面BCFE把这个长方体分成两部分后,各部分形成的几何体还是棱柱吗?如果是,是几棱柱?如果不是,请说明理由.
(2)截面BCFE上方的部分是棱柱,且是三棱柱BEB1 CFC1,其中△BEB1和△CFC1是底面.截面BCFE下方的部分也是棱柱,且是四棱柱ABEA1 DCFD1,其中四边形ABEA1和四边形DCFD1是底面.
解:(1)是棱柱,并且是四棱柱.因为以长方体相对的两个面作为底面,则底面都是四边形,其余各面都是矩形,矩形当然是平行四边形,并且几何体的四条侧棱互相平行.
【合作探究】
. .
【例2】(1)下列关于棱锥、棱台的说法:①棱台的侧面一定不会是平行四边形;
②棱锥的侧面只能是三角形;③由四个面围成的封闭图形只能是三棱锥;
④棱锥被平面截成的两部分不可能都是棱锥.其中正确说法的序号是________.
(2)如图,在三棱台A′B′C′ ABC中,截去三棱锥A′ ABC,则剩余部分是( )
A.三棱锥 B.四棱锥 C.三棱柱 D.三棱台
①②③
B
【合作探究】
【探究二】 棱锥、棱台的结构特征
【解】(1)①正确,棱台的侧面都是梯形.②正确,由棱锥的定义知棱锥的侧面只能是三角形.③正确,由四个面围成的封闭图形只能是三棱锥.④错误,如图所示,四棱锥被平面截成的两部分都是棱锥.(2)由题图知,在三棱台A′B′C′ ABC中,截去三棱锥A′ ABC,剩下的部分如图所示,故剩余部分是四棱锥A′ BB′C′C.
归纳总结:判断棱锥、棱台形状的两个方法(1)举反例法:结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确.(2)直接法:
棱锥 棱台
定底面 只有一个面是多边形,此面即为底面 两个互相平行的面,即为底面
看侧棱 相交于一点 延长后相交于一点
反思感悟
【跟踪训练2】(1)下列特征不是棱台必须具有的是( ) A.两底面平行 B.侧面都是梯形
C.侧棱长都相等 D.侧棱延长后相交于一点
【答案】C解析:用平行于棱锥底面的平面截棱锥,截面和底面之间的部分叫做棱台,A,B,D正确,选C.
【合作探究】
【探究二】 棱锥、棱台的结构特征
【例3】画出如图所示的几何体的表面展开图.
解 表面展开图如图所示:
【合作探究】
【探究三】 空间几何体的表面展开图
【跟踪训练3】如图是三个几何体的侧面展开图,请问各是什么几何体?
解:如图:
所以(1)为五棱柱;(2)为五棱锥;(3)为三棱台.
【例4】如图所示,在侧棱长为2 的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=40°,过点A作截面AEF分别交VB,VC于点E,F,求截面△AEF周长的最小值.
解 将三棱锥V-ABC沿侧棱VA剪开,将其侧面展开图平铺在一个平面上,如图所示,则△AEF的周长=AE+EF+FA1.因为AE+EF+FA1≥AA1,
所以线段AA1(即A,E,F,A1四点共线时)的长即为所求△AEF周长的最小值.作VD⊥AA1,垂足为点D.
由VA=VA1,知D为AA1的中点.由已知∠AVB=∠BVC
=∠CVA1=40°,得∠AVD=60°.
即AA1=2AD=6.所以截面△AEF周长的最小值是6.
【拓展延伸】
【探究四】 截面周长最小问题
解题技巧(多面体展开图的解题策略)
(1)由展开图复原几何体:若是给出多面体的平面展开图,来判断是由哪一个多面体展开的,则可把上述过程逆推.同一个几何体的平面展开图可能是不一样的,也就是说,一个多面体可有多个平面展开图.
(2)求几何体表面上两点间的距离的方法:求从几何体的表面上一点,沿几何体表面运动到另一点,所走过的最短距离,常将几何体沿某条棱剪开,使两点展在一个平面上,转化为求平面上两点间的最短距离问题.
反思感悟
【跟踪训练4】长方体ABCD-A1B1C1D1中, AB=4,BC=3,BB1=5,一只蚂蚁从点A出发沿表面爬行到点C1,求蚂蚁爬行的最短路线.
【拓展延伸】
【探究四】 截面周长最小问题
解析答案
1.下列命题中,真命题是( )
A.顶点在底面上的投影到底面各顶点的距离相等的三棱锥是正三棱锥
B.底面是正三角形,各侧面是等腰三角形的三棱锥是正三棱锥
C.顶点在底面上的投影为底面三角形的垂心的三棱锥是正三棱锥
D.底面是正三角形,并且侧棱都相等的三棱锥是正三棱锥
【随堂训练】
D
解析 对于选项A,到三角形各顶点距离相等的点为三角形外心,该三角形不一定为正三角形,故该命题是假命题;
对于选项B,如图所示,△ABC为正三角形,若PA=PB
=AB=BC=AC≠PC,△PAB,△PBC,△PAC都是等
腰三角形,但它不是正三棱锥,故该命题是假命题;
对于选项C,顶点在底面上的投影为底面三角形的垂心,底面为任意三角形皆可,故该命题是假命题;
对于选项D,顶点在底面上的正投影是底面三角形的外心,又因为底面三角形为正三角形,所以外心即为中心,故该命题是真命题.
答案 D
解析答案
2.下列三个命题:
①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;
②两个底面平行且相似,其余各面都是菱形的多面体是棱台;
③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.
其中,正确的有( )
A.0个 B.1个 C.2个 D.3个
A
解析 ①中的平面不一定平行于底面,故①错;
②中侧面是菱形,所以侧棱互相平行,延长后无交点,故②错;
③用反例验证(如图),故③错.
1
2
3
4
5
解析答案
1
2
3
4
5
3.下列几何体中,________是棱柱,____是棱锥,____是棱台(仅填相应序号).
解析 结合棱柱、棱锥和棱台的定义可知①③④是棱柱,⑥是棱锥,⑤是棱台.
①③④
⑥
⑤
【随堂训练】
1
2
3
4
5
解析答案
4.如图,将装有水的长方体水槽固定底面一边后将水槽倾斜一个小角度,则倾斜后水槽中的水形成的几何体的形状是 .
解析 由于倾斜角度较小,所以倾斜后水槽中水形成的几何体的形状应为四棱柱.
四棱柱
【随堂训练】
【课堂小结】
1.空间几何体的定义
2.空间几何体的分类
(1)多面体
(2)旋转体
3.棱柱、棱锥、棱台的结构特征
4.棱柱、棱锥、棱台的关系
在运动变化的观点下,棱柱、棱锥、棱台之间的关系可以用下图表示出来(以三棱柱、三棱锥、三棱台为例).
【课堂小结】
【作业布置】
【作业】
横格本:教科书P101,T1、T2、T3.
必刷题:P55
感谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
