8.2 立体图形的直观图 课件(共26张PPT)
文档属性
| 名称 | 8.2 立体图形的直观图 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 743.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 22:14:05 | ||
图片预览







文档简介
(共26张PPT)
第八章 立体几何初步
授课人:
时间:
8.2 立体图形的直观图
1.把一本书正面放置,其视觉效果是一个矩形;把一本书水平放置,其视觉效果还是一个矩形吗?这涉及水平放置的平面图形的画法问题.
2.对于柱体、锥体、台体及简单的组合体,在平面上应怎样作图才具有强烈的立体感?这涉及空间几何体的直观图的画法问题.
【问题引入】
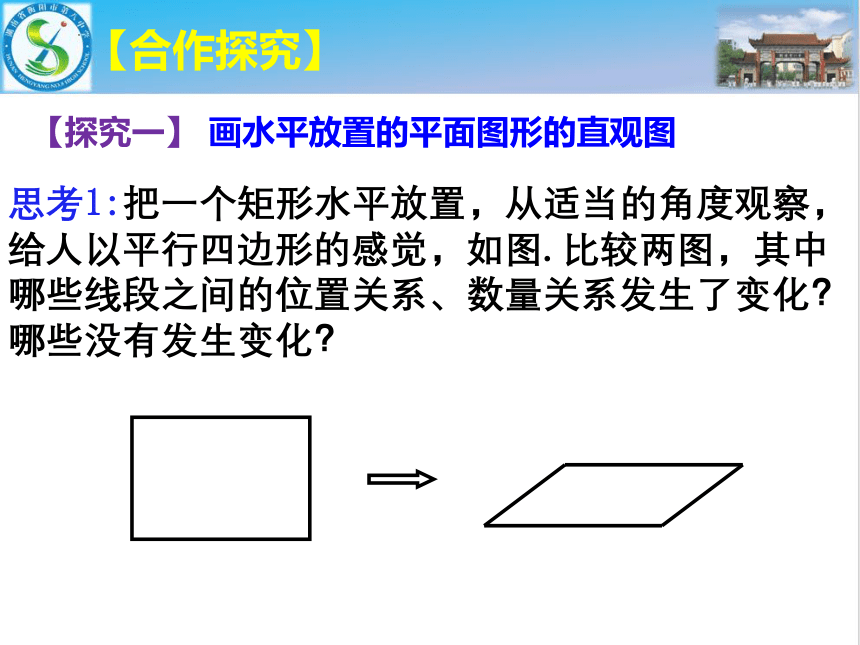
思考1:把一个矩形水平放置,从适当的角度观察,给人以平行四边形的感觉,如图.比较两图,其中哪些线段之间的位置关系、数量关系发生了变化?哪些没有发生变化?
【合作探究】
【探究一】 画水平放置的平面图形的直观图
1.画轴:在已知图形中取互相垂直的x轴和y轴,两轴相交于点O,画直观图时,把它们画成对应的x′轴与y′轴,两轴交于点O′,且使∠x′O′y′= (或 ),它们确定的平面表示 .
2.画线:已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于 或 .
3.取长度:已知图形中平行于x轴的线段,在直观图中保持原长度不变,平行于y轴的线段,长度为原来的一半.
y′轴的线段
45°
135°
水平面
x′轴
知识点1:水平放置的平面图形的直观图画法
画法:用斜二测画法
【合作探究】
斜二测画法的基本步骤和规则:
(1)建坐标系,定水平面;
(3)水平线段等长,竖直线段减半.
(2)与坐标轴平行的线段保持平行;
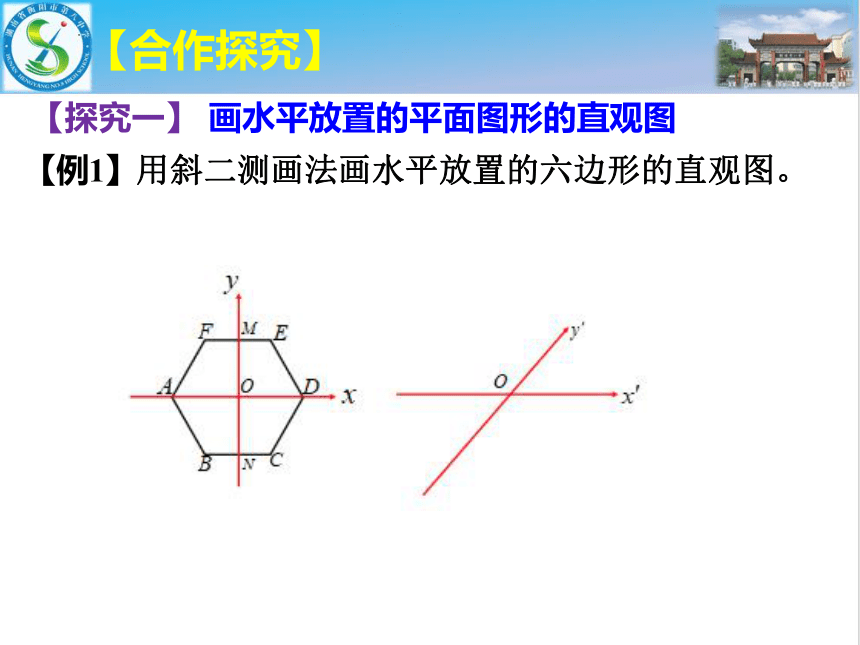
【例1】用斜二测画法画水平放置的六边形的直观图。
【合作探究】
【探究一】 画水平放置的平面图形的直观图
【例1】用斜二测画法画水平放置的六边形的直观图。
【合作探究】
【探究一】 画水平放置的平面图形的直观图
【例1】用斜二测画法画水平放置的六边形的直观图。
【合作探究】
【探究一】 画水平放置的平面图形的直观图
【合作探究】
【探究一】 画水平放置的平面图形的直观图
【例2】如图所示,在梯形ABCD中,AB∥CD,AB=4 cm,CD=2 cm,∠A=30°,AD=3 cm,试画出它的直观图.
解(1)如图①所示,在梯形ABCD中,以边AB所在的直线为x轴,点A为原点,建立平面直角坐标系xOy,如图②所示,画出对应的x′轴,y′轴,使∠x′O′y′=45°.
(2)在图①中,过点D作DE⊥x轴,垂足为E.
【练习1】画边长为1 cm的正三角形的水平放置的直观图.
解:(1)如图①所示,以BC边所在直线为x轴,以BC边上的高线AO所在直线为y轴,再画对应的x′轴与y′轴,两轴相交于点O′,使∠x′O′y′=45°,如图②所示.
(2)在x′轴上截取O′B′=O′C′=0.5 cm,在y′轴上截取 cm,连接A′B′、A′C′,则△A′B′C′即为正三角形ABC的直观图.(3)擦去x′、y′轴得直观图△A′B′C′,如图③所示.
【合作探究】
【探究一】 画水平放置的平面图形的直观图
1.画轴:与平面图形的直观图画法相比多了一个z轴,直观图中与之对应的是 轴.
2.画底面:平面 表示水平平面,平面 ,
和 表示竖直平面.
3.画侧棱:已知图形中平行于z轴(或在z轴上)的线段,在其直观图中_____ 和 都不变.
4.成图:去掉辅助线,将被遮挡的部分改为虚线.
思考 空间几何体的直观图惟一吗?
答:不惟一.作直观图时,由于选轴的不同,画出的直观图也不同.
长度
z′
x′O′y′
y′O′z′
x′O′z′
平行性
知识点2:空间几何体直观图的画法
【合作探究】
【例3】用斜二测画法画长、宽、高分别是4 cm、3 cm、2 cm的长方体ABCD A′B′C′D′的直观图.
【合作探究】
【探究二】 画空间几何体的直观图
解(1)画轴.如图①所示,画x轴、y轴、z轴,三轴相交于点O,使∠xOy=45°,∠xOz=90°.(2)画底面.以点O为中心,在x轴上取线段MN,使MN=4 cm;在y轴上取线段PQ,使PQ= cm,分别过点M和点N作y轴的平行线,过点P和Q作x轴的平行线,设它们的交点分别为A、B、C、D,四边形ABCD就是长方体的底面ABCD.(3)画侧棱.过A、B、C、D各点分别作z轴的平行线,并在这些平行线上分别截取2 cm长的线段AA′、BB′、CC′、DD′.(4)成图.顺次连接A′、B′、C′、D′,并加以整理(擦掉辅助线,将被遮挡的线改为虚线),就得到长方体的直观图(如图②).
【跟踪训练2】一个几何体,它的下面是一个圆柱,上面是一个圆锥,并且圆锥的底面与圆柱的上底面重合,圆柱的底面直径为3 cm,高为4 cm,圆锥的高为3 cm,画出此几何体的直观图.
【合作探究】
【探究二】 画空间几何体的直观图
【例4】如图所示,梯形A1B1C1D1是一平面图形ABCD的直观图.若A1D1∥O′y′,A1B1∥C1D1,A1B1= C1D1=2,A1D1=O′D1=1.求原四边形ABCD的面积.
【合作探究】
【探究二】 由直观图还原成原图
[解]如图,建立平面直角坐标系xOy,在x轴上截取OD=O′D1=1,OC=O′C1=2.
在过点D的y轴的平行线上截取DA=2D1A1=2.在过点A的x轴的平行线上截取AB=A1B1=2.连接BC,即得到了原图形(如图).由作法可知,原四边形ABCD是直角梯形,上、下底长度分别为AB=2,CD=3,直角腰长度为AD=2.所以面积为S=5.
【跟踪训练3】如图,矩形O′A′B′C′是水平放置的一个平面图形用斜二测画法得到的直观图,其中O′A′=6 cm,O′C′=2 cm,则原图形是( )
A.正方形 B.矩形
C.菱形 D.梯形
【答案】C解析:将直观图还原得到平行四边形OABC,如图所示,由题意知O′D′=O′C′=2 cm,OD=2O′D′=4 cm,C′D′=O′C′=2 cm,∴CD=2 cm,OC==6 cm,又OA=O′A′=6 cm,∴OA=OC,∴原图形为菱形.
【合作探究】
【探究三】 由直观图还原成原图
【拓展延伸】
【探究四】 有关直观图与原图的计算问题
【例4】已知用斜二测画法,画得的正方形的直观图面积为 ,则原正方形的面积为________.
【解】如图所示,作出正方形OABC的直观图O′A′B′C′,
作C′D′⊥x′轴于点D′.
【跟踪训练4】已知ΔABC的平面直观图ΔA′B′C′是边长为a的等边三角形,那么ΔABC的面积为( )
【拓展延伸】
【探究四】 有关直观图与原图的计算问题
【解】如图①为直观图,②为实际图形,
C
分析 求直观图的面积的关键是依据斜二测画法,求出相应的直观图的底边和高.
解析 如图①为直观图,②为实际图形,取B′C′所在直线为x′轴,过B′C′中点O′与O′x′成45°的直线为y′轴,过点A′作A′N′∥O′x′.交y′轴于点N′,过点A′作A′M′∥O′y′,交x′轴于点M′,
解析答案
解后反思
则在Rt△A′O′M′中,
答案 C
1
2
3
4
5
1.用斜二测画法画水平放置的平面图形的直观图,对其中的线段说法错误的是( )
A.原来相交的仍相交 B.原来垂直的仍垂直
C.原来平行的仍平行 D.原来共点的仍共点
B
【随堂训练】
2.如图所示为某一平面图形的直观图,则此平面图形可能是( )
C
1
2
3
4
5
3.已知等边三角形ABC的边长为a,那么等边三角形ABC的直观图△A′B′C′的面积为( )
D
4.如图,平行四边形O′P′Q′R′是四边形OPQR的直观图,若O′P′=3,O′R′=1,则原四边形OPQR的周长为_____.
10
5.已知如图所示的直观图△A′O′B′,则其
平面图形的面积为____.
6
【随堂训练】
1
2
3
4
5
解析答案
解析 方法一 建立如图①所示的平面直角坐标系xOy.
1
2
3
4
5
答案 D
1.水平放置平面图形直观图斜二测画法步骤:画轴取轴——取点——连线成图口诀:横不变纵减半,平行性不变2.空间几何体直观图斜二测画法步骤:画轴——画底面——画侧棱——连线成图口诀:横竖不变纵减半,平行性不变3.原图形的面积和直观图面积的关系:
【课时小结】
【作业布置】
【作业】
横格本:教科书P111-112,T1-T7.
必刷题:P60-61.
感谢聆听
第八章 立体几何初步
授课人:
时间:
8.2 立体图形的直观图
1.把一本书正面放置,其视觉效果是一个矩形;把一本书水平放置,其视觉效果还是一个矩形吗?这涉及水平放置的平面图形的画法问题.
2.对于柱体、锥体、台体及简单的组合体,在平面上应怎样作图才具有强烈的立体感?这涉及空间几何体的直观图的画法问题.
【问题引入】
思考1:把一个矩形水平放置,从适当的角度观察,给人以平行四边形的感觉,如图.比较两图,其中哪些线段之间的位置关系、数量关系发生了变化?哪些没有发生变化?
【合作探究】
【探究一】 画水平放置的平面图形的直观图
1.画轴:在已知图形中取互相垂直的x轴和y轴,两轴相交于点O,画直观图时,把它们画成对应的x′轴与y′轴,两轴交于点O′,且使∠x′O′y′= (或 ),它们确定的平面表示 .
2.画线:已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于 或 .
3.取长度:已知图形中平行于x轴的线段,在直观图中保持原长度不变,平行于y轴的线段,长度为原来的一半.
y′轴的线段
45°
135°
水平面
x′轴
知识点1:水平放置的平面图形的直观图画法
画法:用斜二测画法
【合作探究】
斜二测画法的基本步骤和规则:
(1)建坐标系,定水平面;
(3)水平线段等长,竖直线段减半.
(2)与坐标轴平行的线段保持平行;
【例1】用斜二测画法画水平放置的六边形的直观图。
【合作探究】
【探究一】 画水平放置的平面图形的直观图
【例1】用斜二测画法画水平放置的六边形的直观图。
【合作探究】
【探究一】 画水平放置的平面图形的直观图
【例1】用斜二测画法画水平放置的六边形的直观图。
【合作探究】
【探究一】 画水平放置的平面图形的直观图
【合作探究】
【探究一】 画水平放置的平面图形的直观图
【例2】如图所示,在梯形ABCD中,AB∥CD,AB=4 cm,CD=2 cm,∠A=30°,AD=3 cm,试画出它的直观图.
解(1)如图①所示,在梯形ABCD中,以边AB所在的直线为x轴,点A为原点,建立平面直角坐标系xOy,如图②所示,画出对应的x′轴,y′轴,使∠x′O′y′=45°.
(2)在图①中,过点D作DE⊥x轴,垂足为E.
【练习1】画边长为1 cm的正三角形的水平放置的直观图.
解:(1)如图①所示,以BC边所在直线为x轴,以BC边上的高线AO所在直线为y轴,再画对应的x′轴与y′轴,两轴相交于点O′,使∠x′O′y′=45°,如图②所示.
(2)在x′轴上截取O′B′=O′C′=0.5 cm,在y′轴上截取 cm,连接A′B′、A′C′,则△A′B′C′即为正三角形ABC的直观图.(3)擦去x′、y′轴得直观图△A′B′C′,如图③所示.
【合作探究】
【探究一】 画水平放置的平面图形的直观图
1.画轴:与平面图形的直观图画法相比多了一个z轴,直观图中与之对应的是 轴.
2.画底面:平面 表示水平平面,平面 ,
和 表示竖直平面.
3.画侧棱:已知图形中平行于z轴(或在z轴上)的线段,在其直观图中_____ 和 都不变.
4.成图:去掉辅助线,将被遮挡的部分改为虚线.
思考 空间几何体的直观图惟一吗?
答:不惟一.作直观图时,由于选轴的不同,画出的直观图也不同.
长度
z′
x′O′y′
y′O′z′
x′O′z′
平行性
知识点2:空间几何体直观图的画法
【合作探究】
【例3】用斜二测画法画长、宽、高分别是4 cm、3 cm、2 cm的长方体ABCD A′B′C′D′的直观图.
【合作探究】
【探究二】 画空间几何体的直观图
解(1)画轴.如图①所示,画x轴、y轴、z轴,三轴相交于点O,使∠xOy=45°,∠xOz=90°.(2)画底面.以点O为中心,在x轴上取线段MN,使MN=4 cm;在y轴上取线段PQ,使PQ= cm,分别过点M和点N作y轴的平行线,过点P和Q作x轴的平行线,设它们的交点分别为A、B、C、D,四边形ABCD就是长方体的底面ABCD.(3)画侧棱.过A、B、C、D各点分别作z轴的平行线,并在这些平行线上分别截取2 cm长的线段AA′、BB′、CC′、DD′.(4)成图.顺次连接A′、B′、C′、D′,并加以整理(擦掉辅助线,将被遮挡的线改为虚线),就得到长方体的直观图(如图②).
【跟踪训练2】一个几何体,它的下面是一个圆柱,上面是一个圆锥,并且圆锥的底面与圆柱的上底面重合,圆柱的底面直径为3 cm,高为4 cm,圆锥的高为3 cm,画出此几何体的直观图.
【合作探究】
【探究二】 画空间几何体的直观图
【例4】如图所示,梯形A1B1C1D1是一平面图形ABCD的直观图.若A1D1∥O′y′,A1B1∥C1D1,A1B1= C1D1=2,A1D1=O′D1=1.求原四边形ABCD的面积.
【合作探究】
【探究二】 由直观图还原成原图
[解]如图,建立平面直角坐标系xOy,在x轴上截取OD=O′D1=1,OC=O′C1=2.
在过点D的y轴的平行线上截取DA=2D1A1=2.在过点A的x轴的平行线上截取AB=A1B1=2.连接BC,即得到了原图形(如图).由作法可知,原四边形ABCD是直角梯形,上、下底长度分别为AB=2,CD=3,直角腰长度为AD=2.所以面积为S=5.
【跟踪训练3】如图,矩形O′A′B′C′是水平放置的一个平面图形用斜二测画法得到的直观图,其中O′A′=6 cm,O′C′=2 cm,则原图形是( )
A.正方形 B.矩形
C.菱形 D.梯形
【答案】C解析:将直观图还原得到平行四边形OABC,如图所示,由题意知O′D′=O′C′=2 cm,OD=2O′D′=4 cm,C′D′=O′C′=2 cm,∴CD=2 cm,OC==6 cm,又OA=O′A′=6 cm,∴OA=OC,∴原图形为菱形.
【合作探究】
【探究三】 由直观图还原成原图
【拓展延伸】
【探究四】 有关直观图与原图的计算问题
【例4】已知用斜二测画法,画得的正方形的直观图面积为 ,则原正方形的面积为________.
【解】如图所示,作出正方形OABC的直观图O′A′B′C′,
作C′D′⊥x′轴于点D′.
【跟踪训练4】已知ΔABC的平面直观图ΔA′B′C′是边长为a的等边三角形,那么ΔABC的面积为( )
【拓展延伸】
【探究四】 有关直观图与原图的计算问题
【解】如图①为直观图,②为实际图形,
C
分析 求直观图的面积的关键是依据斜二测画法,求出相应的直观图的底边和高.
解析 如图①为直观图,②为实际图形,取B′C′所在直线为x′轴,过B′C′中点O′与O′x′成45°的直线为y′轴,过点A′作A′N′∥O′x′.交y′轴于点N′,过点A′作A′M′∥O′y′,交x′轴于点M′,
解析答案
解后反思
则在Rt△A′O′M′中,
答案 C
1
2
3
4
5
1.用斜二测画法画水平放置的平面图形的直观图,对其中的线段说法错误的是( )
A.原来相交的仍相交 B.原来垂直的仍垂直
C.原来平行的仍平行 D.原来共点的仍共点
B
【随堂训练】
2.如图所示为某一平面图形的直观图,则此平面图形可能是( )
C
1
2
3
4
5
3.已知等边三角形ABC的边长为a,那么等边三角形ABC的直观图△A′B′C′的面积为( )
D
4.如图,平行四边形O′P′Q′R′是四边形OPQR的直观图,若O′P′=3,O′R′=1,则原四边形OPQR的周长为_____.
10
5.已知如图所示的直观图△A′O′B′,则其
平面图形的面积为____.
6
【随堂训练】
1
2
3
4
5
解析答案
解析 方法一 建立如图①所示的平面直角坐标系xOy.
1
2
3
4
5
答案 D
1.水平放置平面图形直观图斜二测画法步骤:画轴取轴——取点——连线成图口诀:横不变纵减半,平行性不变2.空间几何体直观图斜二测画法步骤:画轴——画底面——画侧棱——连线成图口诀:横竖不变纵减半,平行性不变3.原图形的面积和直观图面积的关系:
【课时小结】
【作业布置】
【作业】
横格本:教科书P111-112,T1-T7.
必刷题:P60-61.
感谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
