人教版2023年七年级下册5.2 平行线及其判定 常考同步题型训练(含详解)
文档属性
| 名称 | 人教版2023年七年级下册5.2 平行线及其判定 常考同步题型训练(含详解) |  | |
| 格式 | doc | ||
| 文件大小 | 285.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 13:25:50 | ||
图片预览



文档简介
人教版2023年七年级下册5.2 平行线及其判定 常考同步题型训练
一.选择题
1.如图,能判定AD∥BC的是( )
A.∠1=∠2 B.∠1=∠3
C.∠3=∠4 D.∠B+∠BCD=180°
2.若将一副三角板按如图所示的方式放置,则下列结论正确的是( )
A.∠1=∠2 B.如果∠2=30°,则有AC∥DE
C.如果∠2=45°,则有∠4=∠D D.如果∠2=50°,则有BC∥AE
3.如图,下列推理中,正确的是( )
A.因为∠1=∠3,所以AB∥CD B.因为∠1=∠3,所以AE∥CF
C.因为∠2=∠4,所以AB∥CD D.因为∠2=∠4,所以AE∥CF
4.如图,在△ABC中,点D,E,F分别在边BC,AB,AC上,下列不能判定DE∥AC的条件是( )
A.∠3=∠C B.∠1+∠4=180° C.∠1=∠AFE D.∠1+∠2=180°
5.如图,将木条a,b与c钉在一起,∠1=85°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是( )
A.15° B.25° C.35° D.50°
6.如图,直线a、b被直线c所截,则下列式子:①∠1=∠8;②∠1=∠2;③∠3=∠6;④∠5+∠8=180°,能说明a∥b的条件的是( )
A.①② B.②④ C.①②③ D.①②③④
二.填空题
7.如图,请添加一个合适的条件 ,使AB∥CD.
8.如图是利用直尺和三角板过直线l外一点P作直线l的平行线的方法,这样做的依据是 .
9.如图,由∠A+∠B=180°,可得:AD∥BC.理由是 .
10.在同一平面内有三条直线l1、l2、l3,若l1⊥l2,l2⊥l3,则l1与13的位置关系是 .
11.如图,平面反光镜AC斜放在地面AB上,一束光线从地面上的P点射出,DE是反射光线.已知∠APD=120°,若要使反射光线DE∥AB,则∠CAB应调节为 度.
12.如图,直线EF上有两点A、C,分别引两条射线AB、CD.∠BAF=100°,CD与AB在直线EF异侧.若∠DCF=60°,射线AB、CD分别绕A点,C点以1度/秒和6度/秒的速度同时顺时针转动,设时间为t秒,在射线CD转动一周的时间内,当时间t的值为 时,CD与AB平行.
三.解答题
13.已知:如图,∠B=80°,∠C=50°,AC平分∠BAF.求证:EF∥BC.
14.如图,点G在CD上,已知∠BAG+∠AGD=180°,EA平分∠BAG,FG平分∠AGC,请说明AE∥GF的理由.
解:因为∠BAG+∠AGD=180°( ),
∠AGC+∠AGD=180°( ),
所以∠BAG=∠AGC( ).
因为EA平分∠BAG,
所以∠1= ( ).
因为FG平分∠AGC,
所以∠2= ,
得∠1=∠2( ),
所以AE∥GF( ).
15.如图,点E、F分别是AB、CD上的点,连接BD、AD、EC、BF,AD分别交CE、BF于点G、H,若∠DHF=∠AGE,∠ABF=∠C,求证:AB∥CD.
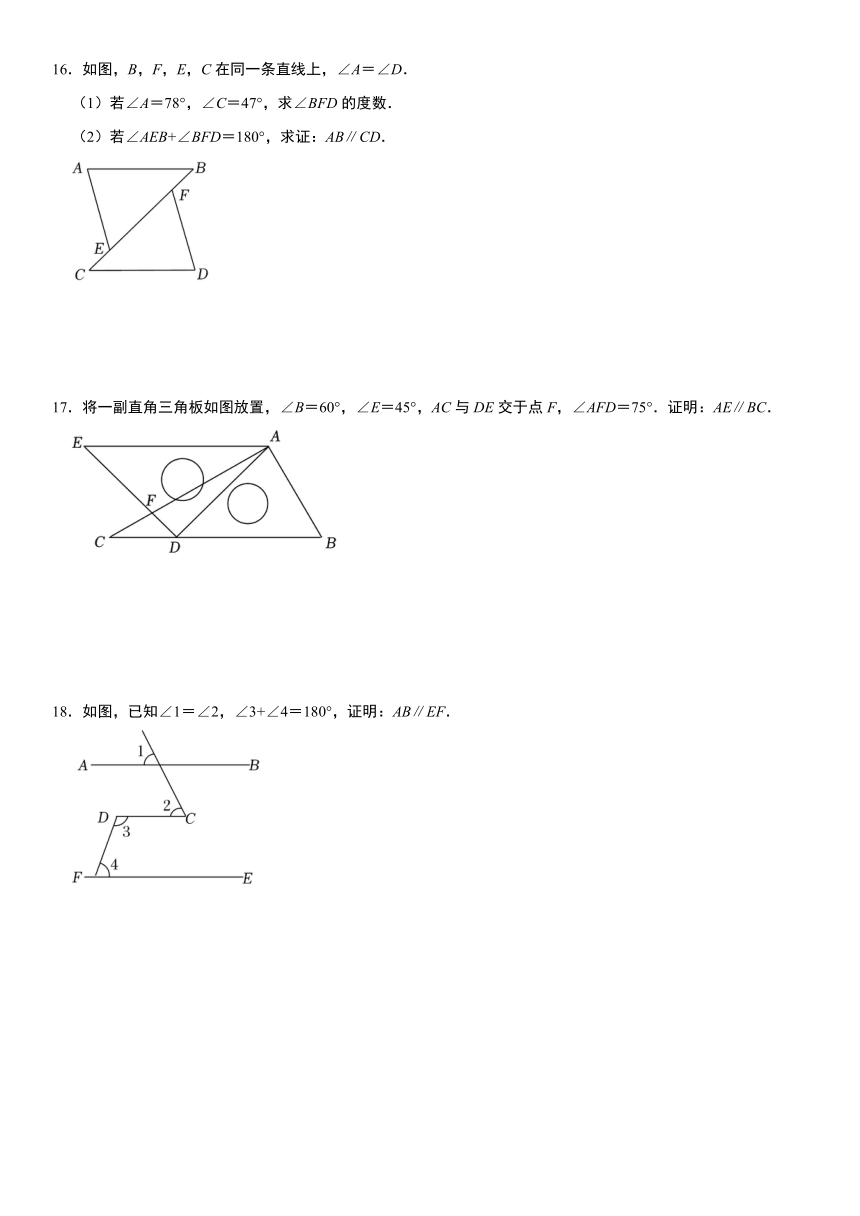
16.如图,B,F,E,C在同一条直线上,∠A=∠D.
(1)若∠A=78°,∠C=47°,求∠BFD的度数.
(2)若∠AEB+∠BFD=180°,求证:AB∥CD.
17.将一副直角三角板如图放置,∠B=60°,∠E=45°,AC与DE交于点F,∠AFD=75°.证明:AE∥BC.
18.如图,已知∠1=∠2,∠3+∠4=180°,证明:AB∥EF.
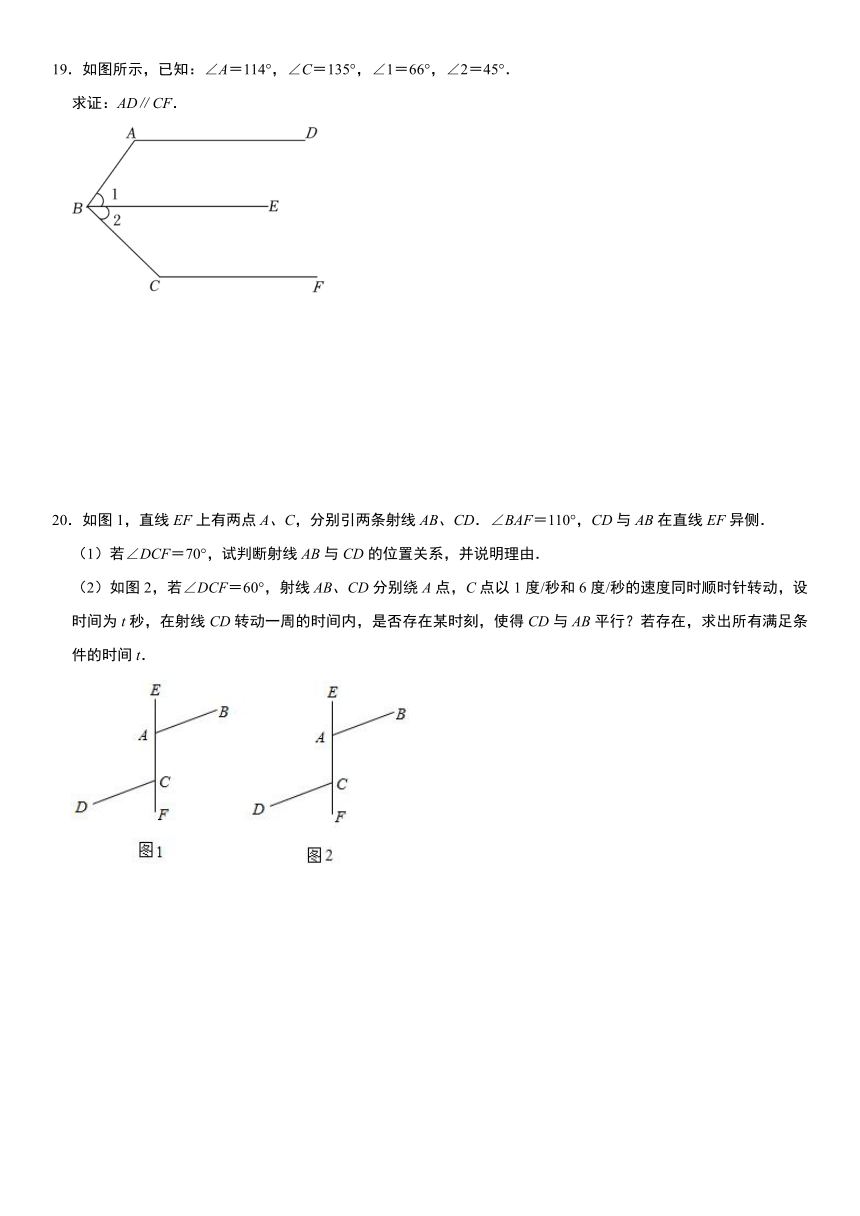
19.如图所示,已知:∠A=114°,∠C=135°,∠1=66°,∠2=45°.
求证:AD∥CF.
20.如图1,直线EF上有两点A、C,分别引两条射线AB、CD.∠BAF=110°,CD与AB在直线EF异侧.
(1)若∠DCF=70°,试判断射线AB与CD的位置关系,并说明理由.
(2)如图2,若∠DCF=60°,射线AB、CD分别绕A点,C点以1度/秒和6度/秒的速度同时顺时针转动,设时间为t秒,在射线CD转动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.
参考答案
一.选择题
1.【解答】解:∵∠1=∠2,
∴AD∥BC,
故A符合题意;
由∠1=∠3不能判定AD∥BC,
故B不符合题意;
由∠3=∠4,
∴AB∥DC,
故C不符合题意;
∵∠B+∠BCD=180°,
∴AB∥CD,
故D不符合题意;
故选:A.
2.【解答】解:∵∠CAB=∠DAE=90°,
∴∠1=∠3,故A错误.
∵∠2=30°,
∴∠1=∠3=60°
∴∠CAE=90°+60°=150°,
∴∠E+∠CAE=180°,
∴AC∥DE,故B正确,
∵∠2=45°,
∴∠1=∠2=∠3=45°,
∵∠E+∠3=∠B+∠4,
∴∠4=30°,
∵∠D=60°,
∴∠4≠∠D,故C错误,
∵∠2=50°,
∴∠3=40°,
∴∠B≠∠3,
∴BC不平行AE,故D错误.
故选:B.
3.【解答】解:A.由∠1=∠3,不能得到AB∥CD,故本选项错误;
B.由∠1=∠3,不能得到AE∥CF,故本选项错误;
C.由∠2=∠4,不能得到AB∥CD,故本选项错误;
D.由∠2=∠4,可以得到AE∥CF,故本选项正确;
故选:D.
4.【解答】解:A、当∠C=∠3时,DE∥AC,故不符合题意;
B、当∠1+∠4=180°时,DE∥AC,故不符合题意;
C、当∠1=∠AFE时,DE∥AC,故不符合题意;
D、当∠1+∠2=180°时,EF∥BC,不能判定DE∥AC,故符合题意.
故选:D.
5.【解答】解:∵∠AOC=∠2=50°时,OA∥b,
∴要使木条a与b平行,木条a旋转的度数至少是85°﹣50°=35°.
故选:C.
6.【解答】解:①同位角∠1=∠2;
②内错角∠3=∠6;
③对顶角∠1=∠7,又∠1=∠8,故同位角∠7=∠8;
④∠5+∠8=180°,邻补角∠5+∠7=180°,故同位角∠7=∠8;
四个条件都可以判定a∥b.
故选:D.
二.填空题
7.【解答】解:当∠DCE=∠ABC时,根据同位角相等,两直线平行可得AB∥CD;
当∠DCA=∠CAB时,根据内错角相等,两直线平行可得AB∥CD;
当∠DCB+∠ABC=180°时,根据同旁内角互补,两直线平行可得AB∥CD.
故答案为:∠DCE=∠ABC或∠DCA=∠CAB或∠DCB+∠ABC=180°(任填一个即可).
8.【解答】解:由图形得,有两个相等的同位角存在,
这样做的依据是:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
9.【解答】解:由∠A+∠B=180°,可得:AD∥BC,理由是同旁内角互补,两直线平行;
故答案为:同旁内角互补,两直线平行.
10.【解答】解:∵在同一平面内,l1⊥l2,l2⊥l3,
∴l1∥l3,
即l1与l3的位置关系是平行,
故答案为:平行.
11.【解答】解:要使反射光线DE∥AB,
则∠APD=∠PDE,
∵∠APD=120°,
∴∠PDE=120°,
∵∠ADP=∠CDE,∠ADP+∠PDE+∠CDE=180°,
∴∠ADP=∠CDE=30°,
∴∠CAB=180°﹣∠APD﹣∠ADP=30°,
故答案为:30.
12.【解答】解:分三种情况:
如图①,AB与CD在EF的两侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠ACD=180°﹣60°﹣(6t)°=120°﹣(6t)°,∠BAC=100°﹣t°,
要使AB∥CD,则∠ACD=∠BAF,
即120°﹣(6t)°=100°﹣t°,
解得t=4;
此时(180°﹣60°)÷6=20,
∴0<t<20;
②CD旋转到与AB都在EF的右侧时,
∵∠BAF=100°,∠DCF=60°,
∴∠DCF=360°﹣(6t)°﹣60°=300°﹣(6t)°,∠BAC=100°﹣t°,
要使AB∥CD,则∠DCF=∠BAC,
即300°﹣(6t)°=100°﹣t°,
解得t=40,
此时(360°﹣60°)÷6=50,
∴20<t<50;
③CD旋转到与AB都在EF的左侧时,
∵∠BAF=100°,∠DCF=60°,
∴∠DCF=(6t)°﹣(180°﹣60°+180°)=(6t)°﹣300°,∠BAC=t°﹣100°,
要使AB∥CD,则∠DCF=∠BAC,
即(6t)°﹣300°=t°﹣100°,
解得t=40,
此时t>50,
∵40<50,
∴此情况不存在.
综上所述,当时间t的值为4秒或40秒时,CD与AB平行.
故答案为:4秒或40秒.
三.解答题
13.【解答】证明:∵∠B=80°,∠C=50°,
∴∠BAC=180°﹣∠A﹣∠B=50°,
∵AC平分∠BAF,
∴∠BAC=∠CAF=50°,
∴∠C=∠CAF,
∴EF∥BC.
14.【解答】解:因为∠BAG+∠AGD=180°(已知),
∠AGC+∠AGD=180°(邻补角的定义),
所以∠BAG=∠AGC(同角的补角相等),
因为EA平分∠BAG,
所以∠1=∠BAG(角平分线的定义),
因为FG平分∠AGC,
所以∠2=∠AGC,
得∠1=∠2(等量代换),
所以AE∥GF(内错角相等,两直线平行).
故答案为:已知;邻补角的定义;同角的补角相等;∠BAG;角平分线的定义;∠AGC;等量代换;内错角相等,两直线平行.
15.【解答】证明:∵∠DHF=∠AHB,∠DHF=∠AGE,
∴∠AHB=∠AGE,
∴BH∥EC,
∴∠ABF=∠AEG,
∴∠ABF=∠C,
∴∠AEG=∠C,
∴AB∥CD.
16.【解答】(1)解:∵∠A=78°,∠A=∠D,
∴∠D=78°,
∵∠C=47°,
∴∠BFD=∠D+∠C=78°+47°=125°;
(2)证明:∵∠AEB+∠BFD=180°,∠CFD+∠BFD=180°,
∴∠AEB=∠CFD,
∵∠A=∠D,
∴(180°﹣∠A﹣∠B)+(∠C+∠D)=180°,
∴∠B=∠C,
∴AB∥CD.
17.【解答】证明:∵直角三角板ABC,∠B=60°,
∴∠C=30°,
∵∠AFD=75°,∠AFD是△CDF的外角,
∴∠CDE=∠AFD﹣∠C=45°,
∵∠E=45°,
∴∠E=∠CDE,
∴AE∥BC.
18.【解答】证明:∵∠1=∠2,
∴AB∥CD.
∵∠3+∠4=180°,
∴CD∥EF.
∴AB∥EF.
19.【解答】证明:∵∠A=114°,∠C=135°,∠1=66°,∠2=45°,
∴∠A+∠1=114°+66°=180°,∠C+∠2=135°+45°=180°,
∴AD∥BE,CD∥BE,
∴AD∥CF.
20.【解答】解:(1)AB∥CD,
理由:∵∠DCF=70°,
∴∠ACD=180°﹣∠DCF=110°,
∵∠BAF=110°,
∴∠BAF=∠ACD,
∴AB∥CD;
(2)解:存在.分三种情况:
如图①,AB与CD在EF的两侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠ACD=180°﹣60°﹣(6t)°=120°﹣(6t)°,∠BAC=110°﹣t°,
要使AB∥CD,则∠ACD=∠BAF,
即120°﹣(6t)°=110°﹣t°,
解得t=2;
此时(180°﹣60°)÷6=20,
∴0<t<20;
②CD旋转到与AB都在EF的右侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠DCF=360°﹣(6t)°﹣60°=300°﹣(6t)°,∠BAC=110°﹣t°,
要使AB∥CD,则∠DCF=∠BAC,
即300°﹣(6t)°=110°﹣t°,
解得t=38,
此时(360°﹣60°)÷6=50,
∴20<t<50;
③CD旋转到与AB都在EF的左侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠DCF=(6t)°﹣(180°﹣60°+180°)=(6t)°﹣300°,∠BAC=t°﹣110°,
要使AB∥CD,则∠DCF=∠BAC,
即(6t)°﹣300°=t°﹣110°,
解得t=38,
此时t>50,
∵38<50,
∴此情况不存在.
综上所述,t为2秒或38秒时,CD与AB平行.
一.选择题
1.如图,能判定AD∥BC的是( )
A.∠1=∠2 B.∠1=∠3
C.∠3=∠4 D.∠B+∠BCD=180°
2.若将一副三角板按如图所示的方式放置,则下列结论正确的是( )
A.∠1=∠2 B.如果∠2=30°,则有AC∥DE
C.如果∠2=45°,则有∠4=∠D D.如果∠2=50°,则有BC∥AE
3.如图,下列推理中,正确的是( )
A.因为∠1=∠3,所以AB∥CD B.因为∠1=∠3,所以AE∥CF
C.因为∠2=∠4,所以AB∥CD D.因为∠2=∠4,所以AE∥CF
4.如图,在△ABC中,点D,E,F分别在边BC,AB,AC上,下列不能判定DE∥AC的条件是( )
A.∠3=∠C B.∠1+∠4=180° C.∠1=∠AFE D.∠1+∠2=180°
5.如图,将木条a,b与c钉在一起,∠1=85°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是( )
A.15° B.25° C.35° D.50°
6.如图,直线a、b被直线c所截,则下列式子:①∠1=∠8;②∠1=∠2;③∠3=∠6;④∠5+∠8=180°,能说明a∥b的条件的是( )
A.①② B.②④ C.①②③ D.①②③④
二.填空题
7.如图,请添加一个合适的条件 ,使AB∥CD.
8.如图是利用直尺和三角板过直线l外一点P作直线l的平行线的方法,这样做的依据是 .
9.如图,由∠A+∠B=180°,可得:AD∥BC.理由是 .
10.在同一平面内有三条直线l1、l2、l3,若l1⊥l2,l2⊥l3,则l1与13的位置关系是 .
11.如图,平面反光镜AC斜放在地面AB上,一束光线从地面上的P点射出,DE是反射光线.已知∠APD=120°,若要使反射光线DE∥AB,则∠CAB应调节为 度.
12.如图,直线EF上有两点A、C,分别引两条射线AB、CD.∠BAF=100°,CD与AB在直线EF异侧.若∠DCF=60°,射线AB、CD分别绕A点,C点以1度/秒和6度/秒的速度同时顺时针转动,设时间为t秒,在射线CD转动一周的时间内,当时间t的值为 时,CD与AB平行.
三.解答题
13.已知:如图,∠B=80°,∠C=50°,AC平分∠BAF.求证:EF∥BC.
14.如图,点G在CD上,已知∠BAG+∠AGD=180°,EA平分∠BAG,FG平分∠AGC,请说明AE∥GF的理由.
解:因为∠BAG+∠AGD=180°( ),
∠AGC+∠AGD=180°( ),
所以∠BAG=∠AGC( ).
因为EA平分∠BAG,
所以∠1= ( ).
因为FG平分∠AGC,
所以∠2= ,
得∠1=∠2( ),
所以AE∥GF( ).
15.如图,点E、F分别是AB、CD上的点,连接BD、AD、EC、BF,AD分别交CE、BF于点G、H,若∠DHF=∠AGE,∠ABF=∠C,求证:AB∥CD.
16.如图,B,F,E,C在同一条直线上,∠A=∠D.
(1)若∠A=78°,∠C=47°,求∠BFD的度数.
(2)若∠AEB+∠BFD=180°,求证:AB∥CD.
17.将一副直角三角板如图放置,∠B=60°,∠E=45°,AC与DE交于点F,∠AFD=75°.证明:AE∥BC.
18.如图,已知∠1=∠2,∠3+∠4=180°,证明:AB∥EF.
19.如图所示,已知:∠A=114°,∠C=135°,∠1=66°,∠2=45°.
求证:AD∥CF.
20.如图1,直线EF上有两点A、C,分别引两条射线AB、CD.∠BAF=110°,CD与AB在直线EF异侧.
(1)若∠DCF=70°,试判断射线AB与CD的位置关系,并说明理由.
(2)如图2,若∠DCF=60°,射线AB、CD分别绕A点,C点以1度/秒和6度/秒的速度同时顺时针转动,设时间为t秒,在射线CD转动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.
参考答案
一.选择题
1.【解答】解:∵∠1=∠2,
∴AD∥BC,
故A符合题意;
由∠1=∠3不能判定AD∥BC,
故B不符合题意;
由∠3=∠4,
∴AB∥DC,
故C不符合题意;
∵∠B+∠BCD=180°,
∴AB∥CD,
故D不符合题意;
故选:A.
2.【解答】解:∵∠CAB=∠DAE=90°,
∴∠1=∠3,故A错误.
∵∠2=30°,
∴∠1=∠3=60°
∴∠CAE=90°+60°=150°,
∴∠E+∠CAE=180°,
∴AC∥DE,故B正确,
∵∠2=45°,
∴∠1=∠2=∠3=45°,
∵∠E+∠3=∠B+∠4,
∴∠4=30°,
∵∠D=60°,
∴∠4≠∠D,故C错误,
∵∠2=50°,
∴∠3=40°,
∴∠B≠∠3,
∴BC不平行AE,故D错误.
故选:B.
3.【解答】解:A.由∠1=∠3,不能得到AB∥CD,故本选项错误;
B.由∠1=∠3,不能得到AE∥CF,故本选项错误;
C.由∠2=∠4,不能得到AB∥CD,故本选项错误;
D.由∠2=∠4,可以得到AE∥CF,故本选项正确;
故选:D.
4.【解答】解:A、当∠C=∠3时,DE∥AC,故不符合题意;
B、当∠1+∠4=180°时,DE∥AC,故不符合题意;
C、当∠1=∠AFE时,DE∥AC,故不符合题意;
D、当∠1+∠2=180°时,EF∥BC,不能判定DE∥AC,故符合题意.
故选:D.
5.【解答】解:∵∠AOC=∠2=50°时,OA∥b,
∴要使木条a与b平行,木条a旋转的度数至少是85°﹣50°=35°.
故选:C.
6.【解答】解:①同位角∠1=∠2;
②内错角∠3=∠6;
③对顶角∠1=∠7,又∠1=∠8,故同位角∠7=∠8;
④∠5+∠8=180°,邻补角∠5+∠7=180°,故同位角∠7=∠8;
四个条件都可以判定a∥b.
故选:D.
二.填空题
7.【解答】解:当∠DCE=∠ABC时,根据同位角相等,两直线平行可得AB∥CD;
当∠DCA=∠CAB时,根据内错角相等,两直线平行可得AB∥CD;
当∠DCB+∠ABC=180°时,根据同旁内角互补,两直线平行可得AB∥CD.
故答案为:∠DCE=∠ABC或∠DCA=∠CAB或∠DCB+∠ABC=180°(任填一个即可).
8.【解答】解:由图形得,有两个相等的同位角存在,
这样做的依据是:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
9.【解答】解:由∠A+∠B=180°,可得:AD∥BC,理由是同旁内角互补,两直线平行;
故答案为:同旁内角互补,两直线平行.
10.【解答】解:∵在同一平面内,l1⊥l2,l2⊥l3,
∴l1∥l3,
即l1与l3的位置关系是平行,
故答案为:平行.
11.【解答】解:要使反射光线DE∥AB,
则∠APD=∠PDE,
∵∠APD=120°,
∴∠PDE=120°,
∵∠ADP=∠CDE,∠ADP+∠PDE+∠CDE=180°,
∴∠ADP=∠CDE=30°,
∴∠CAB=180°﹣∠APD﹣∠ADP=30°,
故答案为:30.
12.【解答】解:分三种情况:
如图①,AB与CD在EF的两侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠ACD=180°﹣60°﹣(6t)°=120°﹣(6t)°,∠BAC=100°﹣t°,
要使AB∥CD,则∠ACD=∠BAF,
即120°﹣(6t)°=100°﹣t°,
解得t=4;
此时(180°﹣60°)÷6=20,
∴0<t<20;
②CD旋转到与AB都在EF的右侧时,
∵∠BAF=100°,∠DCF=60°,
∴∠DCF=360°﹣(6t)°﹣60°=300°﹣(6t)°,∠BAC=100°﹣t°,
要使AB∥CD,则∠DCF=∠BAC,
即300°﹣(6t)°=100°﹣t°,
解得t=40,
此时(360°﹣60°)÷6=50,
∴20<t<50;
③CD旋转到与AB都在EF的左侧时,
∵∠BAF=100°,∠DCF=60°,
∴∠DCF=(6t)°﹣(180°﹣60°+180°)=(6t)°﹣300°,∠BAC=t°﹣100°,
要使AB∥CD,则∠DCF=∠BAC,
即(6t)°﹣300°=t°﹣100°,
解得t=40,
此时t>50,
∵40<50,
∴此情况不存在.
综上所述,当时间t的值为4秒或40秒时,CD与AB平行.
故答案为:4秒或40秒.
三.解答题
13.【解答】证明:∵∠B=80°,∠C=50°,
∴∠BAC=180°﹣∠A﹣∠B=50°,
∵AC平分∠BAF,
∴∠BAC=∠CAF=50°,
∴∠C=∠CAF,
∴EF∥BC.
14.【解答】解:因为∠BAG+∠AGD=180°(已知),
∠AGC+∠AGD=180°(邻补角的定义),
所以∠BAG=∠AGC(同角的补角相等),
因为EA平分∠BAG,
所以∠1=∠BAG(角平分线的定义),
因为FG平分∠AGC,
所以∠2=∠AGC,
得∠1=∠2(等量代换),
所以AE∥GF(内错角相等,两直线平行).
故答案为:已知;邻补角的定义;同角的补角相等;∠BAG;角平分线的定义;∠AGC;等量代换;内错角相等,两直线平行.
15.【解答】证明:∵∠DHF=∠AHB,∠DHF=∠AGE,
∴∠AHB=∠AGE,
∴BH∥EC,
∴∠ABF=∠AEG,
∴∠ABF=∠C,
∴∠AEG=∠C,
∴AB∥CD.
16.【解答】(1)解:∵∠A=78°,∠A=∠D,
∴∠D=78°,
∵∠C=47°,
∴∠BFD=∠D+∠C=78°+47°=125°;
(2)证明:∵∠AEB+∠BFD=180°,∠CFD+∠BFD=180°,
∴∠AEB=∠CFD,
∵∠A=∠D,
∴(180°﹣∠A﹣∠B)+(∠C+∠D)=180°,
∴∠B=∠C,
∴AB∥CD.
17.【解答】证明:∵直角三角板ABC,∠B=60°,
∴∠C=30°,
∵∠AFD=75°,∠AFD是△CDF的外角,
∴∠CDE=∠AFD﹣∠C=45°,
∵∠E=45°,
∴∠E=∠CDE,
∴AE∥BC.
18.【解答】证明:∵∠1=∠2,
∴AB∥CD.
∵∠3+∠4=180°,
∴CD∥EF.
∴AB∥EF.
19.【解答】证明:∵∠A=114°,∠C=135°,∠1=66°,∠2=45°,
∴∠A+∠1=114°+66°=180°,∠C+∠2=135°+45°=180°,
∴AD∥BE,CD∥BE,
∴AD∥CF.
20.【解答】解:(1)AB∥CD,
理由:∵∠DCF=70°,
∴∠ACD=180°﹣∠DCF=110°,
∵∠BAF=110°,
∴∠BAF=∠ACD,
∴AB∥CD;
(2)解:存在.分三种情况:
如图①,AB与CD在EF的两侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠ACD=180°﹣60°﹣(6t)°=120°﹣(6t)°,∠BAC=110°﹣t°,
要使AB∥CD,则∠ACD=∠BAF,
即120°﹣(6t)°=110°﹣t°,
解得t=2;
此时(180°﹣60°)÷6=20,
∴0<t<20;
②CD旋转到与AB都在EF的右侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠DCF=360°﹣(6t)°﹣60°=300°﹣(6t)°,∠BAC=110°﹣t°,
要使AB∥CD,则∠DCF=∠BAC,
即300°﹣(6t)°=110°﹣t°,
解得t=38,
此时(360°﹣60°)÷6=50,
∴20<t<50;
③CD旋转到与AB都在EF的左侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠DCF=(6t)°﹣(180°﹣60°+180°)=(6t)°﹣300°,∠BAC=t°﹣110°,
要使AB∥CD,则∠DCF=∠BAC,
即(6t)°﹣300°=t°﹣110°,
解得t=38,
此时t>50,
∵38<50,
∴此情况不存在.
综上所述,t为2秒或38秒时,CD与AB平行.
