【新课标】1.4.2角平分线 课件(共22张PPT)
文档属性
| 名称 | 【新课标】1.4.2角平分线 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
1.4.2角平分线
北师版八年级下册
教学目标
1.能够证明三角形的三条角平分线交于一点且这一点到三条边的距离相等.
2.角平分线的性质定理和判定定理的灵活运用.
新知导入
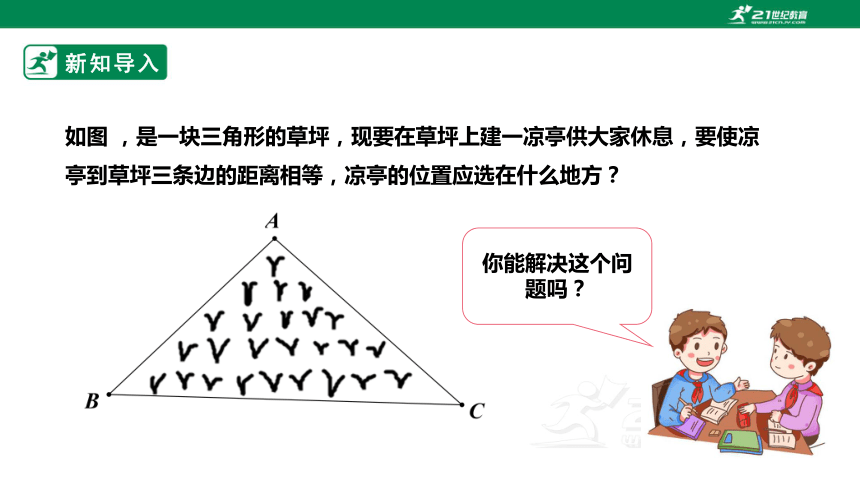
如图 ,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在什么地方?
你能解决这个问题吗?
新知讲解
在练习本上任意画出一个三角形
画出三角形三条角平分线。你发现了什么?
三角形的三条角平分线相交于一点.
新知讲解
分别过交点作三角形三边的垂线,你能发现什么?
过交点作三角形三边的垂线段相等.
综上你能得出什么结论?
三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
怎样证明上面的结论?
典例精析
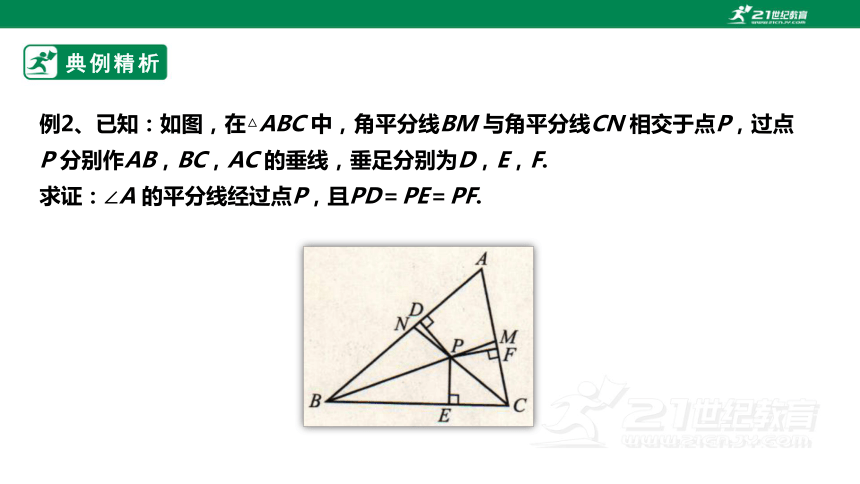
例2、已知:如图,在△ABC 中,角平分线BM 与角平分线CN 相交于点P,过点P 分别作AB,BC,AC 的垂线,垂足分别为D,E,F.
求证:∠A 的平分线经过点P,且PD=PE=PF.
新知讲解
证明:∵BM 是△ABC 的角平分线,点P 在BM上,且PD丄AB,PE丄BC,垂足分别为D,E,
∴PD=PE (角平分线上的点到这个角的两边的距离相等).
同理,PE=PF.
∴PD=PE=PF.
∴点P 在∠A 的平分线上(在一个角的内部,到角的两边距离相等的点在这个角的平分线上),
即∠A 的平分线经过点P.
归纳总结
A
B
C
P
E
D
F
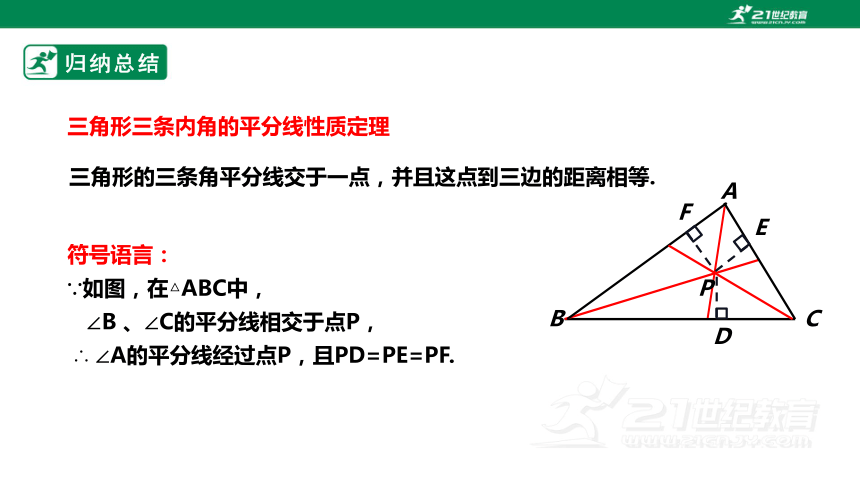
三角形的三条角平分线交于一点,并且这点到三边的距离相等.
符号语言:
∵如图,在△ABC中,
∠B 、∠C的平分线相交于点P,
∴ ∠A的平分线经过点P,且PD=PE=PF.
三角形三条内角的平分线性质定理
典例精析
例3、如图,在△ABC中,已知AC=BC, ∠C=90°, AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD.
E
D
A
B
C
(1)解:∵AD是△ABC的角平分线, DC⊥AC, DE⊥AB,垂足为E,
∴DE=CD=4cm.
∵AC=BC,∴∠B=∠BAC.
∵∠C=90°,∴∠B=45° ,∴∠BDE=45°.∴BE=DE.
在等腰直角三角形BDE中,cm
∴AC=BC=CD+BD=(4+4)cm
典例精析
(2)证明:由(1)的求解过程易知,
Rt△ACD ≌Rt△AED(HL).
∴AC=AE.
∵BE=DE=CD,
∴AB=AE+BE=AC+CD.
课堂练习
1.已知△ABC,求作一点P,使P 到∠A 的两边的距离相等,且PA=PB.下列确定P点的方法正确的是( )
A.P 为∠A 与∠B 的平分线的交点
B.P 为∠A 的平分线与AB 的垂直平分线的交点
C.P 为AC,AB 两边上的高的交点
D.P 为AC,AB 两边的垂直平分线的交点
B
课堂练习
2.如图,△ABC的三边AB,BC,AC的长分别为4,6,8,其三条角平分线将△ABC分成三个三角形,则S△OAB:S△OBC:S△OAC=( )
A.1∶1∶1 B.6∶4∶3
C.2∶3∶4 D.4∶3∶2
C
课堂练习
3. 已知,如图,在△ABC中,BP、CP分别是∠ABC和∠ACB的角平分线,且交于P,PD⊥AB,PE⊥ BC,PF ⊥CA,垂足分别为D、E、F,PD=2cm,则PE=_____,PF=_____.
2cm
2cm
4.如图,在△ABC 中,∠A=100°,若∠ABC 和∠ACB 的平分线交于点O,则∠BOC=________.
140°
课堂练习
5.已知:如图,在Rt△ABC中,∠ACB=90°, ∠B=60°,AD,CE是角平分线,
AD与CE 相交于点F,FM⊥AB,FN⊥BC,垂足分别为 M,N.
求证:FE=FD.
解:连接BF,由题意易知BF即为∠ABC的平分线,则FM=FN,
在Rt△ABC中,
∵∠B=60°,
∴∠BAC=30°.
∴∠DAB=∠BAC=15°.
课堂练习
∴∠FDN=∠DAB+∠B=75°,
∠FEM=∠BAC+∠ACE
=30°+∠ACB=30°+45°=75°.
∴∠FEM=∠FDN.
在△FEM与△FDN中,
∴△FEM ≌△FDN.
∴FE=FD.
课堂练习
6.如图,DE⊥AB于点E,DF⊥AC于点F,BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)猜想AB+AC与AE之间的数量关系,并给予证明.
(1)证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°.
在Rt△BDE和Rt△CDF中,
∵BD=CD,BE=CF,
∴Rt△BDE≌Rt△CDF,
∴DE=DF,∴AD平分∠BAC.
课堂练习
解:AB+AC=2AE.
证明:∵AD平分∠BAC,∴∠EAD=∠CAD.
在△AED与△AFD中,
∵∠EAD=∠FAD,∠AED=∠AFD=90°,AD=AD,∴△AED≌△AFD,
∴AE=AF.
∴AB+AC=AE-BE+AF+CF
=AE+AE=2AE.
课堂总结
三角形的内角平分线
性质
三角形的三条内角平分线相交于一点,并且这一点到三条边的距离相等
应用
判断一个点是否在角的平分线上;
解决实际问题
板书设计
1.4.2角平分线
1.三角形的三条角平分线的性质
2.例题讲解
作业布置
【必做题】
教材第32页习题1.10的1、2、3题
【选做题】
教材第32页习题1.10的4题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.4.2角平分线
北师版八年级下册
教学目标
1.能够证明三角形的三条角平分线交于一点且这一点到三条边的距离相等.
2.角平分线的性质定理和判定定理的灵活运用.
新知导入
如图 ,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在什么地方?
你能解决这个问题吗?
新知讲解
在练习本上任意画出一个三角形
画出三角形三条角平分线。你发现了什么?
三角形的三条角平分线相交于一点.
新知讲解
分别过交点作三角形三边的垂线,你能发现什么?
过交点作三角形三边的垂线段相等.
综上你能得出什么结论?
三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
怎样证明上面的结论?
典例精析
例2、已知:如图,在△ABC 中,角平分线BM 与角平分线CN 相交于点P,过点P 分别作AB,BC,AC 的垂线,垂足分别为D,E,F.
求证:∠A 的平分线经过点P,且PD=PE=PF.
新知讲解
证明:∵BM 是△ABC 的角平分线,点P 在BM上,且PD丄AB,PE丄BC,垂足分别为D,E,
∴PD=PE (角平分线上的点到这个角的两边的距离相等).
同理,PE=PF.
∴PD=PE=PF.
∴点P 在∠A 的平分线上(在一个角的内部,到角的两边距离相等的点在这个角的平分线上),
即∠A 的平分线经过点P.
归纳总结
A
B
C
P
E
D
F
三角形的三条角平分线交于一点,并且这点到三边的距离相等.
符号语言:
∵如图,在△ABC中,
∠B 、∠C的平分线相交于点P,
∴ ∠A的平分线经过点P,且PD=PE=PF.
三角形三条内角的平分线性质定理
典例精析
例3、如图,在△ABC中,已知AC=BC, ∠C=90°, AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD.
E
D
A
B
C
(1)解:∵AD是△ABC的角平分线, DC⊥AC, DE⊥AB,垂足为E,
∴DE=CD=4cm.
∵AC=BC,∴∠B=∠BAC.
∵∠C=90°,∴∠B=45° ,∴∠BDE=45°.∴BE=DE.
在等腰直角三角形BDE中,cm
∴AC=BC=CD+BD=(4+4)cm
典例精析
(2)证明:由(1)的求解过程易知,
Rt△ACD ≌Rt△AED(HL).
∴AC=AE.
∵BE=DE=CD,
∴AB=AE+BE=AC+CD.
课堂练习
1.已知△ABC,求作一点P,使P 到∠A 的两边的距离相等,且PA=PB.下列确定P点的方法正确的是( )
A.P 为∠A 与∠B 的平分线的交点
B.P 为∠A 的平分线与AB 的垂直平分线的交点
C.P 为AC,AB 两边上的高的交点
D.P 为AC,AB 两边的垂直平分线的交点
B
课堂练习
2.如图,△ABC的三边AB,BC,AC的长分别为4,6,8,其三条角平分线将△ABC分成三个三角形,则S△OAB:S△OBC:S△OAC=( )
A.1∶1∶1 B.6∶4∶3
C.2∶3∶4 D.4∶3∶2
C
课堂练习
3. 已知,如图,在△ABC中,BP、CP分别是∠ABC和∠ACB的角平分线,且交于P,PD⊥AB,PE⊥ BC,PF ⊥CA,垂足分别为D、E、F,PD=2cm,则PE=_____,PF=_____.
2cm
2cm
4.如图,在△ABC 中,∠A=100°,若∠ABC 和∠ACB 的平分线交于点O,则∠BOC=________.
140°
课堂练习
5.已知:如图,在Rt△ABC中,∠ACB=90°, ∠B=60°,AD,CE是角平分线,
AD与CE 相交于点F,FM⊥AB,FN⊥BC,垂足分别为 M,N.
求证:FE=FD.
解:连接BF,由题意易知BF即为∠ABC的平分线,则FM=FN,
在Rt△ABC中,
∵∠B=60°,
∴∠BAC=30°.
∴∠DAB=∠BAC=15°.
课堂练习
∴∠FDN=∠DAB+∠B=75°,
∠FEM=∠BAC+∠ACE
=30°+∠ACB=30°+45°=75°.
∴∠FEM=∠FDN.
在△FEM与△FDN中,
∴△FEM ≌△FDN.
∴FE=FD.
课堂练习
6.如图,DE⊥AB于点E,DF⊥AC于点F,BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)猜想AB+AC与AE之间的数量关系,并给予证明.
(1)证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°.
在Rt△BDE和Rt△CDF中,
∵BD=CD,BE=CF,
∴Rt△BDE≌Rt△CDF,
∴DE=DF,∴AD平分∠BAC.
课堂练习
解:AB+AC=2AE.
证明:∵AD平分∠BAC,∴∠EAD=∠CAD.
在△AED与△AFD中,
∵∠EAD=∠FAD,∠AED=∠AFD=90°,AD=AD,∴△AED≌△AFD,
∴AE=AF.
∴AB+AC=AE-BE+AF+CF
=AE+AE=2AE.
课堂总结
三角形的内角平分线
性质
三角形的三条内角平分线相交于一点,并且这一点到三条边的距离相等
应用
判断一个点是否在角的平分线上;
解决实际问题
板书设计
1.4.2角平分线
1.三角形的三条角平分线的性质
2.例题讲解
作业布置
【必做题】
教材第32页习题1.10的1、2、3题
【选做题】
教材第32页习题1.10的4题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
