人教版2023年七年级下册 5.3 平行线的性质 同步类常见题型训练卷(含详解)
文档属性
| 名称 | 人教版2023年七年级下册 5.3 平行线的性质 同步类常见题型训练卷(含详解) |  | |
| 格式 | doc | ||
| 文件大小 | 312.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 13:26:58 | ||
图片预览



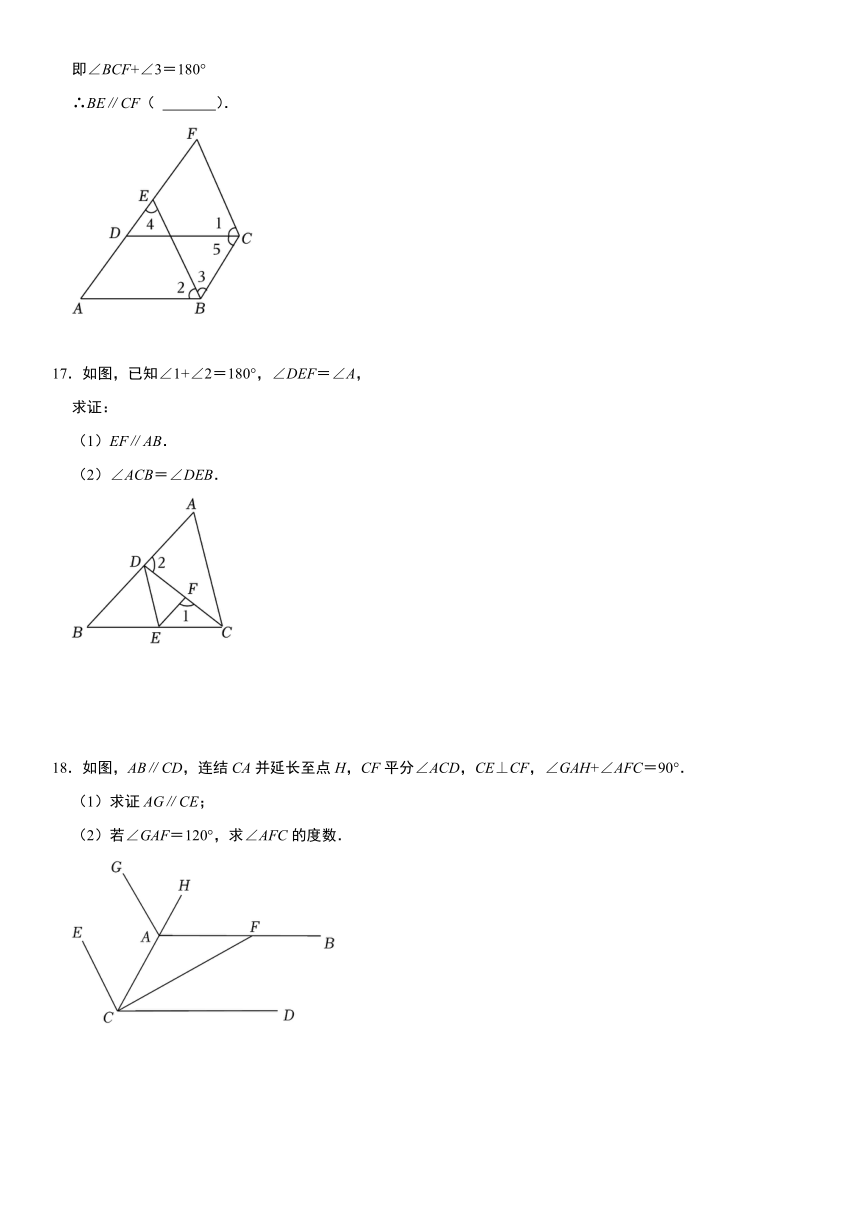
文档简介
人教版2023年七年级下册 5.3 平行线的性质 同步类常见题型训练卷
一.选择题
1.如图,两条平行线a,b被第三条直线c所截.若∠2=56°,则∠1的度数为( )
A.120° B.112° C.124° D.56°
2.如图,已知OP平分∠AOB,∠AOB=30°,PC∥OA,则∠CPO为( )
A.30° B.10° C.15° D.5°
3.把一块直尺与一块三角板如图放置,若∠1=38°,则∠2的度数是( )
A.128° B.138° C.142° D.152°
4.如图,已知a∥b,则∠ACD的度数是( )
A.45° B.60° C.73° D.90°
5.如图,AB∥CD,∠ABE=125°,∠C=30°,则∠α=( )
A.70° B.75° C.80° D.85°
6.如图,AB∥CD,一副三角尺按如图所示放置,∠AEG=20°,则∠HFD的度数为( )
A.40° B.35° C.30° D.25°
7.下列语句属于命题的是( )
A.你今天打卡了吗? B.请戴好口罩!
C.画出两条相等的线段 D.同位角相等
8.下列命题是真命题的是( )
A.同位角相等
B.内错角相等
C.相等的角是对顶角
D.同旁内角互补,两直线平行
二.填空题
9.命题“内错角相等,两直线平行”是 (填“真”或“假”)命题.
10.把下列命题改写成“如果……,那么……”的形式:同角的补角相等.改写成 .
11.生活中常见的探照灯、汽车大灯等灯具都是凹面镜.如图,从光源P点照射到凹面镜上的光线PA、PB等反射以后沿着与直线PF平行的方向射出,若∠CAP=36°,∠DBP=58°,则∠APB的度数为 .
12.如图,把一个长方形纸片沿OG折叠后,C,D两点分别落在C',D'两点处,若∠AOD':∠D'OG=4:3,则∠BGO= 度.
13.如图,AB∥CD,∠1+∠2=110°,则∠GEF+∠GFE= .
14.如图,给出下列命题:①∵∠1=∠2,∴AB∥DC; ②∵∠4=∠5,∴AD∥BC; ③∵∠ABC+∠ACB+∠2=180°,∴AB∥CD; ④∵∠3=∠ABD,∴AD∥BC,其中正确的命题有 .
三.解答题
15.如图,若AB∥DE,AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由.
解:∠A+∠D=180°.
理由如下:
∵AB∥DE( )
∴∠A= ( )
∵AC∥DF( )
∴∠D+ =180°( )
∴∠A+∠D=180°( )
16.如图,已知∠1=∠2,∠3=∠4,∠5=∠A,试说明:BE∥CF.
完善下面的解答过程,并填写理由或数学式:解:
∵∠3=∠4(已知)
∴AE∥ ( )
∴∠EDC=∠5( )
∵∠5=∠A(已知)
∴∠EDC= (等量代换)
∴DC∥AB( )
∴∠5+∠ABC=180°( )
即∠5+∠2+∠3=180°
∵∠1=∠2(已知)
∴∠5+∠1+∠3=180°( )
即∠BCF+∠3=180°
∴BE∥CF( ).
17.如图,已知∠1+∠2=180°,∠DEF=∠A,
求证:
(1)EF∥AB.
(2)∠ACB=∠DEB.
18.如图,AB∥CD,连结CA并延长至点H,CF平分∠ACD,CE⊥CF,∠GAH+∠AFC=90°.
(1)求证AG∥CE;
(2)若∠GAF=120°,求∠AFC的度数.
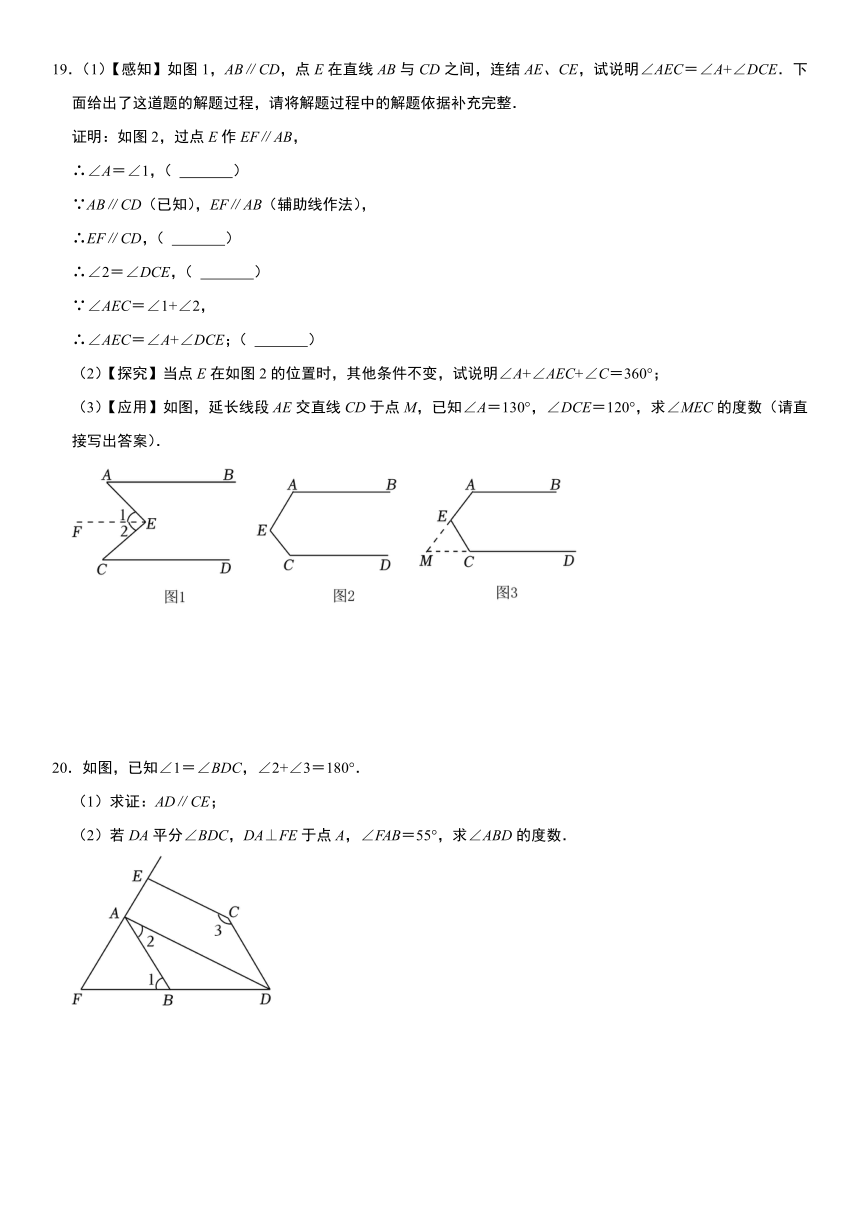
19.(1)【感知】如图1,AB∥CD,点E在直线AB与CD之间,连结AE、CE,试说明∠AEC=∠A+∠DCE.下面给出了这道题的解题过程,请将解题过程中的解题依据补充完整.
证明:如图2,过点E作EF∥AB,
∴∠A=∠1,( )
∵AB∥CD(已知),EF∥AB(辅助线作法),
∴EF∥CD,( )
∴∠2=∠DCE,( )
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠DCE;( )
(2)【探究】当点E在如图2的位置时,其他条件不变,试说明∠A+∠AEC+∠C=360°;
(3)【应用】如图,延长线段AE交直线CD于点M,已知∠A=130°,∠DCE=120°,求∠MEC的度数(请直接写出答案).
20.如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)求证:AD∥CE;
(2)若DA平分∠BDC,DA⊥FE于点A,∠FAB=55°,求∠ABD的度数.
参考答案
一.选择题
1.【解答】解:如图,
∵∠3和∠2是对顶角,
∴∠3=∠2=56°,
∵a∥b,
∴∠1=∠3=56°.
故选:D.
2.【解答】解:∵OP是∠AOB的平分线,∠AOB=30°,
∴∠POA=∠AOB=15°,
∵PC∥OA,
∴∠CPO=∠POA=15°.
故选:C.
3.【解答】解:∵∠1=38°,
∴∠3=90°﹣∠1=90°﹣38°=52°,
∵直尺的两边互相平行,
∴∠3=∠4=52°
∴∠2=180°﹣52°=128°,
故选:A.
4.【解答】解:如图,过点C作直线c∥a,则∠1=28°.
又∵a∥b,
∴c∥b,
∴∠2=45°,
∴∠ACD=28°+45°=73°.
故选:C.
5.【解答】解:如图,作EF∥AB,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠B+∠BEF=180°,∠C=∠CEF,
∵∠ABE=125°,∠C=30°,
∴∠BEF=55°,∠CEF=30°,
∴∠BEC=55°+30°=85°.
故选:D.
6.【解答】解:∵∠AEG=20°,∠GEF=45°,
∴∠AEF=∠AEG+∠GEF=20°+45°=65°.
∵AB∥CD,
∴∠DFE=∠AEF=65°,
∴∠HFD=∠DFE﹣∠EFH=65°﹣30°=35°.
故选:B.
7.【解答】解:A、是问句,未做判断,故本选项错误;
B、是祈使句,不符合命题的概念,故本选项错误;
C、是描述性语句,未做判断,故本选项错误;
D、符合命题的概念,故本选项正确;
故选:D.
8.【解答】解:A、两直线平行,同位角相等,故原命题错误,是假命题,不符合题意;
B、两直线平行,内错角相等,故原命题错误,是假命题,不符合题意;
C、相等的角不一定是对顶角,故原命题错误,是假命题,不符合题意;
D、同旁内角互补,两直线平行,正确,是真命题,符合题意.
故选:D.
二.填空题
9.【解答】解:“内错角相等,两直线平行”是真命题.
故答案为:真.
10.【解答】解:命题同角的补角相等写成“如果……,那么……”的形式:如果两个角是同角的补角,那么这两个角相等,
故答案为:如果两个角是同角的补角,那么这两个角相等.
11.【解答】解:∵AC∥EF,∠CAP=36°,
∴∠APE=∠CAP=36°,
∵BD∥EF,∠DBP=58°,
∴∠BPE=∠DBP=58°,
∴∠APB=∠APE+∠BPE=94°.
故答案为:94°.
12.【解答】解:∵∠AOD':∠D'OG=4:3,
设∠AOD'=4x,则∠D'OG=3x,
由翻折可知∠DOG=∠D'OG=3x∵∠AOD'+∠D'OG+∠DOG=180°,
即10x=180°,
解得x=18°,
∵AD∥BC,
∴∠BGO=∠DOG=3x=54°,
故答案为:54.
13.【解答】解:∵AB∥CD,
∴∠BEF+∠DFE=180°,
∵∠1+∠2=110°,
∴∠GEF+∠GFE=180°﹣110°=70°.
故答案为:70°.
14.【解答】解:①∵∠1=∠2,∴AB∥DC;故是真命题;
②∵∠4=∠5,∴AD∥BC;故是真命题;
③∵∠ABC+∠ACB+∠2=180°,∴AB∥CD;故是真命题;
④由∠3=∠ABD,不能判定AD∥BC,故是假命题;
故答案为:①②③.
三.解答题
15.【解答】解:∠A+∠D=180°.理由如下:
∵AB∥DE(已知),
∴∠A=∠DPC(两直线平行同位角相等),
∵AC∥DF(已知),
∴∠D+∠DPC=180° (两直线平行同旁内角互补),
∴∠A+∠D=180°(等量代换 ).
故答案为:已知,∠DPC,两直线平行同位角相等,已知,∠DPC,两直线平行同旁内角互补,等量代换.
16.【解答】解:∵∠3=∠4(已知),
∴AE∥BC(内错角相等,两直线平行),
∴∠EDC=∠5(两直线平行,内错角相等),
∵∠5=∠A(已知),
∴∠EDC=∠A(等量代换),
∴DC∥AB(同位角相等,两直线平行),
∴∠5+∠ABC=180°(两直线平行,同旁内角互补),
即∠5+∠2+∠3=180°,
∵∠1=∠2(已知),
∴∠5+∠1+∠3=180°(等量代换),
即∠BCF+∠3=180°,
∴BE∥CF(同旁内角互补,两直线平行).
故答案为:BC;内错角相等,两直线平行;两直线平行,内错角相等;∠A;同位角相等,两直线平行;两直线平行,同旁内角互补;等量代换;同旁内角互补,两直线平行.
17.【解答】(1)证明:∵∠2+∠BDC=180°,∠1+∠2=180°,
∴∠1=∠BDC,
∴EF∥AB;
(2)证明:∵EF∥AB,
∴∠DEF=∠BDE,
∵∠DEF=∠A,
∴∠BDE=∠A,
∴DE∥AC,
∴∠ACB=∠DEB.
18.【解答】(1)证明:∵AB∥CD,
∴∠AFC=∠DCF,
∵CF平分∠ACD,
∴∠AFC=∠ACF,
∴∠AFC=∠ACF,
又∵CE⊥CF,∠GAH+∠AFC=90°,
∴∠ECH=∠GAH,
∴AG∥CE;
(2)解:∵AB∥CD,
∴∠ECD=∠GAF=120°,
又∵CE⊥CF,
∴∠DCF=∠ECD﹣∠ECF=120°﹣90°=30°,
∴∠AFC=∠DCF=30°.
19.【解答】(1)证明:如图1,过点E作EF∥AB,
∴∠A=∠1(两直线平行,内错角相等),
∵AB∥CD(已知),
∵EF∥AB(辅助线作法),
∴CD∥EF(平行于同一直线的两条直线平行),
∴∠2=∠DCE(两直线平行,内错角相等),
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠DCE(等量代换),
故答案为:两直线平行,内错角相等;平行于同一直线的两条直线平行;两直线平行,内错角相等;等量代换;
(2)证明:过点E作EF∥AB,如图2所示:
∵AB∥CD,
∴EF∥CD,
∴∠A+∠AEF=180°,∠C+∠CEF=180°,
∴∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°;
(3)解:同(2)得:∠A+∠AEC+∠DCE=360°,
∴∠AEC=360°﹣∠A﹣∠DCE=360°﹣130°﹣120°=110°,
∴∠MEC=180°﹣∠AEC=180°﹣110°=70°.
20.【解答】(1)证明:∵∠1=∠BDC,
∴AB∥CD,
∴∠2=∠ADC,
∵∠2+∠3=180°,
∴∠ADC+∠3=180°,
∴AD∥CE;
(2)解:∵DA∥CE,DA⊥FE,
∴CE⊥AE于E,
∴∠CEF=90°,
由(1)知AD∥CE,
∴∠DAF=∠CEF=90°,
∴∠ADC=∠2=∠DAF﹣∠FAB,
∵∠FAB=55°,
∴∠ADC=35°,
∵DA平分∠BDC,∠1=∠BDC,
∴∠1=∠BDC=2∠ADC=70°
∴∠ABD=180°﹣70°=110°.
一.选择题
1.如图,两条平行线a,b被第三条直线c所截.若∠2=56°,则∠1的度数为( )
A.120° B.112° C.124° D.56°
2.如图,已知OP平分∠AOB,∠AOB=30°,PC∥OA,则∠CPO为( )
A.30° B.10° C.15° D.5°
3.把一块直尺与一块三角板如图放置,若∠1=38°,则∠2的度数是( )
A.128° B.138° C.142° D.152°
4.如图,已知a∥b,则∠ACD的度数是( )
A.45° B.60° C.73° D.90°
5.如图,AB∥CD,∠ABE=125°,∠C=30°,则∠α=( )
A.70° B.75° C.80° D.85°
6.如图,AB∥CD,一副三角尺按如图所示放置,∠AEG=20°,则∠HFD的度数为( )
A.40° B.35° C.30° D.25°
7.下列语句属于命题的是( )
A.你今天打卡了吗? B.请戴好口罩!
C.画出两条相等的线段 D.同位角相等
8.下列命题是真命题的是( )
A.同位角相等
B.内错角相等
C.相等的角是对顶角
D.同旁内角互补,两直线平行
二.填空题
9.命题“内错角相等,两直线平行”是 (填“真”或“假”)命题.
10.把下列命题改写成“如果……,那么……”的形式:同角的补角相等.改写成 .
11.生活中常见的探照灯、汽车大灯等灯具都是凹面镜.如图,从光源P点照射到凹面镜上的光线PA、PB等反射以后沿着与直线PF平行的方向射出,若∠CAP=36°,∠DBP=58°,则∠APB的度数为 .
12.如图,把一个长方形纸片沿OG折叠后,C,D两点分别落在C',D'两点处,若∠AOD':∠D'OG=4:3,则∠BGO= 度.
13.如图,AB∥CD,∠1+∠2=110°,则∠GEF+∠GFE= .
14.如图,给出下列命题:①∵∠1=∠2,∴AB∥DC; ②∵∠4=∠5,∴AD∥BC; ③∵∠ABC+∠ACB+∠2=180°,∴AB∥CD; ④∵∠3=∠ABD,∴AD∥BC,其中正确的命题有 .
三.解答题
15.如图,若AB∥DE,AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由.
解:∠A+∠D=180°.
理由如下:
∵AB∥DE( )
∴∠A= ( )
∵AC∥DF( )
∴∠D+ =180°( )
∴∠A+∠D=180°( )
16.如图,已知∠1=∠2,∠3=∠4,∠5=∠A,试说明:BE∥CF.
完善下面的解答过程,并填写理由或数学式:解:
∵∠3=∠4(已知)
∴AE∥ ( )
∴∠EDC=∠5( )
∵∠5=∠A(已知)
∴∠EDC= (等量代换)
∴DC∥AB( )
∴∠5+∠ABC=180°( )
即∠5+∠2+∠3=180°
∵∠1=∠2(已知)
∴∠5+∠1+∠3=180°( )
即∠BCF+∠3=180°
∴BE∥CF( ).
17.如图,已知∠1+∠2=180°,∠DEF=∠A,
求证:
(1)EF∥AB.
(2)∠ACB=∠DEB.
18.如图,AB∥CD,连结CA并延长至点H,CF平分∠ACD,CE⊥CF,∠GAH+∠AFC=90°.
(1)求证AG∥CE;
(2)若∠GAF=120°,求∠AFC的度数.
19.(1)【感知】如图1,AB∥CD,点E在直线AB与CD之间,连结AE、CE,试说明∠AEC=∠A+∠DCE.下面给出了这道题的解题过程,请将解题过程中的解题依据补充完整.
证明:如图2,过点E作EF∥AB,
∴∠A=∠1,( )
∵AB∥CD(已知),EF∥AB(辅助线作法),
∴EF∥CD,( )
∴∠2=∠DCE,( )
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠DCE;( )
(2)【探究】当点E在如图2的位置时,其他条件不变,试说明∠A+∠AEC+∠C=360°;
(3)【应用】如图,延长线段AE交直线CD于点M,已知∠A=130°,∠DCE=120°,求∠MEC的度数(请直接写出答案).
20.如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)求证:AD∥CE;
(2)若DA平分∠BDC,DA⊥FE于点A,∠FAB=55°,求∠ABD的度数.
参考答案
一.选择题
1.【解答】解:如图,
∵∠3和∠2是对顶角,
∴∠3=∠2=56°,
∵a∥b,
∴∠1=∠3=56°.
故选:D.
2.【解答】解:∵OP是∠AOB的平分线,∠AOB=30°,
∴∠POA=∠AOB=15°,
∵PC∥OA,
∴∠CPO=∠POA=15°.
故选:C.
3.【解答】解:∵∠1=38°,
∴∠3=90°﹣∠1=90°﹣38°=52°,
∵直尺的两边互相平行,
∴∠3=∠4=52°
∴∠2=180°﹣52°=128°,
故选:A.
4.【解答】解:如图,过点C作直线c∥a,则∠1=28°.
又∵a∥b,
∴c∥b,
∴∠2=45°,
∴∠ACD=28°+45°=73°.
故选:C.
5.【解答】解:如图,作EF∥AB,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠B+∠BEF=180°,∠C=∠CEF,
∵∠ABE=125°,∠C=30°,
∴∠BEF=55°,∠CEF=30°,
∴∠BEC=55°+30°=85°.
故选:D.
6.【解答】解:∵∠AEG=20°,∠GEF=45°,
∴∠AEF=∠AEG+∠GEF=20°+45°=65°.
∵AB∥CD,
∴∠DFE=∠AEF=65°,
∴∠HFD=∠DFE﹣∠EFH=65°﹣30°=35°.
故选:B.
7.【解答】解:A、是问句,未做判断,故本选项错误;
B、是祈使句,不符合命题的概念,故本选项错误;
C、是描述性语句,未做判断,故本选项错误;
D、符合命题的概念,故本选项正确;
故选:D.
8.【解答】解:A、两直线平行,同位角相等,故原命题错误,是假命题,不符合题意;
B、两直线平行,内错角相等,故原命题错误,是假命题,不符合题意;
C、相等的角不一定是对顶角,故原命题错误,是假命题,不符合题意;
D、同旁内角互补,两直线平行,正确,是真命题,符合题意.
故选:D.
二.填空题
9.【解答】解:“内错角相等,两直线平行”是真命题.
故答案为:真.
10.【解答】解:命题同角的补角相等写成“如果……,那么……”的形式:如果两个角是同角的补角,那么这两个角相等,
故答案为:如果两个角是同角的补角,那么这两个角相等.
11.【解答】解:∵AC∥EF,∠CAP=36°,
∴∠APE=∠CAP=36°,
∵BD∥EF,∠DBP=58°,
∴∠BPE=∠DBP=58°,
∴∠APB=∠APE+∠BPE=94°.
故答案为:94°.
12.【解答】解:∵∠AOD':∠D'OG=4:3,
设∠AOD'=4x,则∠D'OG=3x,
由翻折可知∠DOG=∠D'OG=3x∵∠AOD'+∠D'OG+∠DOG=180°,
即10x=180°,
解得x=18°,
∵AD∥BC,
∴∠BGO=∠DOG=3x=54°,
故答案为:54.
13.【解答】解:∵AB∥CD,
∴∠BEF+∠DFE=180°,
∵∠1+∠2=110°,
∴∠GEF+∠GFE=180°﹣110°=70°.
故答案为:70°.
14.【解答】解:①∵∠1=∠2,∴AB∥DC;故是真命题;
②∵∠4=∠5,∴AD∥BC;故是真命题;
③∵∠ABC+∠ACB+∠2=180°,∴AB∥CD;故是真命题;
④由∠3=∠ABD,不能判定AD∥BC,故是假命题;
故答案为:①②③.
三.解答题
15.【解答】解:∠A+∠D=180°.理由如下:
∵AB∥DE(已知),
∴∠A=∠DPC(两直线平行同位角相等),
∵AC∥DF(已知),
∴∠D+∠DPC=180° (两直线平行同旁内角互补),
∴∠A+∠D=180°(等量代换 ).
故答案为:已知,∠DPC,两直线平行同位角相等,已知,∠DPC,两直线平行同旁内角互补,等量代换.
16.【解答】解:∵∠3=∠4(已知),
∴AE∥BC(内错角相等,两直线平行),
∴∠EDC=∠5(两直线平行,内错角相等),
∵∠5=∠A(已知),
∴∠EDC=∠A(等量代换),
∴DC∥AB(同位角相等,两直线平行),
∴∠5+∠ABC=180°(两直线平行,同旁内角互补),
即∠5+∠2+∠3=180°,
∵∠1=∠2(已知),
∴∠5+∠1+∠3=180°(等量代换),
即∠BCF+∠3=180°,
∴BE∥CF(同旁内角互补,两直线平行).
故答案为:BC;内错角相等,两直线平行;两直线平行,内错角相等;∠A;同位角相等,两直线平行;两直线平行,同旁内角互补;等量代换;同旁内角互补,两直线平行.
17.【解答】(1)证明:∵∠2+∠BDC=180°,∠1+∠2=180°,
∴∠1=∠BDC,
∴EF∥AB;
(2)证明:∵EF∥AB,
∴∠DEF=∠BDE,
∵∠DEF=∠A,
∴∠BDE=∠A,
∴DE∥AC,
∴∠ACB=∠DEB.
18.【解答】(1)证明:∵AB∥CD,
∴∠AFC=∠DCF,
∵CF平分∠ACD,
∴∠AFC=∠ACF,
∴∠AFC=∠ACF,
又∵CE⊥CF,∠GAH+∠AFC=90°,
∴∠ECH=∠GAH,
∴AG∥CE;
(2)解:∵AB∥CD,
∴∠ECD=∠GAF=120°,
又∵CE⊥CF,
∴∠DCF=∠ECD﹣∠ECF=120°﹣90°=30°,
∴∠AFC=∠DCF=30°.
19.【解答】(1)证明:如图1,过点E作EF∥AB,
∴∠A=∠1(两直线平行,内错角相等),
∵AB∥CD(已知),
∵EF∥AB(辅助线作法),
∴CD∥EF(平行于同一直线的两条直线平行),
∴∠2=∠DCE(两直线平行,内错角相等),
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠DCE(等量代换),
故答案为:两直线平行,内错角相等;平行于同一直线的两条直线平行;两直线平行,内错角相等;等量代换;
(2)证明:过点E作EF∥AB,如图2所示:
∵AB∥CD,
∴EF∥CD,
∴∠A+∠AEF=180°,∠C+∠CEF=180°,
∴∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°;
(3)解:同(2)得:∠A+∠AEC+∠DCE=360°,
∴∠AEC=360°﹣∠A﹣∠DCE=360°﹣130°﹣120°=110°,
∴∠MEC=180°﹣∠AEC=180°﹣110°=70°.
20.【解答】(1)证明:∵∠1=∠BDC,
∴AB∥CD,
∴∠2=∠ADC,
∵∠2+∠3=180°,
∴∠ADC+∠3=180°,
∴AD∥CE;
(2)解:∵DA∥CE,DA⊥FE,
∴CE⊥AE于E,
∴∠CEF=90°,
由(1)知AD∥CE,
∴∠DAF=∠CEF=90°,
∴∠ADC=∠2=∠DAF﹣∠FAB,
∵∠FAB=55°,
∴∠ADC=35°,
∵DA平分∠BDC,∠1=∠BDC,
∴∠1=∠BDC=2∠ADC=70°
∴∠ABD=180°﹣70°=110°.
