沪科版七年级下册数学 6.2.2实数与数轴 课件(共16张PPT)
文档属性
| 名称 | 沪科版七年级下册数学 6.2.2实数与数轴 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 569.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
6.2 实数与数轴
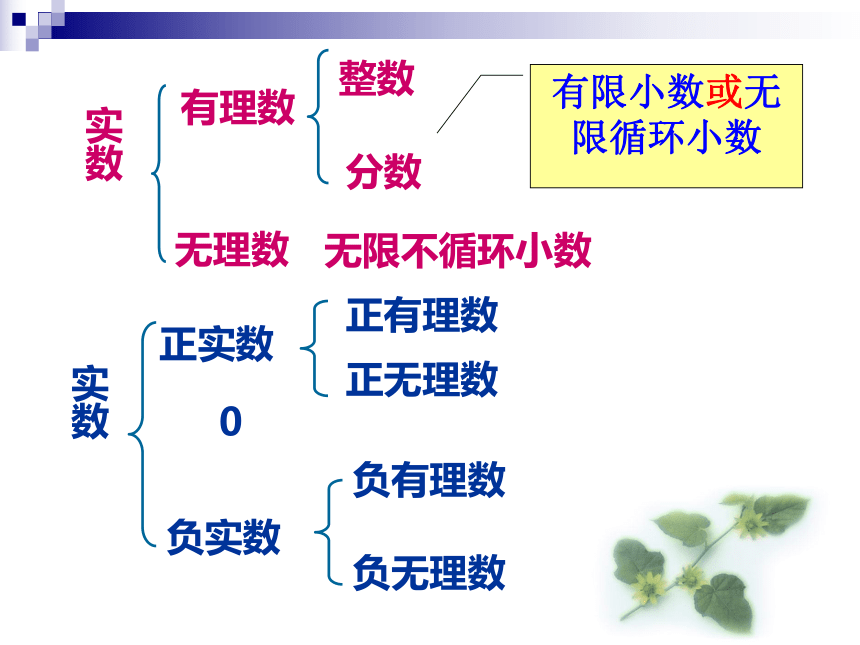
实数
实数
有理数
无理数
整数
分数
无限不循环小数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
有限小数或无限循环小数
把下列各数填入相应的集合内:
有理数集合:
无理数集合:
整数集合:
分数集合:
实数集合:
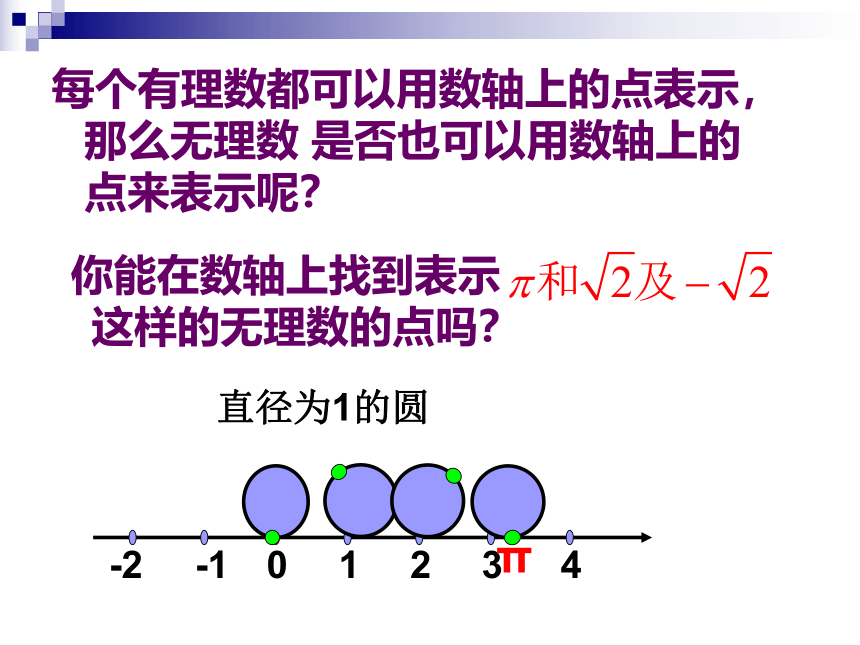
每个有理数都可以用数轴上的点表示,那么无理数 是否也可以用数轴上的点来表示呢?
你能在数轴上找到表示 这样的无理数的点吗?
0
1
2
4
3
-1
-2
π
直径为1的圆
0
1
2
4
3
-1
-2
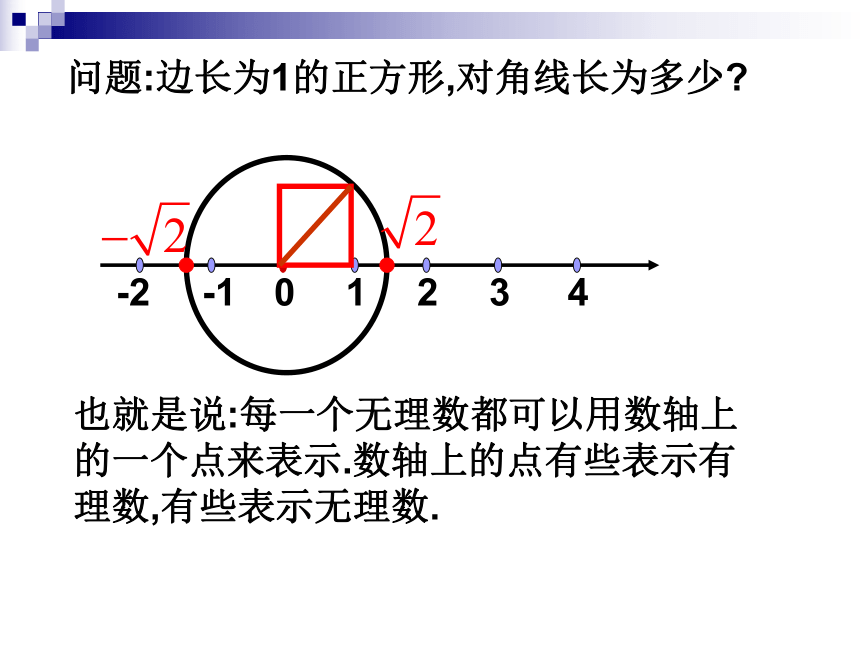
问题:边长为1的正方形,对角线长为多少
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
实数与数轴上的点是一一对应的.
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
实数的相反数、绝对值、倒数
相反数:
实数 a 的相反数是- a.若a与b互为相反数,则a+b=0.
绝对值:
实数a的绝对值,记为|a|,它是一个非负实数.
|a| =
a( a﹥0 )
0 ( a = 0)
-a( a﹤0)
几何意义: |a|表示点a到原点0的距离.而| a-b |表示点a与点b的距离.
倒数:
乘积是1的两个数互为倒数.若a与b互为倒数,则ab=1.
如果 a ≠ 0 ,那么它的倒数为 .
数轴上的右边点表示的数总是大于左边点表示的数,正数大于一切负数和零,零大于一切负数,两个负数比较绝对值大的反而小。
实数的比较大小
实数的运算
有理数的运算法则和运算律同样适用于实数。
的相反数是 ,
二计算:
绝对值是
例题:
。
一
(结果精确到0.01)
填空
2、 的相反数是 ,绝对值是 .
3、绝对值等于 的数是 , 的平方 是 .
4、比较大小:-7
1、正实数的绝对值是 ,0的绝对值是 ,负实数的绝对值是 .
它本身
0
它的相反数
一、判断:
1.实数不是有理数就是无理数。( )
2.无理数和数轴上的点一一对应(
3.两个无理数之积不一定是无理数。( )
4.两个无理数之和一定是无理数。( )
×
5.有理数与无理数之和一定是无理数 ( )
)
×
二.如图,数轴上表示1、 的对应点分别是A、
B,点B关于点A的对称点为C,则C点所表示
的数是( )
C
A
B
0
1
C
1、下列说法中错误的一个是( )
A、如果a、b 互为相反数,那么a+1和b-1仍是相反数;
B、不论x是什么实数,x -2x+ 的值 总是大于0;
C、若
2、1.7- 的相反数是 ,1.7- 的绝对值等于 .
3、设a、b是有理数,且满足a+ b=(1- ),求a 值。
能力训练:
则
1
4.实数a、b、c在数轴上的对应点如图所示,
其中点c是点a与点b的中点.
0
c
b
a
试化简:
解:
6.2 实数与数轴
实数
实数
有理数
无理数
整数
分数
无限不循环小数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
有限小数或无限循环小数
把下列各数填入相应的集合内:
有理数集合:
无理数集合:
整数集合:
分数集合:
实数集合:
每个有理数都可以用数轴上的点表示,那么无理数 是否也可以用数轴上的点来表示呢?
你能在数轴上找到表示 这样的无理数的点吗?
0
1
2
4
3
-1
-2
π
直径为1的圆
0
1
2
4
3
-1
-2
问题:边长为1的正方形,对角线长为多少
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
实数与数轴上的点是一一对应的.
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
实数的相反数、绝对值、倒数
相反数:
实数 a 的相反数是- a.若a与b互为相反数,则a+b=0.
绝对值:
实数a的绝对值,记为|a|,它是一个非负实数.
|a| =
a( a﹥0 )
0 ( a = 0)
-a( a﹤0)
几何意义: |a|表示点a到原点0的距离.而| a-b |表示点a与点b的距离.
倒数:
乘积是1的两个数互为倒数.若a与b互为倒数,则ab=1.
如果 a ≠ 0 ,那么它的倒数为 .
数轴上的右边点表示的数总是大于左边点表示的数,正数大于一切负数和零,零大于一切负数,两个负数比较绝对值大的反而小。
实数的比较大小
实数的运算
有理数的运算法则和运算律同样适用于实数。
的相反数是 ,
二计算:
绝对值是
例题:
。
一
(结果精确到0.01)
填空
2、 的相反数是 ,绝对值是 .
3、绝对值等于 的数是 , 的平方 是 .
4、比较大小:-7
1、正实数的绝对值是 ,0的绝对值是 ,负实数的绝对值是 .
它本身
0
它的相反数
一、判断:
1.实数不是有理数就是无理数。( )
2.无理数和数轴上的点一一对应(
3.两个无理数之积不一定是无理数。( )
4.两个无理数之和一定是无理数。( )
×
5.有理数与无理数之和一定是无理数 ( )
)
×
二.如图,数轴上表示1、 的对应点分别是A、
B,点B关于点A的对称点为C,则C点所表示
的数是( )
C
A
B
0
1
C
1、下列说法中错误的一个是( )
A、如果a、b 互为相反数,那么a+1和b-1仍是相反数;
B、不论x是什么实数,x -2x+ 的值 总是大于0;
C、若
2、1.7- 的相反数是 ,1.7- 的绝对值等于 .
3、设a、b是有理数,且满足a+ b=(1- ),求a 值。
能力训练:
则
1
4.实数a、b、c在数轴上的对应点如图所示,
其中点c是点a与点b的中点.
0
c
b
a
试化简:
解:
