沪科版七年级下册数学 7.2.3一元一次不等式的运用 课件(共15张PPT)
文档属性
| 名称 | 沪科版七年级下册数学 7.2.3一元一次不等式的运用 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 13:42:51 | ||
图片预览






文档简介
(共15张PPT)
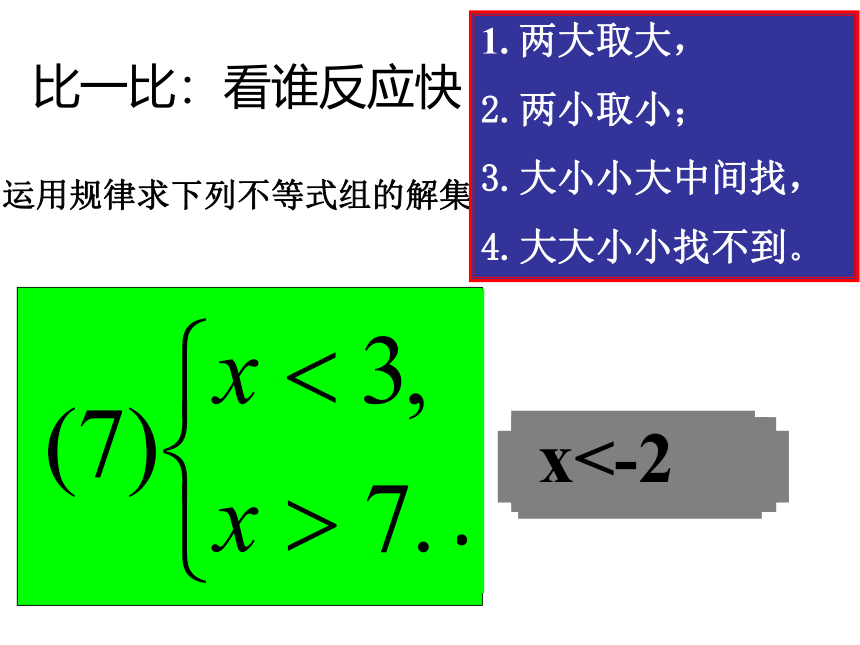
比一比:看谁反应快
运用规律求下列不等式组的解集:
1. 两大取大,
2.两小取小;
3.大小小大中间找,
4.大大小小找不到。
x>2
x>-2
x<3
x<-4
3-1无解
无解
-2≤x<1
x≤-2
x<-2
1、一本英语书共98页,张力读了一周(7天)还没读完,而李永不到一周就已读完。李永平均每天比张力多读3页,张力平均每天读多少页?(答案取整数)
张力7天读书的页数 < 98
李永7天读书的页数 > 98
不等关系:
解:设张力平均每天读 页,
由题中不等关系得:
①
②
由不等式①得:
由不等式②得:
根据题意,x 的值应是整数
答:张力平均每天读12或13页.
李永平均每天读( )页
2、在一次绿色环保知识竞赛中,共有20道题,对于每一道题,答对了得10分,答错或不答扣5分。已知小明得分在60到80分之间,那么小明答对了几道题?
60 小明得分
小明得分 80
不等关系:
go
解:设小明答对了 道,
由题中不等关系得:
①
②
由不等式①得:
由不等式②得:
答:小明答对了11或12道.
答错了 道
go
根据题意, 的值应是整数
应用一元一次不等式组解实际问题的一般步骤:
实际问题
(包含不等关系)
数学问题
(一元一次不等式组)
数学问题的解
(不等式组的解集)
实际问题的
解答
设未知数,列不等式
检验
解不等式组
抓关键语句
去括号
移项
合并
系数化为1
去分母
1、有若干学生参加夏令营活动,晚上在一宾馆住宿时,如果每间住4人,那么还有20人住不下,相同的房间,如果每间住8人,那么还有一间住不满也不空,请问:这群学生有多少人?有多少房间供他们住?
分析:由于一间房住不满也不空,所以该问题应该是建立不等式模型来解决.若设有x间房供他们住,则学生有(4x+20)人,住8人的房间有(x-1)间,另有一间住了学生但不足8人,这样我们就可得到不等式组
解:设房间有x间 4x+20<8x x>5 4x+20>8﹙x-1﹚ x<7 ∴5<x<7 ∵x是整数 ∴x=6 4x+20=44 房间有6间,人有44个
{
方法1
解:设房间有x间 4x+20-8(x-1)<8 x<7 4x+20-8(x-1)>0 x>5 ∴5<x<7 ∵x是整数 ∴x=6 4x+20=44 房间有6间,人有44个
{
方法2: 抓最后一个房间分析
2、某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品需要甲种原料9千克。乙种原料3千克;生产B种产品,需要甲种原料4千克,乙种原料10千克,请你根据要求,设计出A、B两种产品的生产主案。
填写下表(质量单位:千克)
A B 合 计
X件 (50-x)件
甲(360)
乙(290)
产品
原料
原料
所需
9x
4(50-x)
9x+4(50-x)
3x
10(50-x )
3x+10(50-x)
解: 设安排生产A种产品x件,则生产B种产品(50-x)件,根据题意列不等式组得:
9x+4(50-x)≤360
3x+10(50-x)≤ 290
解得:
{
x≤32
x≥30
因为,x是正整数,所以,x可取30、31、32.
当x=32时,50-x=18
当x=31时,50-x=19
当x=30时,50-x=20
答: 有三种设计方案:
方案一,生产A种产品30件,B种产品20件;
方案二,生产A种产品31件,B种产品19件;
方案三,生产A种产品32件,B种产品18件。
所以,不等式组的解集是 30≤x≤32
3、现计划把甲种货物1240吨和乙种货物880吨,用一列货车运往某地,已知这列货车挂有A,B两种不同规格的货车厢共40节.
如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨,每节B型车厢最多可装甲种货物25吨和乙种货物35吨,装货时按此要求安排A,B两种车厢的节数,共有几种安排方案
A B
甲种货物1240kg
乙种货物880kg
x
(40-x)
合计
35x
25(40-x)
35x+25(40-x)
15x
35(40-x)
15x+ 35(40-x)
列表分析:
35x+25(40-x)≥1240
15x+ 35(40-x)≥880
35x+25(40-x)≥1240
15x+ 35(40-x)≥880
解之得 24 ≤x≤26
因为是整数和,所以可取24,25,26
方案1: A型车厢24节; B型车厢16节
方案2: A型车厢25节; B型车厢15节
方案3: A型车厢26节; B型车厢14节
解:设A型车厢有x节,则
比一比:看谁反应快
运用规律求下列不等式组的解集:
1. 两大取大,
2.两小取小;
3.大小小大中间找,
4.大大小小找不到。
x>2
x>-2
x<3
x<-4
3
无解
-2≤x<1
x≤-2
x<-2
1、一本英语书共98页,张力读了一周(7天)还没读完,而李永不到一周就已读完。李永平均每天比张力多读3页,张力平均每天读多少页?(答案取整数)
张力7天读书的页数 < 98
李永7天读书的页数 > 98
不等关系:
解:设张力平均每天读 页,
由题中不等关系得:
①
②
由不等式①得:
由不等式②得:
根据题意,x 的值应是整数
答:张力平均每天读12或13页.
李永平均每天读( )页
2、在一次绿色环保知识竞赛中,共有20道题,对于每一道题,答对了得10分,答错或不答扣5分。已知小明得分在60到80分之间,那么小明答对了几道题?
60 小明得分
小明得分 80
不等关系:
go
解:设小明答对了 道,
由题中不等关系得:
①
②
由不等式①得:
由不等式②得:
答:小明答对了11或12道.
答错了 道
go
根据题意, 的值应是整数
应用一元一次不等式组解实际问题的一般步骤:
实际问题
(包含不等关系)
数学问题
(一元一次不等式组)
数学问题的解
(不等式组的解集)
实际问题的
解答
设未知数,列不等式
检验
解不等式组
抓关键语句
去括号
移项
合并
系数化为1
去分母
1、有若干学生参加夏令营活动,晚上在一宾馆住宿时,如果每间住4人,那么还有20人住不下,相同的房间,如果每间住8人,那么还有一间住不满也不空,请问:这群学生有多少人?有多少房间供他们住?
分析:由于一间房住不满也不空,所以该问题应该是建立不等式模型来解决.若设有x间房供他们住,则学生有(4x+20)人,住8人的房间有(x-1)间,另有一间住了学生但不足8人,这样我们就可得到不等式组
解:设房间有x间 4x+20<8x x>5 4x+20>8﹙x-1﹚ x<7 ∴5<x<7 ∵x是整数 ∴x=6 4x+20=44 房间有6间,人有44个
{
方法1
解:设房间有x间 4x+20-8(x-1)<8 x<7 4x+20-8(x-1)>0 x>5 ∴5<x<7 ∵x是整数 ∴x=6 4x+20=44 房间有6间,人有44个
{
方法2: 抓最后一个房间分析
2、某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品需要甲种原料9千克。乙种原料3千克;生产B种产品,需要甲种原料4千克,乙种原料10千克,请你根据要求,设计出A、B两种产品的生产主案。
填写下表(质量单位:千克)
A B 合 计
X件 (50-x)件
甲(360)
乙(290)
产品
原料
原料
所需
9x
4(50-x)
9x+4(50-x)
3x
10(50-x )
3x+10(50-x)
解: 设安排生产A种产品x件,则生产B种产品(50-x)件,根据题意列不等式组得:
9x+4(50-x)≤360
3x+10(50-x)≤ 290
解得:
{
x≤32
x≥30
因为,x是正整数,所以,x可取30、31、32.
当x=32时,50-x=18
当x=31时,50-x=19
当x=30时,50-x=20
答: 有三种设计方案:
方案一,生产A种产品30件,B种产品20件;
方案二,生产A种产品31件,B种产品19件;
方案三,生产A种产品32件,B种产品18件。
所以,不等式组的解集是 30≤x≤32
3、现计划把甲种货物1240吨和乙种货物880吨,用一列货车运往某地,已知这列货车挂有A,B两种不同规格的货车厢共40节.
如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨,每节B型车厢最多可装甲种货物25吨和乙种货物35吨,装货时按此要求安排A,B两种车厢的节数,共有几种安排方案
A B
甲种货物1240kg
乙种货物880kg
x
(40-x)
合计
35x
25(40-x)
35x+25(40-x)
15x
35(40-x)
15x+ 35(40-x)
列表分析:
35x+25(40-x)≥1240
15x+ 35(40-x)≥880
35x+25(40-x)≥1240
15x+ 35(40-x)≥880
解之得 24 ≤x≤26
因为是整数和,所以可取24,25,26
方案1: A型车厢24节; B型车厢16节
方案2: A型车厢25节; B型车厢15节
方案3: A型车厢26节; B型车厢14节
解:设A型车厢有x节,则
