沪科版七年级下册数学 7不等式与不等式组复习 课件(共20张PPT)
文档属性
| 名称 | 沪科版七年级下册数学 7不等式与不等式组复习 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 832.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
不等式与不等式组复习
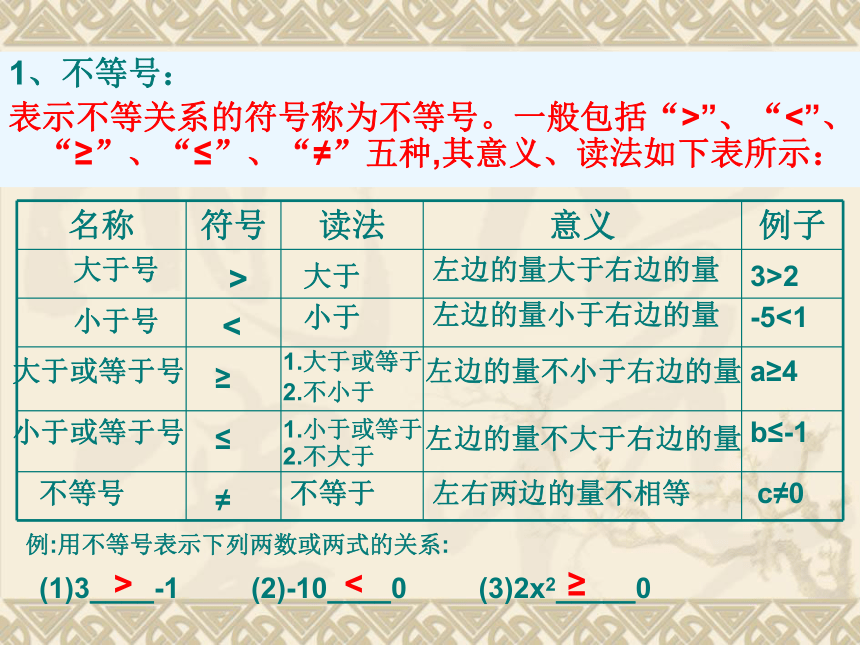
1、不等号:
表示不等关系的符号称为不等号。一般包括“>”、“<”、“≥”、“≤”、“≠”五种,其意义、读法如下表所示:
名称 符号 读法 意义 例子
大于号
>
大于
左边的量大于右边的量
3>2
小于号
<
小于
左边的量小于右边的量
-5<1
大于或等于号
1.大于或等于
2.不小于
左边的量不小于右边的量
a≥4
≤
≥
≠
小于或等于号
1.小于或等于
2.不大于
左边的量不大于右边的量
不等号
不等于
左右两边的量不相等
b≤-1
c≠0
例:用不等号表示下列两数或两式的关系:
(1)3____-1 (2)-10____0 (3)2x2_____0
>
<
≥
知识点2.
不等式:用不等号连接起来的式子.
用适当的符号表示下列关系:
(1)a的2倍比8小
(2)y的3倍与1的和大于3
(3)x除以2的商加2至多为5
(4)a与b两数和的平方不大于2
(5)x与y的差为非正数
(6)a与4的和不小于2
2a<8
3y+1>3
(a+b)2≤2
X-y≤0
a+4≥2
3.不等式的基本性质:
性质1:不等式的两边加(或减)同一个数(或式子),不等号方向不变。即如果a>b,那么a±c>b±c.
性质2:不等式的两边乘以(或除以)同一个正数,不等号的方向不变。即如果a>b,c>0,那么ac>bc,a/c>b/c.
性质 3:不等式的两边乘以(或除以)同一个负数,不等号的方向改变。即如果a>b,c<0,那么ac<bc,a/c<b/c.
例:
由aA.m>0 B.m<0 C.m≤0 D.m≥0.
注:在不等式两边都乘以(或除以)同一个数(式子)时,应考虑正数、负数、零三种情况。
4、不等式的解:
使不等式成立的未知数的值.
例:-2是不是不等式2x-1>-3的解?4呢?
解:当X=-2时,2x-1=2×(-2)-1=5<-3,即不等式左边<右边,所以x=-2不是不等式2x-1>-3.的解.当x=4时,2x-1=2×4-1=7>-3,即不等式左边>右边,所以x=4是不等式2x-1>-3的解.
5、不等式的解集:
一个含有未知数的不等式的所有解,组成了这个不等式的解集。
例:x<5是不等式3x-5<2x的解集,则下列说法正确的有( )个。
①5是不等式3x-5<2x的一个解;②0是不等式3x-5<2x的一个解;③x<4也是不等式3x-5<2x的解集;④所有小于4的数都是不等式3x-5<2x的解。
分析:x<5是不等式3x-5<2x的解集,说明任何一个小于5的数都是不等式3x-5<2x的一个解,当然小于4的值也一定是不等式3x-5<2x的解,但x<4不是不等式的解集,因为它不是由不等式的所有解组成的。
A.1个; B.2个; C.3个; D.4个.
B
6、解不等式:
求不等式解集的过程
其实质就是把不等式化为“x>a或x≥a或x7、数轴表示不等式解集:
x>a
xx≥a
x≤a
a
a
a
a
大向右,小向左,注意空实心
例:
1.关于x的不等式2x-a≤-1的解集如图所示,则a的取值是( )
A.0; B.-3; C.-2; D.-1
0
-1
-2
-3
-4
1
2
3
2.如图,表示的是不等式的解集,或中错误的是( )
0
1
-1
-2
x≥-1
0
-2
1
2
-1
x<1
0
-2
1
2
-1
x≥0
0
-2
1
2
-1
x>0
A
B
C
D
用数轴表示不等式的步骤:(1)画数轴;(2)定界点;(3)定方向.
8、不等式解集中最值问题:
对于不等式x≥a的解集有最小值,最小值为x=a;对于不等式x≤a的解集有最大值,最大值为x=a,而不等式x>a的解集没有最小值,x例:x≥2时x的最小值是a,x≤5时x的最大值是b,试求ba的值。
解:根据已知条件,得a=2,b=5则ba=52=25
9、一元一次不等式:
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式。
解一元一次不等式步骤:
去分母 去括号 移项 合并同类项
系数化为1.
在系数化为1的这一步中,要特别注意不等式的两边都乘以(或除以)一个负数时,不等号的方向必须改变方向.
10、一元一次不等式的解法
2 求不等式 3x+1≥4x-5的正整数解.
8x-4≥15x-60
8x-15x≥-60+4
-7x≥-56
x≤8
去分母得:
去括号得:
移项得:
合并同类项得:
化系数为1得:
解:
同乘最简公分母12,方向不变
同除以-7,方向改变
0
1
2
-1
3
4
5
6
7
8
2求不等式 3x+1≥4x-5的正整数解.
移项得:
合并同类项得:
化系数为1得:
解:
3x﹣4x≥-5-1
﹣x ≥-6
x≤6
所以不等式 的正整数解为:1、2、3、4、5、6
解:由 ,得
3 若关于x的方程 的解是非负数,求m的取值范围。
13、一元一次不等式组:
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组。
14、一元一次不等式组的解集:
一般地,一元一次不等式组中各个不等式解集的公共部分,叫这个一元一次不等式组的解集。
15、一元一次不等式组的解集的取法:
最简不等式组(ax>a
x>b
xxx>a
xxx>b
a
b
a
b
a
b
a
b
x>b
xa无解
同大取大
同小取小
大小小大取中间
大大小小解不了
16、一元一次不等式组的解法:
步骤:
(1)先分别解不等式组中的每一个不等式,分别求出它们的解集;
(2)将每个不等式的解集在同一条数轴上表示出来,找出它们的公共部分,注意:公共部分可能没有,也可能是一个点;
(3)根据公共部分写出不等式组的解集,若没有公共部分,则说明不等式组无解。
特别注意:用数轴表示不等式的解集时,<、>用空心,≤、≥用实心。 >、≥向右画,<、≤向左画。
2.求不等式组 的整数解.
1.解不等式组
3.一个三角形三边长分别为3、1-2a、8,求a
的范围?
1:解不等式组:
由不等式①得: x≤8
由不等式②得: x≥5
∴ 原不等式组的解集为:5≤x≤8
解:
0
1
2
-1
3
4
5
6
7
8
①
②
2.求不等式组 的整数解.
解:
0
4
由不等式①得: x>2
由不等式②得: x≤4
∴ 不等式组的解集为:2<x≤4
1
2
-1
3
5
6
7
8
不等式组的整数解为:3、4
①
②
不等式(组)在实际生活中的应用
当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属列不等式(组)来解决的问题,而不能列方程(组)来解.
列一元一次不等式组解应用题的一般步骤:
1、审:审清题意,弄懂已知什么,求什么,以及各个数量之间的关系。
2、设:只能设一个未知数,一般是与所求问题有直接关系的量。
3、找:找出题中所有的不等关系,特别是隐含的数量关系。
4、列:列出不等式组。
5、解:分别解出每个不等式的解集,再求其公共部分,得出结果。
6、答:根据所得结果作出回答。
例、某饮料厂为了开发新产品,用A、B两种果汁原料各19千克、17.2千克试制甲、乙两种新型饮料共50千克,下表是相关数据:
每千克会含量
饮料
A(单位:千克)
B(单位:千克)
甲
乙
0.5
0.2
0.3
0.4
(1)假设甲种饮料需配制x千克,请你写出满足题意的不等式组,并求出其解集.
(2)若甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,设这两种饮料的成本总额为y元,请写出y与x的函数关系式(不要求写自变量的取值范围),并根据(1)的运算结果,确定当甲种饮料配制多少千克时,甲、乙两种饮料的成本总额最少?
解:(1)由题意得:
解不等式组,得
(2)y=4x+3(50-x),即y=x+150。因为x越小,y越小,所以当x=28时,y最小。即当甲种饮料配制28千克时,甲、乙两种饮料的成本总额最少。
0.5x+0.2(50-x) ≤19
0.3x+0.4(50-x) ≤17.2
28≤x≤30
不等式与不等式组复习
1、不等号:
表示不等关系的符号称为不等号。一般包括“>”、“<”、“≥”、“≤”、“≠”五种,其意义、读法如下表所示:
名称 符号 读法 意义 例子
大于号
>
大于
左边的量大于右边的量
3>2
小于号
<
小于
左边的量小于右边的量
-5<1
大于或等于号
1.大于或等于
2.不小于
左边的量不小于右边的量
a≥4
≤
≥
≠
小于或等于号
1.小于或等于
2.不大于
左边的量不大于右边的量
不等号
不等于
左右两边的量不相等
b≤-1
c≠0
例:用不等号表示下列两数或两式的关系:
(1)3____-1 (2)-10____0 (3)2x2_____0
>
<
≥
知识点2.
不等式:用不等号连接起来的式子.
用适当的符号表示下列关系:
(1)a的2倍比8小
(2)y的3倍与1的和大于3
(3)x除以2的商加2至多为5
(4)a与b两数和的平方不大于2
(5)x与y的差为非正数
(6)a与4的和不小于2
2a<8
3y+1>3
(a+b)2≤2
X-y≤0
a+4≥2
3.不等式的基本性质:
性质1:不等式的两边加(或减)同一个数(或式子),不等号方向不变。即如果a>b,那么a±c>b±c.
性质2:不等式的两边乘以(或除以)同一个正数,不等号的方向不变。即如果a>b,c>0,那么ac>bc,a/c>b/c.
性质 3:不等式的两边乘以(或除以)同一个负数,不等号的方向改变。即如果a>b,c<0,那么ac<bc,a/c<b/c.
例:
由a
注:在不等式两边都乘以(或除以)同一个数(式子)时,应考虑正数、负数、零三种情况。
4、不等式的解:
使不等式成立的未知数的值.
例:-2是不是不等式2x-1>-3的解?4呢?
解:当X=-2时,2x-1=2×(-2)-1=5<-3,即不等式左边<右边,所以x=-2不是不等式2x-1>-3.的解.当x=4时,2x-1=2×4-1=7>-3,即不等式左边>右边,所以x=4是不等式2x-1>-3的解.
5、不等式的解集:
一个含有未知数的不等式的所有解,组成了这个不等式的解集。
例:x<5是不等式3x-5<2x的解集,则下列说法正确的有( )个。
①5是不等式3x-5<2x的一个解;②0是不等式3x-5<2x的一个解;③x<4也是不等式3x-5<2x的解集;④所有小于4的数都是不等式3x-5<2x的解。
分析:x<5是不等式3x-5<2x的解集,说明任何一个小于5的数都是不等式3x-5<2x的一个解,当然小于4的值也一定是不等式3x-5<2x的解,但x<4不是不等式的解集,因为它不是由不等式的所有解组成的。
A.1个; B.2个; C.3个; D.4个.
B
6、解不等式:
求不等式解集的过程
其实质就是把不等式化为“x>a或x≥a或x
x>a
x
x≤a
a
a
a
a
大向右,小向左,注意空实心
例:
1.关于x的不等式2x-a≤-1的解集如图所示,则a的取值是( )
A.0; B.-3; C.-2; D.-1
0
-1
-2
-3
-4
1
2
3
2.如图,表示的是不等式的解集,或中错误的是( )
0
1
-1
-2
x≥-1
0
-2
1
2
-1
x<1
0
-2
1
2
-1
x≥0
0
-2
1
2
-1
x>0
A
B
C
D
用数轴表示不等式的步骤:(1)画数轴;(2)定界点;(3)定方向.
8、不等式解集中最值问题:
对于不等式x≥a的解集有最小值,最小值为x=a;对于不等式x≤a的解集有最大值,最大值为x=a,而不等式x>a的解集没有最小值,x
解:根据已知条件,得a=2,b=5则ba=52=25
9、一元一次不等式:
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式。
解一元一次不等式步骤:
去分母 去括号 移项 合并同类项
系数化为1.
在系数化为1的这一步中,要特别注意不等式的两边都乘以(或除以)一个负数时,不等号的方向必须改变方向.
10、一元一次不等式的解法
2 求不等式 3x+1≥4x-5的正整数解.
8x-4≥15x-60
8x-15x≥-60+4
-7x≥-56
x≤8
去分母得:
去括号得:
移项得:
合并同类项得:
化系数为1得:
解:
同乘最简公分母12,方向不变
同除以-7,方向改变
0
1
2
-1
3
4
5
6
7
8
2求不等式 3x+1≥4x-5的正整数解.
移项得:
合并同类项得:
化系数为1得:
解:
3x﹣4x≥-5-1
﹣x ≥-6
x≤6
所以不等式 的正整数解为:1、2、3、4、5、6
解:由 ,得
3 若关于x的方程 的解是非负数,求m的取值范围。
13、一元一次不等式组:
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组。
14、一元一次不等式组的解集:
一般地,一元一次不等式组中各个不等式解集的公共部分,叫这个一元一次不等式组的解集。
15、一元一次不等式组的解集的取法:
最简不等式组(a
x>b
x
x
a
b
a
b
a
b
a
b
x>b
x
同大取大
同小取小
大小小大取中间
大大小小解不了
16、一元一次不等式组的解法:
步骤:
(1)先分别解不等式组中的每一个不等式,分别求出它们的解集;
(2)将每个不等式的解集在同一条数轴上表示出来,找出它们的公共部分,注意:公共部分可能没有,也可能是一个点;
(3)根据公共部分写出不等式组的解集,若没有公共部分,则说明不等式组无解。
特别注意:用数轴表示不等式的解集时,<、>用空心,≤、≥用实心。 >、≥向右画,<、≤向左画。
2.求不等式组 的整数解.
1.解不等式组
3.一个三角形三边长分别为3、1-2a、8,求a
的范围?
1:解不等式组:
由不等式①得: x≤8
由不等式②得: x≥5
∴ 原不等式组的解集为:5≤x≤8
解:
0
1
2
-1
3
4
5
6
7
8
①
②
2.求不等式组 的整数解.
解:
0
4
由不等式①得: x>2
由不等式②得: x≤4
∴ 不等式组的解集为:2<x≤4
1
2
-1
3
5
6
7
8
不等式组的整数解为:3、4
①
②
不等式(组)在实际生活中的应用
当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属列不等式(组)来解决的问题,而不能列方程(组)来解.
列一元一次不等式组解应用题的一般步骤:
1、审:审清题意,弄懂已知什么,求什么,以及各个数量之间的关系。
2、设:只能设一个未知数,一般是与所求问题有直接关系的量。
3、找:找出题中所有的不等关系,特别是隐含的数量关系。
4、列:列出不等式组。
5、解:分别解出每个不等式的解集,再求其公共部分,得出结果。
6、答:根据所得结果作出回答。
例、某饮料厂为了开发新产品,用A、B两种果汁原料各19千克、17.2千克试制甲、乙两种新型饮料共50千克,下表是相关数据:
每千克会含量
饮料
A(单位:千克)
B(单位:千克)
甲
乙
0.5
0.2
0.3
0.4
(1)假设甲种饮料需配制x千克,请你写出满足题意的不等式组,并求出其解集.
(2)若甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,设这两种饮料的成本总额为y元,请写出y与x的函数关系式(不要求写自变量的取值范围),并根据(1)的运算结果,确定当甲种饮料配制多少千克时,甲、乙两种饮料的成本总额最少?
解:(1)由题意得:
解不等式组,得
(2)y=4x+3(50-x),即y=x+150。因为x越小,y越小,所以当x=28时,y最小。即当甲种饮料配制28千克时,甲、乙两种饮料的成本总额最少。
0.5x+0.2(50-x) ≤19
0.3x+0.4(50-x) ≤17.2
28≤x≤30
