沪科版七年级下册数学 8.2.2单项式除以单项式 课件(共22张PPT)
文档属性
| 名称 | 沪科版七年级下册数学 8.2.2单项式除以单项式 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 13:52:38 | ||
图片预览







文档简介
(共22张PPT)
下雨时,常常是“先见闪电、后闻雷鸣”,这是因为光速比声速快的缘故。已知光在空气中的传播速度为3×108m/s ,而声音在空气中的传播速度约3× m/s,你知道光速是声速的多少倍吗?
学习了今天的知识,我们就能解决这个问题了!
复习提问
用字母表示幂的运算性质:
(1)am·an=am+n (m、n均为正整数)
(2)(am)n=amn (m、n均为正整数)
(3) (ab)n= anbn (n为正整数)
(4)am ÷ an= am-n (a≠0,m、n均为正整数,m>n)
(5)a0 =1(a≠0)
( 6 ) (a≠0,p是正整数)
试着填一填
8x3 · 5x2y=( )
40x5y
40x5y÷5x2y=( )
8x3
4a2x3·3ab2=( )
12a3b2x3÷3ab2=( )
被除式÷除式=商式
12a3b2x3
4a2x3
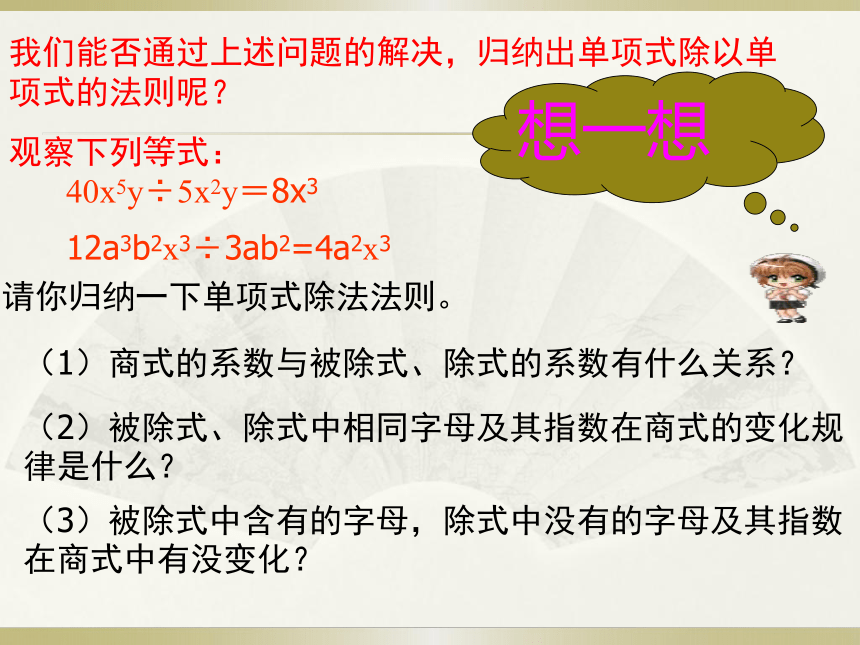
我们能否通过上述问题的解决,归纳出单项式除以单项式的法则呢?
观察下列等式:
40x5y÷5x2y=8x3
12a3b2x3÷3ab2=4a2x3
请你归纳一下单项式除法法则。
(1)商式的系数与被除式、除式的系数有什么关系?
(2)被除式、除式中相同字母及其指数在商式的变化规律是什么?
(3)被除式中含有的字母,除式中没有的字母及其指数在商式中有没变化?
想一想
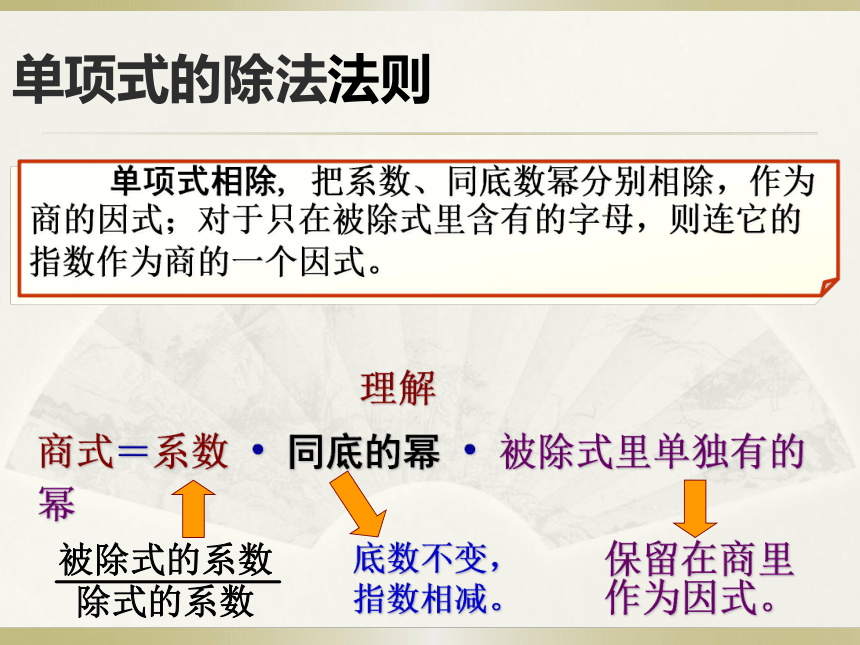
单项式的除法法则
单项式相除, 把系数、同底数幂分别相除,作为
商的因式;对于只在被除式里含有的字母,则连它的
指数作为商的一个因式。
理解
商式=系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减。
保留在商里
作为因式。
单项式相乘 单项式相除
第一步
第二步
第三步
系数相乘
系数相除
同底数幂相乘
同底数幂相除
其余字母不变连同其指数作为积的因式
只在被除式里含有的字母连同其指数一起作为商的因式
例1 计算
(1)28x4y2÷7x3y
解:
(1)28x4y2÷7x3y
=(28 ÷7)·x4-3y2-1
=4xy
(2)-5a5 b3c ÷15a4b
(2)-5a5 b3c ÷15a4b3
=[(-5)÷15]a5-4b3-3c
=- ac
下雨时,常常是“先见闪电、后闻雷鸣”,这是因为光速比声速快的缘故。已知光在空气中的传播速度为 ,而声音在空气中的传播速度约为 ,你知道光速是声速的多少倍吗?
3.0×108米/秒
3×102米/秒
解:
答:光速大约是声速的1000000倍,即100万倍。
巩固练习
分析:
此例题是单项式除以单项式,按照单项式除以单项式的法则计算就可以了.
第一阶梯
解:
计算
(1)(2.2×1011)÷(4.4×109)
(2)36x4y3z÷(5x2y)2
解:
计算:
(1)(5ab2c)4÷(-5ab2c2)2
解:
(1)(5ab2c)4÷(-5ab2c2)2
=(54a4b8c4)÷(52a2b4c4)
=54-2a4-2b8-4c4-4
=52a2b4c0
=25a2b4
说明: 当被除式的字母的指数与除式相同字母的指数相等时,可用a0=1省掉这个字母,用1相乘.
第二阶梯
第三阶梯
计算.
(1)(-3.6×1010)÷(-2×102)2÷(3×102)2
解:
(1)(-3.6×1010)÷(-2×102)2÷(3×102)2
=(-3.6×1010)÷(4×104)÷(9×104)
=-0.9×106÷(9×104)
=-0.1×102
=-10
说明: ①在有乘方、乘除综合运算中,先乘方然后从左到右按顺序相乘除. ②当除式的系数是负数时,一定要加上括号.③最后商式能应用多项式的乘法展开的,应该乘开.
解:
(4) (2ab)2·(a2-b2)-(2a2b2)2÷4b2+4a2b4
(2ab)2·(a2-b2)-(2a2b2)2÷4b2+4a2b4 =4a2b2(a2-b2)-4a4b4÷4b2+4a2b4 =4a4b2-4a2b4-a4b2+4a2b4 =3a4b2
解:
说明
在整式加减乘除、乘方运算中,应按运算顺序先乘方再乘除最后加减,有括号先算括号里面的,结果有同类项应合并。
思维拓展
1、系数?
2、同底数幂?
3、只在被除式里的幂?
单项式相除
相除
相除
不变
下雨时,常常是“先见闪电、后闻雷鸣”,这是因为光速比声速快的缘故。已知光在空气中的传播速度为3×108m/s ,而声音在空气中的传播速度约3× m/s,你知道光速是声速的多少倍吗?
学习了今天的知识,我们就能解决这个问题了!
复习提问
用字母表示幂的运算性质:
(1)am·an=am+n (m、n均为正整数)
(2)(am)n=amn (m、n均为正整数)
(3) (ab)n= anbn (n为正整数)
(4)am ÷ an= am-n (a≠0,m、n均为正整数,m>n)
(5)a0 =1(a≠0)
( 6 ) (a≠0,p是正整数)
试着填一填
8x3 · 5x2y=( )
40x5y
40x5y÷5x2y=( )
8x3
4a2x3·3ab2=( )
12a3b2x3÷3ab2=( )
被除式÷除式=商式
12a3b2x3
4a2x3
我们能否通过上述问题的解决,归纳出单项式除以单项式的法则呢?
观察下列等式:
40x5y÷5x2y=8x3
12a3b2x3÷3ab2=4a2x3
请你归纳一下单项式除法法则。
(1)商式的系数与被除式、除式的系数有什么关系?
(2)被除式、除式中相同字母及其指数在商式的变化规律是什么?
(3)被除式中含有的字母,除式中没有的字母及其指数在商式中有没变化?
想一想
单项式的除法法则
单项式相除, 把系数、同底数幂分别相除,作为
商的因式;对于只在被除式里含有的字母,则连它的
指数作为商的一个因式。
理解
商式=系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减。
保留在商里
作为因式。
单项式相乘 单项式相除
第一步
第二步
第三步
系数相乘
系数相除
同底数幂相乘
同底数幂相除
其余字母不变连同其指数作为积的因式
只在被除式里含有的字母连同其指数一起作为商的因式
例1 计算
(1)28x4y2÷7x3y
解:
(1)28x4y2÷7x3y
=(28 ÷7)·x4-3y2-1
=4xy
(2)-5a5 b3c ÷15a4b
(2)-5a5 b3c ÷15a4b3
=[(-5)÷15]a5-4b3-3c
=- ac
下雨时,常常是“先见闪电、后闻雷鸣”,这是因为光速比声速快的缘故。已知光在空气中的传播速度为 ,而声音在空气中的传播速度约为 ,你知道光速是声速的多少倍吗?
3.0×108米/秒
3×102米/秒
解:
答:光速大约是声速的1000000倍,即100万倍。
巩固练习
分析:
此例题是单项式除以单项式,按照单项式除以单项式的法则计算就可以了.
第一阶梯
解:
计算
(1)(2.2×1011)÷(4.4×109)
(2)36x4y3z÷(5x2y)2
解:
计算:
(1)(5ab2c)4÷(-5ab2c2)2
解:
(1)(5ab2c)4÷(-5ab2c2)2
=(54a4b8c4)÷(52a2b4c4)
=54-2a4-2b8-4c4-4
=52a2b4c0
=25a2b4
说明: 当被除式的字母的指数与除式相同字母的指数相等时,可用a0=1省掉这个字母,用1相乘.
第二阶梯
第三阶梯
计算.
(1)(-3.6×1010)÷(-2×102)2÷(3×102)2
解:
(1)(-3.6×1010)÷(-2×102)2÷(3×102)2
=(-3.6×1010)÷(4×104)÷(9×104)
=-0.9×106÷(9×104)
=-0.1×102
=-10
说明: ①在有乘方、乘除综合运算中,先乘方然后从左到右按顺序相乘除. ②当除式的系数是负数时,一定要加上括号.③最后商式能应用多项式的乘法展开的,应该乘开.
解:
(4) (2ab)2·(a2-b2)-(2a2b2)2÷4b2+4a2b4
(2ab)2·(a2-b2)-(2a2b2)2÷4b2+4a2b4 =4a2b2(a2-b2)-4a4b4÷4b2+4a2b4 =4a4b2-4a2b4-a4b2+4a2b4 =3a4b2
解:
说明
在整式加减乘除、乘方运算中,应按运算顺序先乘方再乘除最后加减,有括号先算括号里面的,结果有同类项应合并。
思维拓展
1、系数?
2、同底数幂?
3、只在被除式里的幂?
单项式相除
相除
相除
不变
