沪科版七年级下册数学 8.1.3同底数幂的除法 课件(共15张PPT)
文档属性
| 名称 | 沪科版七年级下册数学 8.1.3同底数幂的除法 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
同底数幂的除法(1)
1、同底数幂的乘法法则:
am · an=am+n(m、n都是正整数)
3、积的乘方法则:
2、幂的乘方法则:
(am)n=amn (m、n都是正整数)
(ab)n=anbn (n为正整数)
温故新知
① b3·b4· b = ( )
②(-a3)3 = ( )
b8
-a9
同底数幂相乘
幂的乘方
积的乘方
计算并说出它们分别是属于哪一种幂的运算.
③ = ( )
问题 一种数码照片的文件大小是27 KB,一个存储量为216 KB的移动存储器能存储多少张这样的数码照片?
分析:这个移动存储器的容量为216 KB,
它能存储这种数码照片的数量为
解:
探究与思考
观察计算结果,你能发现什么规律吗?
= 35-2
= 46-3
用你熟悉的方法填写课本P50表格
猜想:
m-n
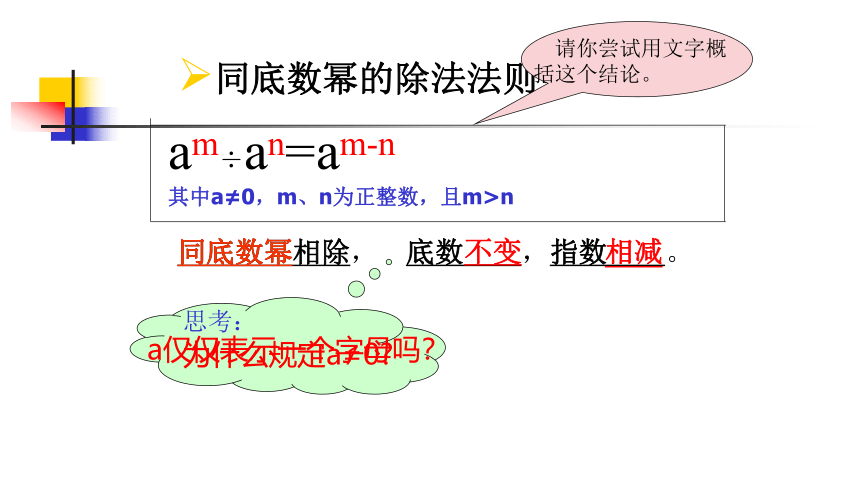
am÷an=am-n 其中a≠0,m、n为正整数,且m>n
同底数幂相除,
底数 ,指数 。
不变
相减
同底数幂的除法法则:
请你尝试用文字概括这个结论。
同底数幂
思考:
为什么规定a≠0
a仅仅表示一个字母吗?
理解与应用1
例1:计算
(1) a8÷a3 ; (2)(-a)10÷(-a)3;
( 3)(2a)7÷(2a)4 ; (4)x11÷(-x)5
⑵(-a)10÷(-a)3
解 ⑴ a8÷a3
= a8-3
= a5
= (-a)10-3
= (-a)7
= -a7
⑶(2a)7÷(2a)4
= (2a)7-4
= (2a)3
= 8a3
⑷ x11÷(-x)5
= x11÷(-x 5 )
= - x11÷x5
= - x6
下面的计算对不对?如果不对,怎样改正?
① a10 ÷ a2= a5( ) ② x5 ÷ x4 = x ( )
③a3 ÷a = a3 ( ) ④ (-b)4 ÷ (-b)2 = -b2 ( )
⑤ ( ) ⑥ ( )
a10 ÷ a2= a8
a3 ÷a = a2
(-b)4 ÷ (-b)2 =b2
×
√
×
×
×
×
想一想
比一比,看谁算的快!
题目
答案
巩固练习
例2:计算
(1) a10÷ a5 ÷ a2 (2)(x-1)5÷(1-x)2
解: (1)a10÷a5÷ a2
= a5÷a2
= a3
(2)(x-1)5÷(1-x)2
=(x-1)5÷(x -1)2
=(x-1)3
= -(1-x)5÷(1-x)2
=-(1-x)3
理解与应用2
巩固训练
计算:
(1) a10÷( a5 ÷ a2) (2)(a-b)4÷(b-a)2
(3)(a5) 2 · a3 ÷ (a2)3
1.如果x2m-1 ÷ x2 =xm+1,求m的值.
2. 若10m=16,10n=20,求10m-n的值.
解:∵ x2m-1 ÷ x2 =xm+1 ,
∴ ,
∴ 2m-1-2=m+1,
解得:m=4.
解:∵ 10m =16,10n=20,
∴ 10m-n =10m ÷ 10n =16 ÷ 20=0.8
变式训练
拓展练习
(1)若3x-2y-3=0,则103x÷102y= 。
(2)若xm=6,xn=2,则xm-n = ,
x2m-n = 。
(3)若10m=200,10n=2,则9m÷32 n= 。
1000
3
18
81
归纳小结
1、同底数幂的除法法则:同底数幂相除,底数不变,指数相减。
am÷an = am-n (a≠0,m,n都是正整数,且 m>n)
底数a可以代表一个数、字母、代数式等。
2、计算时的几个注意点:
(1)同底数幂的除法计算,直接应用法则,底数不变,指数相减;
(2)不是同底数幂时,应先化成同底数幂,再计算,注意符号;
(3)当底数是代数式时,应把这个代数式看成一个整体;
(4)混合运算时注意运算的顺序。
同底数幂的除法(1)
1、同底数幂的乘法法则:
am · an=am+n(m、n都是正整数)
3、积的乘方法则:
2、幂的乘方法则:
(am)n=amn (m、n都是正整数)
(ab)n=anbn (n为正整数)
温故新知
① b3·b4· b = ( )
②(-a3)3 = ( )
b8
-a9
同底数幂相乘
幂的乘方
积的乘方
计算并说出它们分别是属于哪一种幂的运算.
③ = ( )
问题 一种数码照片的文件大小是27 KB,一个存储量为216 KB的移动存储器能存储多少张这样的数码照片?
分析:这个移动存储器的容量为216 KB,
它能存储这种数码照片的数量为
解:
探究与思考
观察计算结果,你能发现什么规律吗?
= 35-2
= 46-3
用你熟悉的方法填写课本P50表格
猜想:
m-n
am÷an=am-n 其中a≠0,m、n为正整数,且m>n
同底数幂相除,
底数 ,指数 。
不变
相减
同底数幂的除法法则:
请你尝试用文字概括这个结论。
同底数幂
思考:
为什么规定a≠0
a仅仅表示一个字母吗?
理解与应用1
例1:计算
(1) a8÷a3 ; (2)(-a)10÷(-a)3;
( 3)(2a)7÷(2a)4 ; (4)x11÷(-x)5
⑵(-a)10÷(-a)3
解 ⑴ a8÷a3
= a8-3
= a5
= (-a)10-3
= (-a)7
= -a7
⑶(2a)7÷(2a)4
= (2a)7-4
= (2a)3
= 8a3
⑷ x11÷(-x)5
= x11÷(-x 5 )
= - x11÷x5
= - x6
下面的计算对不对?如果不对,怎样改正?
① a10 ÷ a2= a5( ) ② x5 ÷ x4 = x ( )
③a3 ÷a = a3 ( ) ④ (-b)4 ÷ (-b)2 = -b2 ( )
⑤ ( ) ⑥ ( )
a10 ÷ a2= a8
a3 ÷a = a2
(-b)4 ÷ (-b)2 =b2
×
√
×
×
×
×
想一想
比一比,看谁算的快!
题目
答案
巩固练习
例2:计算
(1) a10÷ a5 ÷ a2 (2)(x-1)5÷(1-x)2
解: (1)a10÷a5÷ a2
= a5÷a2
= a3
(2)(x-1)5÷(1-x)2
=(x-1)5÷(x -1)2
=(x-1)3
= -(1-x)5÷(1-x)2
=-(1-x)3
理解与应用2
巩固训练
计算:
(1) a10÷( a5 ÷ a2) (2)(a-b)4÷(b-a)2
(3)(a5) 2 · a3 ÷ (a2)3
1.如果x2m-1 ÷ x2 =xm+1,求m的值.
2. 若10m=16,10n=20,求10m-n的值.
解:∵ x2m-1 ÷ x2 =xm+1 ,
∴ ,
∴ 2m-1-2=m+1,
解得:m=4.
解:∵ 10m =16,10n=20,
∴ 10m-n =10m ÷ 10n =16 ÷ 20=0.8
变式训练
拓展练习
(1)若3x-2y-3=0,则103x÷102y= 。
(2)若xm=6,xn=2,则xm-n = ,
x2m-n = 。
(3)若10m=200,10n=2,则9m÷32 n= 。
1000
3
18
81
归纳小结
1、同底数幂的除法法则:同底数幂相除,底数不变,指数相减。
am÷an = am-n (a≠0,m,n都是正整数,且 m>n)
底数a可以代表一个数、字母、代数式等。
2、计算时的几个注意点:
(1)同底数幂的除法计算,直接应用法则,底数不变,指数相减;
(2)不是同底数幂时,应先化成同底数幂,再计算,注意符号;
(3)当底数是代数式时,应把这个代数式看成一个整体;
(4)混合运算时注意运算的顺序。
