沪科版七年级下册数学 8.2.3单项式与多项式相乘 课件(共21张PPT)
文档属性
| 名称 | 沪科版七年级下册数学 8.2.3单项式与多项式相乘 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 13:56:28 | ||
图片预览







文档简介
(共21张PPT)
1、同底数幂的乘法:
2、幂的乘方:
(m,n均为正整数)
(m,n均为正整数)
3、积的乘方:
(n为正整数)
把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式
单项式与单项式相乘:
判断正误(如果不对应如何改正 )
(1)4a3·2a2=8a6 ( )
(2)
( )
(3)
( )
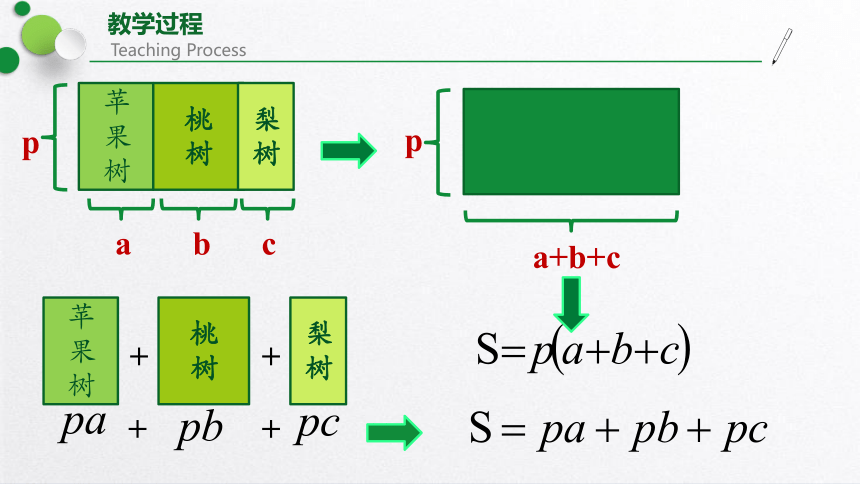
单项式乘以多项式
p a b c
乘法分配律
是否相等
=
乘法分配律:
字母表示:a(b+c)=ac+bc
p
a
b
c
苹
果
树
桃
树
梨
树
这三块地 面积是多少?
a
b
c
p
苹
果
树
桃
树
梨树
p
a+b+c
苹
果
树
桃
树
梨树
+
+
+
+
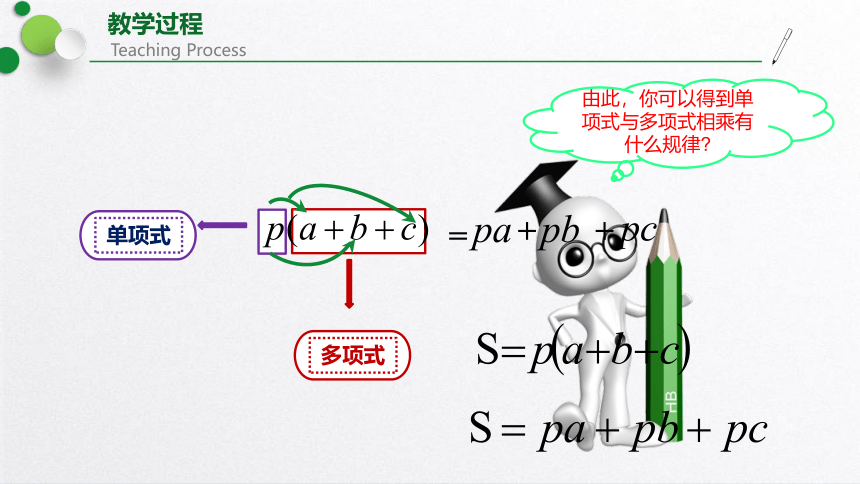
单项式
多项式
=
+
+
由此,你可以得到单项式与多项式相乘有什么规律
根据这个规律:
A
B
由此,你可以得到单项式与多项式相乘有什么规律
+
+
+
注意“符号”
不要“漏乘”
!
不要“漏乘”
注意“符号”
!
不要“漏乘”
+
-
+
注意“符号”
!
由此,你可以得到单项式与多项式相乘有什么规律
例1、火眼金睛:利用法则判断对错
( )
( )
( )
( )
(3) (-4x2) (3x+1);
解:原式 =(-4x2) (3x)+(-4x2) 1
=(-4×3)(x2 x)+(-4x2)
= -12x3 -4x2.
例2. 计算:
解:
1. 计算:
(1)-2x2 · (x-5y);
(2)(3x2-x+1)· 4x .
-2x3+10x2y
12x3-4x2+4x
(3)(2x+1) · (-6x);
(4)3a·(5a-3b) .
-12x2-6x
15a2-9ab
(5)(-3x2)·(4x-3)
(6)2ab(5ab2+3a2b)
(7)(-12xy2-10x2y+21y3)(-6xy3)
10a2b3+6a3b2
72x2y5+60x3y4-126xy6
-12x3+9x2
(8)
a2b3-a2b2
1
4
随堂演练
2、填空
(1)( )
(2)
(3)
(4)已知a2(2ax-3ay)=2a6-3a3,则x= ,y= .
-6ab
2a
1
4ab
8a2b2
4
1
温“心”提示:单项式与多项式相乘,结果有同类项时要合并!
解:原式
当
3、先化简,再求值:
其中
时,原式
客厅
卧室
卫生间
厨房
2a
a
2a
b
2b
小李家住房结构图如图所示,他打算把客厅和卧室铺上地板砖,请你帮他算一下,他至少需要买多少平米地板?
单位:米
解:
答:他至少需要买 平方米地板砖。
不要“漏乘”
注意“符号”
乘法分配律:
单项式×多项式
单项式×单项式
转化
说说你的收获和疑问吧!
单项式与多项式相乘,用单项式去乘多项式的每一项,再把所得的积相加.
单项式与多项式相乘的依据是乘法对加法的分配律.
注意:单项式与多项式相乘,在没有合并同类项前,其积仍是多项式,项数与原多项式的项数相同。积的每一项的符号由原多项式各项符号和单项式的符号来决定。
注意运用去括号法则,不要漏乘项.
通过这节课的学习活动,你有什么收获?
1、同底数幂的乘法:
2、幂的乘方:
(m,n均为正整数)
(m,n均为正整数)
3、积的乘方:
(n为正整数)
把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式
单项式与单项式相乘:
判断正误(如果不对应如何改正 )
(1)4a3·2a2=8a6 ( )
(2)
( )
(3)
( )
单项式乘以多项式
p a b c
乘法分配律
是否相等
=
乘法分配律:
字母表示:a(b+c)=ac+bc
p
a
b
c
苹
果
树
桃
树
梨
树
这三块地 面积是多少?
a
b
c
p
苹
果
树
桃
树
梨树
p
a+b+c
苹
果
树
桃
树
梨树
+
+
+
+
单项式
多项式
=
+
+
由此,你可以得到单项式与多项式相乘有什么规律
根据这个规律:
A
B
由此,你可以得到单项式与多项式相乘有什么规律
+
+
+
注意“符号”
不要“漏乘”
!
不要“漏乘”
注意“符号”
!
不要“漏乘”
+
-
+
注意“符号”
!
由此,你可以得到单项式与多项式相乘有什么规律
例1、火眼金睛:利用法则判断对错
( )
( )
( )
( )
(3) (-4x2) (3x+1);
解:原式 =(-4x2) (3x)+(-4x2) 1
=(-4×3)(x2 x)+(-4x2)
= -12x3 -4x2.
例2. 计算:
解:
1. 计算:
(1)-2x2 · (x-5y);
(2)(3x2-x+1)· 4x .
-2x3+10x2y
12x3-4x2+4x
(3)(2x+1) · (-6x);
(4)3a·(5a-3b) .
-12x2-6x
15a2-9ab
(5)(-3x2)·(4x-3)
(6)2ab(5ab2+3a2b)
(7)(-12xy2-10x2y+21y3)(-6xy3)
10a2b3+6a3b2
72x2y5+60x3y4-126xy6
-12x3+9x2
(8)
a2b3-a2b2
1
4
随堂演练
2、填空
(1)( )
(2)
(3)
(4)已知a2(2ax-3ay)=2a6-3a3,则x= ,y= .
-6ab
2a
1
4ab
8a2b2
4
1
温“心”提示:单项式与多项式相乘,结果有同类项时要合并!
解:原式
当
3、先化简,再求值:
其中
时,原式
客厅
卧室
卫生间
厨房
2a
a
2a
b
2b
小李家住房结构图如图所示,他打算把客厅和卧室铺上地板砖,请你帮他算一下,他至少需要买多少平米地板?
单位:米
解:
答:他至少需要买 平方米地板砖。
不要“漏乘”
注意“符号”
乘法分配律:
单项式×多项式
单项式×单项式
转化
说说你的收获和疑问吧!
单项式与多项式相乘,用单项式去乘多项式的每一项,再把所得的积相加.
单项式与多项式相乘的依据是乘法对加法的分配律.
注意:单项式与多项式相乘,在没有合并同类项前,其积仍是多项式,项数与原多项式的项数相同。积的每一项的符号由原多项式各项符号和单项式的符号来决定。
注意运用去括号法则,不要漏乘项.
通过这节课的学习活动,你有什么收获?
