17.1勾股定理(2) 课件(18张ppt)
文档属性
| 名称 | 17.1勾股定理(2) 课件(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-10 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
17.1勾股定理(2)
人教版八年级下册
教学目标
2. 能应用勾股定理解决简单的实际问题.
1. 能应用勾股定理计算直角三角形的边长.
3. 从实际问题中构造直角三角形解决生产、生活中的有关问题.
复习导入
直角三角形的边、角之间分别存在着什么关系?
这节课我们就来学习用勾股定理解决实际问题.
新知探究
知识点 1
用勾股定理解决问题
例1 一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
已知条件有哪些?
新知探究
观察
1.木板能横着或竖着从门框通过吗?
2.这个门框能通过的最大长度是多少?
不能
3.怎样判定这块木板能否通过木框?
求出斜边的长,与木板的宽比较.
新知探究
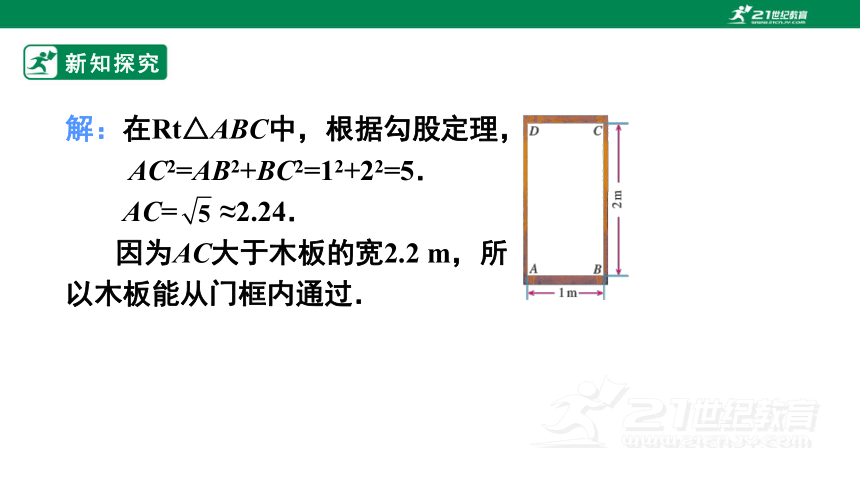
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为AC大于木板的宽2.2 m,所
以木板能从门框内通过.
变式练习
1.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60 m,AC=20m.求A,B两点间的距离(结果取整数).
解:
变式练习
2.如图,在平面直角坐标系中有两点A(5,0)和B(0,4).求这两点之间的距离.
解:由图可知两点之间的距离为AB的长.
例题讲解
例2 如图,一架2.6米长的梯子AB 斜靠在一竖直的墙AO上,这时AO 为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5米,那么梯子底端B也外移0.5米吗?
在Rt△COD中,根据勾股定理,
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15.
解:在Rt△AOB中,根据勾股定理,
OB2=AB2-OA2=2.62-2.42=1. OB=1.
变式练习
3.我国古代数学著作《九章算术》中的一个问题,原文是:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?请用学过的数学知识回答这个问题.
A
B
C
解:设AB=x,则AC=x+1,
有 AB2+BC2=AC2,
可列方程,得 x2+52=(x+1)2 ,
解方程得x=12.
因此x+1=13
答:这个水池的深度是12尺,
这根芦苇的长度是13尺.
变式练习
4、如图《九章算术》中的“折竹抵地”问题:今有今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?
解:如图,设折断处离地面的高度为x尺,
则AB=10-x,BC=6,
在Rt△ABC中,AC2+BC2=AB2,即x2+62=(10-x)2.
解得x=3.2
新知讲解
归纳总结:解决勾股定理的实际问题其关键是根据题意构造直角三角形,结合相应的数据,通过构造方程求解
课堂小结
化非直角三角形为直角三角形
将实际问题转化为直角三角形模型
勾股定理的应用
当堂练习
AC=8
A
B
C
6
10
A
B
C
8
15
A
B
C
2
30°
A
B
C
2
45°
1.求出下列直角三角形中未知的边.
2.如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km, CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
当堂练习
C
A
E
B
D
x
25-x
解:设AE= x km,
根据勾股定理,得
AD2+AE2=DE2,
BC2+BE2=CE2.
又 ∵ DE=CE,
∴ AD2+AE2= BC2+BE2.
即 152+x2=102+(25-x)2
答:E站应建在离A站10km处.
∴ x=10.
则 BE=(25-x)km,
15
10
当堂练习
3.在△ABC中,若AC=15,BC=13,AB边上的高CD=12,则△ABC的周长为( )
A.32 B.42
C.32或42 D.以上都不对
C
解析:如图①,CD在△ABC内部时,AB=AD+BD=9+5=14,此时,△ABC的周长=14+13+15=42,如图②,CD在△ABC 外部时,AB=AD-BD=9-5=4,此时,△ABC的周长=4+13+15=32.综上所述,△ABC的周长为32或42.故选C.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
17.1勾股定理(2)
人教版八年级下册
教学目标
2. 能应用勾股定理解决简单的实际问题.
1. 能应用勾股定理计算直角三角形的边长.
3. 从实际问题中构造直角三角形解决生产、生活中的有关问题.
复习导入
直角三角形的边、角之间分别存在着什么关系?
这节课我们就来学习用勾股定理解决实际问题.
新知探究
知识点 1
用勾股定理解决问题
例1 一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
已知条件有哪些?
新知探究
观察
1.木板能横着或竖着从门框通过吗?
2.这个门框能通过的最大长度是多少?
不能
3.怎样判定这块木板能否通过木框?
求出斜边的长,与木板的宽比较.
新知探究
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为AC大于木板的宽2.2 m,所
以木板能从门框内通过.
变式练习
1.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60 m,AC=20m.求A,B两点间的距离(结果取整数).
解:
变式练习
2.如图,在平面直角坐标系中有两点A(5,0)和B(0,4).求这两点之间的距离.
解:由图可知两点之间的距离为AB的长.
例题讲解
例2 如图,一架2.6米长的梯子AB 斜靠在一竖直的墙AO上,这时AO 为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5米,那么梯子底端B也外移0.5米吗?
在Rt△COD中,根据勾股定理,
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15.
解:在Rt△AOB中,根据勾股定理,
OB2=AB2-OA2=2.62-2.42=1. OB=1.
变式练习
3.我国古代数学著作《九章算术》中的一个问题,原文是:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?请用学过的数学知识回答这个问题.
A
B
C
解:设AB=x,则AC=x+1,
有 AB2+BC2=AC2,
可列方程,得 x2+52=(x+1)2 ,
解方程得x=12.
因此x+1=13
答:这个水池的深度是12尺,
这根芦苇的长度是13尺.
变式练习
4、如图《九章算术》中的“折竹抵地”问题:今有今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?
解:如图,设折断处离地面的高度为x尺,
则AB=10-x,BC=6,
在Rt△ABC中,AC2+BC2=AB2,即x2+62=(10-x)2.
解得x=3.2
新知讲解
归纳总结:解决勾股定理的实际问题其关键是根据题意构造直角三角形,结合相应的数据,通过构造方程求解
课堂小结
化非直角三角形为直角三角形
将实际问题转化为直角三角形模型
勾股定理的应用
当堂练习
AC=8
A
B
C
6
10
A
B
C
8
15
A
B
C
2
30°
A
B
C
2
45°
1.求出下列直角三角形中未知的边.
2.如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km, CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
当堂练习
C
A
E
B
D
x
25-x
解:设AE= x km,
根据勾股定理,得
AD2+AE2=DE2,
BC2+BE2=CE2.
又 ∵ DE=CE,
∴ AD2+AE2= BC2+BE2.
即 152+x2=102+(25-x)2
答:E站应建在离A站10km处.
∴ x=10.
则 BE=(25-x)km,
15
10
当堂练习
3.在△ABC中,若AC=15,BC=13,AB边上的高CD=12,则△ABC的周长为( )
A.32 B.42
C.32或42 D.以上都不对
C
解析:如图①,CD在△ABC内部时,AB=AD+BD=9+5=14,此时,△ABC的周长=14+13+15=42,如图②,CD在△ABC 外部时,AB=AD-BD=9-5=4,此时,△ABC的周长=4+13+15=32.综上所述,△ABC的周长为32或42.故选C.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
