4.2 比较线段的长短 课件(共18张PPT)
文档属性
| 名称 | 4.2 比较线段的长短 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 566.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 19:58:03 | ||
图片预览

文档简介
(共18张PPT)
第四章 几何图形初步
人教版 数学 七年级上册
4.2 直线、射线、线段
A
B
A
B
A
B
A
B
射线和线段都是直线的一部分
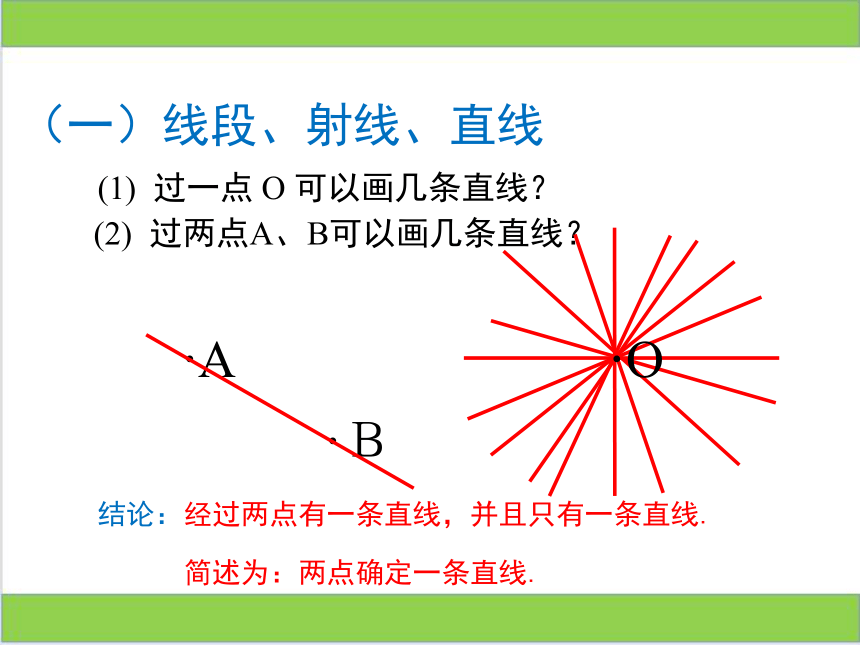
(1) 过一点 O 可以画几条直线?
(2) 过两点A、B可以画几条直线?
·A
·B
·O
结论:经过两点有一条直线,并且只有一条直线.
简述为:两点确定一条直线.
(一)线段、射线、直线
举一个能反映“经过两点有且只有一条直线”的实例.
植树时,只要定出两个树坑的位置就能确定同一行的树坑所在的直线.
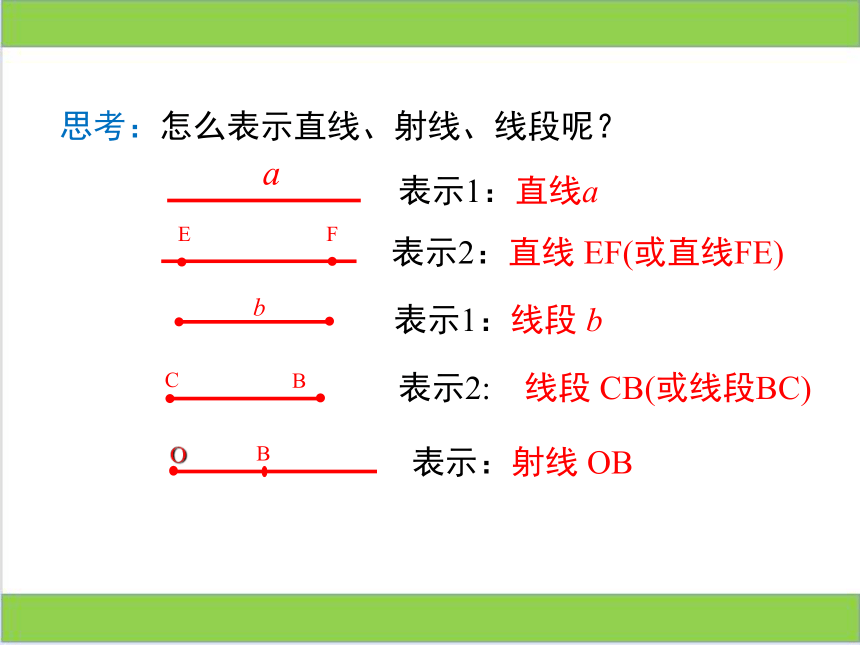
思考:怎么表示直线、射线、线段呢?
C
B
表示2: 线段 CB(或线段BC)
b
表示1:线段 b
B
O
表示:射线 OB
E
F
表示2:直线 EF(或直线FE)
a
表示1:直线a
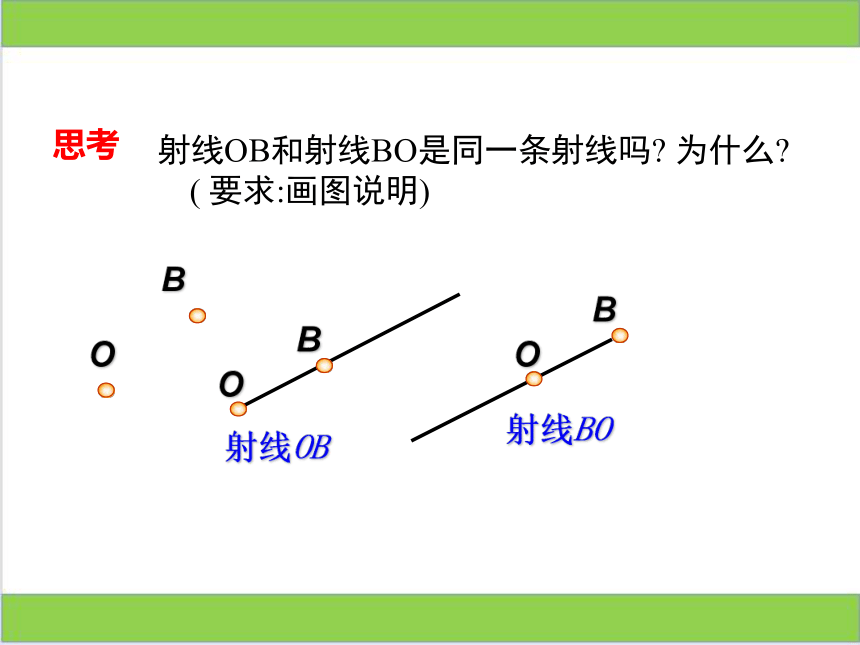
射线OB和射线BO是同一条射线吗 为什么
( 要求:画图说明)
O
B
O
B
射线OB
O
B
射线BO
思考
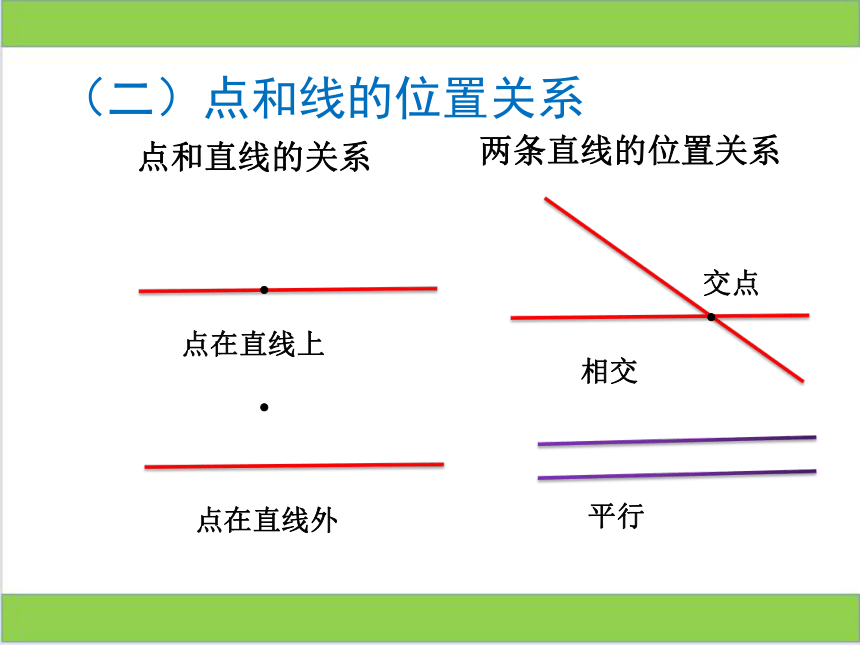
点和直线的关系
两条直线的位置关系
(二)点和线的位置关系
点在直线上
点在直线外
相交
平行
交点
思考:怎样比较两条线段的长短 ?
(1) 度量法
(2) 叠合法
将其中一条线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上.
用刻度尺量出它们的长度,再进行比较.
A B
C D
a
b
(三)线段的长短
例1 如图,已知线段AB,用尺规作一条线段等于已知线段AB.
(1)作射线A'C';
(2)用圆规在射线A'C'上截取A'B'=AB.
(3)线段A'B'为所求作的线段.
A' C'
B'
A
B
解:作图步骤如下:
及时练习:如图,已知线段a,b,用尺规作线段AB=a+b ,CD=a-b
解:如图所示:
(1)作射线AM;
(2)用圆规在射线AM上截取AC=a,CB=b;
(3)线段AB为所求作的线段.
a
b
如图所示:
(1)作射线AM;
(2)用圆规在射线AM上截取AC=a,CD=b;
(3)线段AD为所求作的线段.
A
C
B
M
M
C
D
A
A
B
如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你在图上画出最短路线.
发现:两点之间的所有连线中,线段最短。
简述为:两点之间,线段最短
我们把两点之间线段的长度,叫做这两点之间的距离.
例2 如图所示,直线MN表示一条铁路,铁路两旁各有一点A和B,表示两个工厂.要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?
解:连接AB,交MN于点P,则这个货站应建在点P处.
P
P
如何找到一条绳子的中点呢?
(四)线段的中点
谁可以描述一下线段中点的概念呢?(对照图形)
点M把线段AB分成相等的两条线段AM和BM,点M叫做线段AB的中点.
因为M是线段AB的中点
所以AM= MB = AB
(或AB=2AM=2MB)
1
2
中点定义
数学语言:
及时练习:如图,AB=6 cm,点C是线段AB的中点,则AC的长度是 .
3 cm
例3 如图,在直线上有A,B,C三点,AB=4 cm,BC=3 cm,如果O是线段AC的中点,求线段OB的长度.
解:因为AB=4 cm,BC=3 cm,
所以AC=AB+ BC=7 cm.
因为点O是线段AC的中点,
所以OC= AC=3.5 cm.
所以OB=OC-BC=3.5-3=0.5(cm).
变式练习:如果线段AB=6,点C在直线AB上,BC=4,D是AC的中点,那么A、D两点间的距离是( )
A.5 B.2.5 C.5或2.5 D.5或1
(1)当点C在线段AB上时,如图:
(2)当点C在线段AB的延长线上时,如图:
D
分类讨论
数形结合
直线、射线、线段
比较线段的长短
两点之间线段最短
线段的中点
表示方法
两点确定一条直线
度量法
叠合法
尺规作图
数学语言
应用
应用
课堂小结:
分类讨论数形结合
第四章 几何图形初步
人教版 数学 七年级上册
4.2 直线、射线、线段
A
B
A
B
A
B
A
B
射线和线段都是直线的一部分
(1) 过一点 O 可以画几条直线?
(2) 过两点A、B可以画几条直线?
·A
·B
·O
结论:经过两点有一条直线,并且只有一条直线.
简述为:两点确定一条直线.
(一)线段、射线、直线
举一个能反映“经过两点有且只有一条直线”的实例.
植树时,只要定出两个树坑的位置就能确定同一行的树坑所在的直线.
思考:怎么表示直线、射线、线段呢?
C
B
表示2: 线段 CB(或线段BC)
b
表示1:线段 b
B
O
表示:射线 OB
E
F
表示2:直线 EF(或直线FE)
a
表示1:直线a
射线OB和射线BO是同一条射线吗 为什么
( 要求:画图说明)
O
B
O
B
射线OB
O
B
射线BO
思考
点和直线的关系
两条直线的位置关系
(二)点和线的位置关系
点在直线上
点在直线外
相交
平行
交点
思考:怎样比较两条线段的长短 ?
(1) 度量法
(2) 叠合法
将其中一条线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上.
用刻度尺量出它们的长度,再进行比较.
A B
C D
a
b
(三)线段的长短
例1 如图,已知线段AB,用尺规作一条线段等于已知线段AB.
(1)作射线A'C';
(2)用圆规在射线A'C'上截取A'B'=AB.
(3)线段A'B'为所求作的线段.
A' C'
B'
A
B
解:作图步骤如下:
及时练习:如图,已知线段a,b,用尺规作线段AB=a+b ,CD=a-b
解:如图所示:
(1)作射线AM;
(2)用圆规在射线AM上截取AC=a,CB=b;
(3)线段AB为所求作的线段.
a
b
如图所示:
(1)作射线AM;
(2)用圆规在射线AM上截取AC=a,CD=b;
(3)线段AD为所求作的线段.
A
C
B
M
M
C
D
A
A
B
如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你在图上画出最短路线.
发现:两点之间的所有连线中,线段最短。
简述为:两点之间,线段最短
我们把两点之间线段的长度,叫做这两点之间的距离.
例2 如图所示,直线MN表示一条铁路,铁路两旁各有一点A和B,表示两个工厂.要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?
解:连接AB,交MN于点P,则这个货站应建在点P处.
P
P
如何找到一条绳子的中点呢?
(四)线段的中点
谁可以描述一下线段中点的概念呢?(对照图形)
点M把线段AB分成相等的两条线段AM和BM,点M叫做线段AB的中点.
因为M是线段AB的中点
所以AM= MB = AB
(或AB=2AM=2MB)
1
2
中点定义
数学语言:
及时练习:如图,AB=6 cm,点C是线段AB的中点,则AC的长度是 .
3 cm
例3 如图,在直线上有A,B,C三点,AB=4 cm,BC=3 cm,如果O是线段AC的中点,求线段OB的长度.
解:因为AB=4 cm,BC=3 cm,
所以AC=AB+ BC=7 cm.
因为点O是线段AC的中点,
所以OC= AC=3.5 cm.
所以OB=OC-BC=3.5-3=0.5(cm).
变式练习:如果线段AB=6,点C在直线AB上,BC=4,D是AC的中点,那么A、D两点间的距离是( )
A.5 B.2.5 C.5或2.5 D.5或1
(1)当点C在线段AB上时,如图:
(2)当点C在线段AB的延长线上时,如图:
D
分类讨论
数形结合
直线、射线、线段
比较线段的长短
两点之间线段最短
线段的中点
表示方法
两点确定一条直线
度量法
叠合法
尺规作图
数学语言
应用
应用
课堂小结:
分类讨论数形结合
