5.5.1两角差的 余弦公式 课件(共15张PPT)
文档属性
| 名称 | 5.5.1两角差的 余弦公式 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 363.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
5.5.1两角差的
余弦公式
授课老师:某某某
学习目标及重难点
难点
1、两角差的余弦公式的推导过程
2、两角差的余弦公式的灵活运用
重点
两角差的余弦公式的应用
学习目标
1.通过探究,了解两角差的余弦公式的推导过程
2.熟记两角差的余弦公式的形式及符号特征,并能利用该公式进行求值、计算
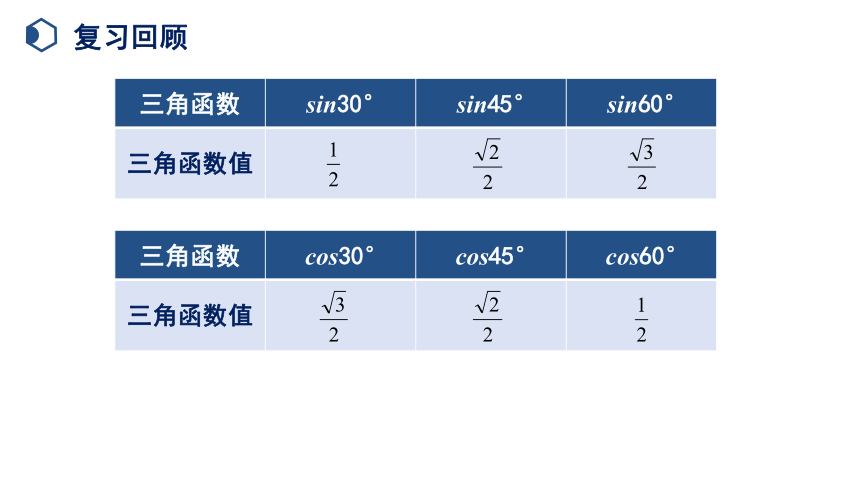
复习回顾
三角函数 sin30° sin45° sin60°
三角函数值
三角函数 cos30° cos45° cos60°
三角函数值
新课引入
问题1:如何计算cos15 ?
cos(60 -45 )
=
cos(45 -30 )
=
cos15 =
cos15 =
问题2:设α,β为两个任意角,那么
cos(α-β) = cosα-cosβ 恒成立吗?
问题3:如何计算cos(α-β)
新课内容
设单位圆与x轴的正半轴相交于点A(1,0),以x轴非负半轴为始边,作角α,β,α-β,且α,β终边不重合
o
x
y
角α终边
P1
A1
角β终边
P
角α-β终边
A
P1(cosα,sinα) A1(cosβ,sinβ)
P(cos(α-β),sin(α-β))
α-β
α-β
∠POA=∠P1OA1=α-β
连接PA,P1A1,则△AOP≌△A1OP1
那么 A1P1=AP
根据两点间距离公式得,
新课内容
化简得
cos(α-β) = cosα cosβ + sinα sinβ
当角α,β终边相同时,上式是否成立?
∵角α,β终边相同 ∴α=β+2kπ,k∈Z
∴左式=cos(α-β)=cos2kπ=cos0=1
∴右式=cos(β+2kπ) cosβ + sin(β+2kπ)sinβ=cos2β+sin2β =1
∴左式=右式
∴当角α,β终边相同时,也满足公式
代入验证:
两角差的余弦公式
对于任意角α,β有
上述公式称为差角的余弦公式,简记作
(3)同名积,符号反,CCSS.
注意:
(1)公式中的α,β是任意角;
(2)公式的结构特点:左边是“两角差的余弦值”,
右边是“这两角余弦积与正弦积的和”;
题型1 两角差的余弦公式的正用和逆用
例1:利用差角余弦公式求cos15
解法1:
解法2:
cos15 = cos(45 -30 )
= cos60 cos45 +sin60 sin45
= cos45 cos30 +sin45 sin30
cos15 = cos(60 -45 )
=
=
=
=
知识点: 1.把非特殊角拆分成特殊角的差.
2.公式的直接应用.
题型1 两角差的余弦公式的正用和逆用
例2:cos175 cos55 +sin175 sin55
知识点:1.根据CCSS识别两角差的余弦公式
2.公式的逆运算应用.
解:原式=cos(175 -55 )
=cos(120 )
题型1 两角差的余弦公式的正用和逆用
例3:利用公式 C(α-β)证明:
证明:
发现上述诱导公式与差角的余弦公式间的联系.
题型2 给值求值
例4:
解:
题型2 给值求值
变4:
解:
(1)从角的关系中找解题思路:已知某些角的三角函数值,求另外一些角的三角函数值,要注意观察已知角与所求表达式中角的关系,根据需要灵活地进行拆角或凑角的变换.
规律方法:给值求值问题的解题策略
课堂练习
解:(1)原式=cos(15 -105 )=cos(-90 )=cos 90 =0.
(2)原式=sin 30 sin 60 +cos 30 cos 60
课堂小结
01两角差的余弦公式
两角差的余弦公式
02两角差的余弦公式应用
cos(α-β) = cosα cosβ + sinα sinβ
两角差的余弦公式的逆用及其应用
给值求值
5.5.1两角差的
余弦公式
授课老师:某某某
学习目标及重难点
难点
1、两角差的余弦公式的推导过程
2、两角差的余弦公式的灵活运用
重点
两角差的余弦公式的应用
学习目标
1.通过探究,了解两角差的余弦公式的推导过程
2.熟记两角差的余弦公式的形式及符号特征,并能利用该公式进行求值、计算
复习回顾
三角函数 sin30° sin45° sin60°
三角函数值
三角函数 cos30° cos45° cos60°
三角函数值
新课引入
问题1:如何计算cos15 ?
cos(60 -45 )
=
cos(45 -30 )
=
cos15 =
cos15 =
问题2:设α,β为两个任意角,那么
cos(α-β) = cosα-cosβ 恒成立吗?
问题3:如何计算cos(α-β)
新课内容
设单位圆与x轴的正半轴相交于点A(1,0),以x轴非负半轴为始边,作角α,β,α-β,且α,β终边不重合
o
x
y
角α终边
P1
A1
角β终边
P
角α-β终边
A
P1(cosα,sinα) A1(cosβ,sinβ)
P(cos(α-β),sin(α-β))
α-β
α-β
∠POA=∠P1OA1=α-β
连接PA,P1A1,则△AOP≌△A1OP1
那么 A1P1=AP
根据两点间距离公式得,
新课内容
化简得
cos(α-β) = cosα cosβ + sinα sinβ
当角α,β终边相同时,上式是否成立?
∵角α,β终边相同 ∴α=β+2kπ,k∈Z
∴左式=cos(α-β)=cos2kπ=cos0=1
∴右式=cos(β+2kπ) cosβ + sin(β+2kπ)sinβ=cos2β+sin2β =1
∴左式=右式
∴当角α,β终边相同时,也满足公式
代入验证:
两角差的余弦公式
对于任意角α,β有
上述公式称为差角的余弦公式,简记作
(3)同名积,符号反,CCSS.
注意:
(1)公式中的α,β是任意角;
(2)公式的结构特点:左边是“两角差的余弦值”,
右边是“这两角余弦积与正弦积的和”;
题型1 两角差的余弦公式的正用和逆用
例1:利用差角余弦公式求cos15
解法1:
解法2:
cos15 = cos(45 -30 )
= cos60 cos45 +sin60 sin45
= cos45 cos30 +sin45 sin30
cos15 = cos(60 -45 )
=
=
=
=
知识点: 1.把非特殊角拆分成特殊角的差.
2.公式的直接应用.
题型1 两角差的余弦公式的正用和逆用
例2:cos175 cos55 +sin175 sin55
知识点:1.根据CCSS识别两角差的余弦公式
2.公式的逆运算应用.
解:原式=cos(175 -55 )
=cos(120 )
题型1 两角差的余弦公式的正用和逆用
例3:利用公式 C(α-β)证明:
证明:
发现上述诱导公式与差角的余弦公式间的联系.
题型2 给值求值
例4:
解:
题型2 给值求值
变4:
解:
(1)从角的关系中找解题思路:已知某些角的三角函数值,求另外一些角的三角函数值,要注意观察已知角与所求表达式中角的关系,根据需要灵活地进行拆角或凑角的变换.
规律方法:给值求值问题的解题策略
课堂练习
解:(1)原式=cos(15 -105 )=cos(-90 )=cos 90 =0.
(2)原式=sin 30 sin 60 +cos 30 cos 60
课堂小结
01两角差的余弦公式
两角差的余弦公式
02两角差的余弦公式应用
cos(α-β) = cosα cosβ + sinα sinβ
两角差的余弦公式的逆用及其应用
给值求值
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
