5.4.2正弦函数、余弦函数的性质 课件(共20张PPT)
文档属性
| 名称 | 5.4.2正弦函数、余弦函数的性质 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 932.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 17:40:16 | ||
图片预览







文档简介
(共20张PPT)
5.4三角函数的图象与性质
5.4.2正弦函数、余弦函数的性质
授课老师:某某某
学习目标及重难点
学习目标
2.理解正弦函数与余弦函数的周期性,会求函数的周期,提升数学抽象、数学运算素养
1.了解周期函数的概念
3.理解三角函数的奇偶性以及对称性,会判断给定函数的奇偶性
复习回顾
正弦函数、余弦函数的简图怎么画吗?
五点作图法
y=sin x
y=cos x
正弦函数y=sinx
余弦函数y=cosx
新课引入
问题1:类比以往对函数性质的研究,你认为应研究正弦函数、余弦函数的哪些性质?
单调性
最值
定义域
值域
奇偶性
新课内容
探究1:周期性
今天星期几? 7天后星期几?
14天后呢? 100天后呢?……
世界上有许多事物都呈现“周而复始”的变化规律,如年有四季更替,月有阴晴圆缺,这种现象在数学上称为周期性,在函数领域里,周期性是函数的一个重要性质。
新课内容
问题2:观察正弦函数图像,有什么特点?
正弦函数值具有的“周而复始”的变化规律
(1)正弦函数的图象是有规律不断重复出现的;
(2)规律是:每隔2π重复出现一次(或者说每隔2kπ,k∈Z重复出现);
诱导公式一:sin(2kπ+x)=sinx(k∈Z)
若f(x)=sinx,则 f(x+2kπ)=f(x)
正、余弦函数的周期性
最小正周期的定义: 如果在周期函数f(x)的所有周期中存在一个最小的正数,
则这个最小正数叫做f(x)的最小正周期.
附:今后本书中所涉及的周期,如果不加特别说明,都是指最小正周期.
一般地,设函数f(x)的定义域为D,如果存在一个非零常数T,使得对每一个x D都有x+T D,且
那么函数f(x)就叫做周期函数,非零常数T就叫做这个函数的周期.
f(x+T)=f(x)
新课内容
说明
2.周期函数的周期不唯一.若T是函数f(x)的最小正周期,则kT(k∈Z,k≠0)也是函数f(x)的周期.
3.并不是所有的周期函数都有最小正周期.
例如,对于函数f(x)=C,(C为常数) 所有非零实数T都是它的周期,而最小正周期是不存在的,所以常数函数没有最小正周期.
1.对周期函数与周期定义中的“当x取定义域内的每一个值时”,要特别注意其中“每一个”的要求.如果只是对某些x有f(x+T)=f(x),那么T就不是f(x)的周期.
新课内容
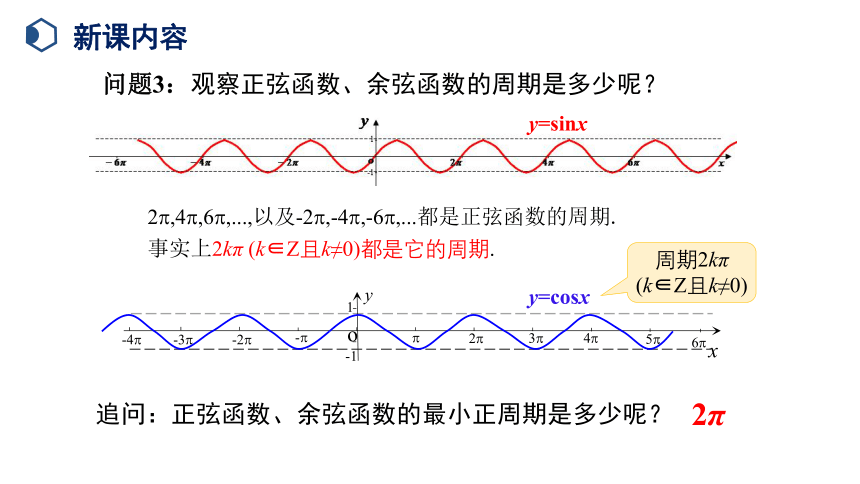
问题3:观察正弦函数、余弦函数的周期是多少呢?
追问:正弦函数、余弦函数的最小正周期是多少呢?
y=sinx
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cosx
2 ,4 ,6 ,...,以及-2 ,-4 ,-6 ,...都是正弦函数的周期.事实上2kπ (k∈Z且k≠0)都是它的周期.
周期2kπ (k∈Z且k≠0)
2π
概念辨析
任意性
周期函数的定义域一定为无限集
等式 f(x+T)=f(x). 强调x本身加的常数才是周期
例题探究
例1:求下列函数的周期
解:(1)∵cos(x+2π)=cosx,
∴3cos(x+2π)=3cosx,
∴函数y= 3cosx,x∈R的周期为2π
由周期函数的定义可知,函数y= sin 2x的周期为π.
即sin (z+2π)= sin z,
于是sin(2x+2π)= sin 2x,所以sin 2(x+π)= sin 2x,x∈R.
(2)令z=2x,由x∈R得z∈R,且y=sin z的周期为2π,
例题探究
例1:求下列函数的周期
解:
新课内容
问题4:回顾上题解答过程,你能发现这些函数的周期与解析中哪些量有关吗?
函数 周期
y=3cos x
y=sin 2x
与x的系数有关
仿照上述分析过程可得函数y=Asin(ωx+φ)、y=Acos(ωx+φ) (其中A,ω,φ为常数,且A≠0,ω>0)的最小正周期为:T= .
A≠0,ω ≠0,最小正周期为:T= .
练习巩固
(5) y=|sin x|,x∈R
(
(
求函数最小正周期的常用方法:
(1)定义法: 利用周期函数的定义求解.
(2)公式法: T= .
(3)图象法: 通过图象直接观察即可.
练习巩固
3.若函数满足,且。则的值为多少?
2. 函数y=最小正周期是4,求的值。
新课内容
探究2:奇偶性
问题5:观察正弦曲线和余弦曲线的对称性,你有什么发现?
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
正弦曲线关于原点对称
正弦函数y=sinx是奇函数
新课内容
探究2:奇偶性
问题5:观察正弦曲线和余弦曲线的对称性,你有什么发现?
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦曲线关于y轴对称
余弦函数y=cosx是偶函数
新课内容
思考:知道一个函数具有周期性和奇偶性,对研究它的图像及其他性质有什么帮助?
可以先考察这个函数在y轴左右半个周期上的图象与性质,然后在根据奇偶性、周期性进行拓展,例如sinx
关于原点对称
向左、右平 移个单位
正弦函数图像
练习巩固
4. 判断下列函数的奇偶性
解:(1)已知x∈R ,所以定义域关于原点对称
f(-x)=-sin(-3x)=sin3x=-f(x),为奇函数
(2)已知x∈R ,所以定义域关于原点对称
f(-x)=sin(-x)+1=-sinx+1,非奇非偶
(3)已知x∈R ,所以定义域关于原点对称
f(-x)=|cos(-x)|=|cosx|,偶函数
课堂小结
函数 y=sin x(x∈R) y=cos x (x∈R)
图像
周期
奇偶性 奇函数 偶函数
T=2π
T=2π
5.4三角函数的图象与性质
5.4.2正弦函数、余弦函数的性质
授课老师:某某某
学习目标及重难点
学习目标
2.理解正弦函数与余弦函数的周期性,会求函数的周期,提升数学抽象、数学运算素养
1.了解周期函数的概念
3.理解三角函数的奇偶性以及对称性,会判断给定函数的奇偶性
复习回顾
正弦函数、余弦函数的简图怎么画吗?
五点作图法
y=sin x
y=cos x
正弦函数y=sinx
余弦函数y=cosx
新课引入
问题1:类比以往对函数性质的研究,你认为应研究正弦函数、余弦函数的哪些性质?
单调性
最值
定义域
值域
奇偶性
新课内容
探究1:周期性
今天星期几? 7天后星期几?
14天后呢? 100天后呢?……
世界上有许多事物都呈现“周而复始”的变化规律,如年有四季更替,月有阴晴圆缺,这种现象在数学上称为周期性,在函数领域里,周期性是函数的一个重要性质。
新课内容
问题2:观察正弦函数图像,有什么特点?
正弦函数值具有的“周而复始”的变化规律
(1)正弦函数的图象是有规律不断重复出现的;
(2)规律是:每隔2π重复出现一次(或者说每隔2kπ,k∈Z重复出现);
诱导公式一:sin(2kπ+x)=sinx(k∈Z)
若f(x)=sinx,则 f(x+2kπ)=f(x)
正、余弦函数的周期性
最小正周期的定义: 如果在周期函数f(x)的所有周期中存在一个最小的正数,
则这个最小正数叫做f(x)的最小正周期.
附:今后本书中所涉及的周期,如果不加特别说明,都是指最小正周期.
一般地,设函数f(x)的定义域为D,如果存在一个非零常数T,使得对每一个x D都有x+T D,且
那么函数f(x)就叫做周期函数,非零常数T就叫做这个函数的周期.
f(x+T)=f(x)
新课内容
说明
2.周期函数的周期不唯一.若T是函数f(x)的最小正周期,则kT(k∈Z,k≠0)也是函数f(x)的周期.
3.并不是所有的周期函数都有最小正周期.
例如,对于函数f(x)=C,(C为常数) 所有非零实数T都是它的周期,而最小正周期是不存在的,所以常数函数没有最小正周期.
1.对周期函数与周期定义中的“当x取定义域内的每一个值时”,要特别注意其中“每一个”的要求.如果只是对某些x有f(x+T)=f(x),那么T就不是f(x)的周期.
新课内容
问题3:观察正弦函数、余弦函数的周期是多少呢?
追问:正弦函数、余弦函数的最小正周期是多少呢?
y=sinx
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cosx
2 ,4 ,6 ,...,以及-2 ,-4 ,-6 ,...都是正弦函数的周期.事实上2kπ (k∈Z且k≠0)都是它的周期.
周期2kπ (k∈Z且k≠0)
2π
概念辨析
任意性
周期函数的定义域一定为无限集
等式 f(x+T)=f(x). 强调x本身加的常数才是周期
例题探究
例1:求下列函数的周期
解:(1)∵cos(x+2π)=cosx,
∴3cos(x+2π)=3cosx,
∴函数y= 3cosx,x∈R的周期为2π
由周期函数的定义可知,函数y= sin 2x的周期为π.
即sin (z+2π)= sin z,
于是sin(2x+2π)= sin 2x,所以sin 2(x+π)= sin 2x,x∈R.
(2)令z=2x,由x∈R得z∈R,且y=sin z的周期为2π,
例题探究
例1:求下列函数的周期
解:
新课内容
问题4:回顾上题解答过程,你能发现这些函数的周期与解析中哪些量有关吗?
函数 周期
y=3cos x
y=sin 2x
与x的系数有关
仿照上述分析过程可得函数y=Asin(ωx+φ)、y=Acos(ωx+φ) (其中A,ω,φ为常数,且A≠0,ω>0)的最小正周期为:T= .
A≠0,ω ≠0,最小正周期为:T= .
练习巩固
(5) y=|sin x|,x∈R
(
(
求函数最小正周期的常用方法:
(1)定义法: 利用周期函数的定义求解.
(2)公式法: T= .
(3)图象法: 通过图象直接观察即可.
练习巩固
3.若函数满足,且。则的值为多少?
2. 函数y=最小正周期是4,求的值。
新课内容
探究2:奇偶性
问题5:观察正弦曲线和余弦曲线的对称性,你有什么发现?
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
正弦曲线关于原点对称
正弦函数y=sinx是奇函数
新课内容
探究2:奇偶性
问题5:观察正弦曲线和余弦曲线的对称性,你有什么发现?
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦曲线关于y轴对称
余弦函数y=cosx是偶函数
新课内容
思考:知道一个函数具有周期性和奇偶性,对研究它的图像及其他性质有什么帮助?
可以先考察这个函数在y轴左右半个周期上的图象与性质,然后在根据奇偶性、周期性进行拓展,例如sinx
关于原点对称
向左、右平 移个单位
正弦函数图像
练习巩固
4. 判断下列函数的奇偶性
解:(1)已知x∈R ,所以定义域关于原点对称
f(-x)=-sin(-3x)=sin3x=-f(x),为奇函数
(2)已知x∈R ,所以定义域关于原点对称
f(-x)=sin(-x)+1=-sinx+1,非奇非偶
(3)已知x∈R ,所以定义域关于原点对称
f(-x)=|cos(-x)|=|cosx|,偶函数
课堂小结
函数 y=sin x(x∈R) y=cos x (x∈R)
图像
周期
奇偶性 奇函数 偶函数
T=2π
T=2π
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
