5.2 运动的合成与分解 高一物理下学期同步学案 典例 练习(人教版2019必修第二册)(含答案)
文档属性
| 名称 | 5.2 运动的合成与分解 高一物理下学期同步学案 典例 练习(人教版2019必修第二册)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-09 22:02:36 | ||
图片预览


文档简介
5.2 运动的合成与分解
一、一个平面运动的实例——观察蜡块的运动
1.建立坐标系
研究蜡块在平面内的运动,可以选择建立 .
如图所示,以蜡块开始匀速运动的位置为原点O,以水平向右的方向和竖直向上的方向分别为x轴和y轴的方向,建立平面直角坐标系.
2.蜡块运动的位置:玻璃管向右匀速平移的速度设为vx,蜡块沿玻璃管匀速上升的速度设为vy,在某时刻t,蜡块的位置P的坐标:x= ,y= .
3.蜡块运动的轨迹:将x、y消去t,得到y= ,可见蜡块的运动轨迹是一条过原点的直线.
4.蜡块运动的速度:大小v= ,方向满足tan θ= .
二、运动的合成与分解
1.合运动与分运动
如果物体同时参与了几个运动,那么物体实际发生的运动就是 ,同时参与的几个运动就是 .
2.运动的合成与分解:已知分运动求合运动的过程,叫作运动的 ;已知合运动求分运动的过程,叫作运动的 .
3.运动的合成与分解遵循 运算法则.
考点一:研究蜡块运动的分解
【例1】红蜡块R可在竖直放置、两端封闭、充满清水的玻璃管中匀速上升。在红蜡块沿玻璃管匀速上升的同时,将玻璃管沿水平方向运动,以蜡块开始运动的位置为原点O,以水平向右的方向和竖直向上的方向分别为x轴和y轴的方向,如图所示,关于红蜡块的运动说法正确的是( )
A.若玻璃管沿x轴正方向做匀速直线运动,红蜡块的运动轨迹一定是直线
B.无论玻璃管沿x轴正方向做何种运动,红蜡块的运动轨迹一定是直线
C.若玻璃管沿x轴正方向做匀加速直线运动,红蜡块速度的大小可能不变
D.若玻璃管沿x轴正方向做匀加速直线运动,红蜡块上升到顶端的时间会变长
【变式练习】
1.在研究运动的合成与分解时,某同学用红蜡块的运动来进行实验,如图所示,红蜡块在长约为1m的玻璃管中从底部沿竖直方向向上做匀速直线运动,同时该同学拿着玻璃管由静止沿水平方向向右做匀加速直线运动,则该过程中关于红蜡块运动情况的描述正确的是( )
A. B.
C. D.
2.竖直放置的封闭玻璃管内注满清水,内部有一个红蜡块。玻璃管倒置时蜡块以3m/s的速度向上匀速运动。在蜡块上升的同时,玻璃管以4m/s的速度水平向右运动,如图所示,此时蜡块实际运动的速度大小是( )
A.5m/s B.6m/s C.7m/s D.8m/s
考点二:互成角度的两个匀速直线运动的合成
【例2】骑射项目是运动会上常见的一种娱乐项目,运动员骑在奔驰的马背上,弯弓射箭射击侧向的靶子目标M,其运动模型简化为如图所示的情境,假设运动员沿方向骑马的速度为,运动员静止时射出的弓箭速度为,直线跑道离固定目标M的最近距离为,假设运动员射箭位置与靶子等高,且垂直跑道方向射出弓箭。不计空气阻力和弓箭的重力,则运动员射出弓箭点的位置距离O点的距离x为( )
A. B. C. D.
【变式练习】
1.小船过河时,垂直河岸方向的分速度为4m/s,沿河岸方向的分速度为3m/s,如图所示,小船过河的实际速度大小为( )
A.3m/s B.4m/s C.5m/s D.7m/s
2.春节期间人们放飞孔明灯表达对新年的祝福,如图所示,若孔明灯在竖直方向做匀速运动,在水平方向做匀速运动,孔明灯的运动轨迹可能为( )
A.直线 B.直线 C.曲线 D.曲线
考点三:一个匀速和一个变速运动的合成
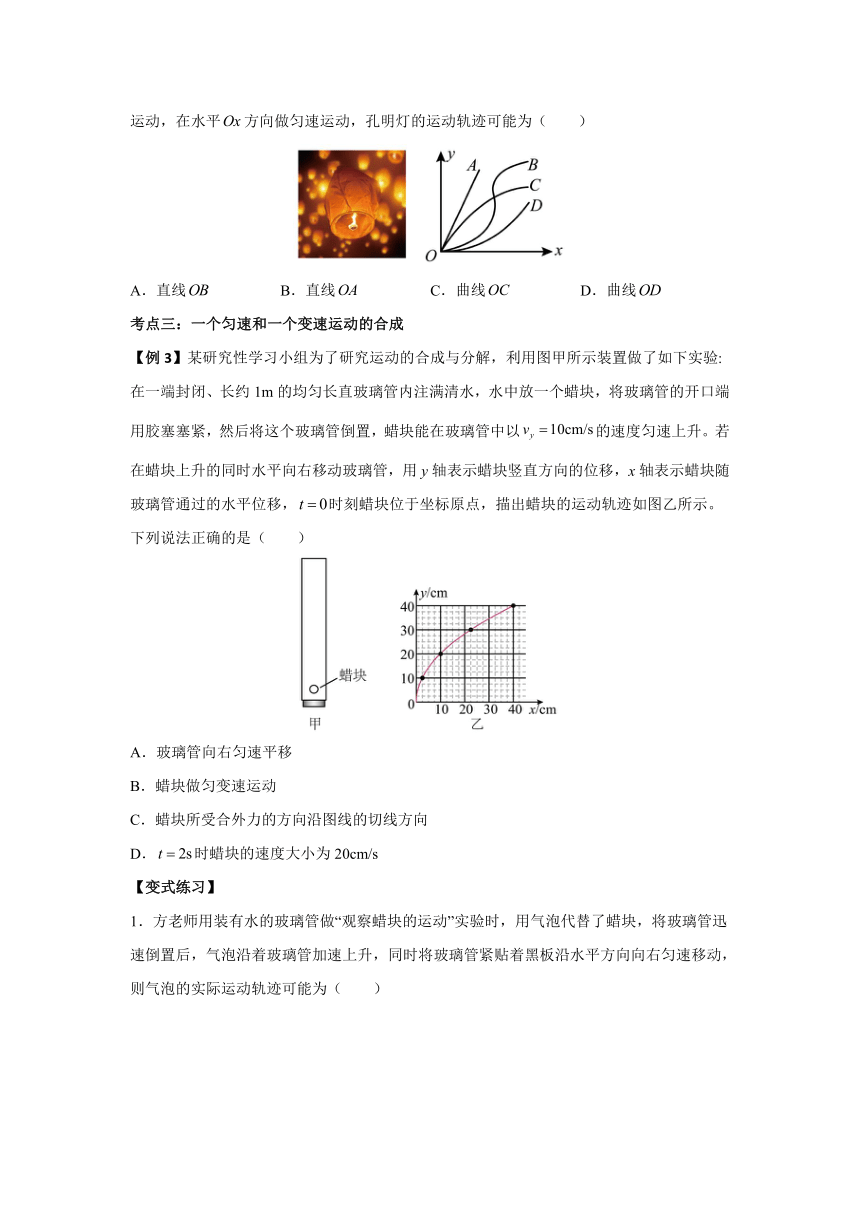
【例3】某研究性学习小组为了研究运动的合成与分解,利用图甲所示装置做了如下实验:在一端封闭、长约1m的均匀长直玻璃管内注满清水,水中放一个蜡块,将玻璃管的开口端用胶塞塞紧,然后将这个玻璃管倒置,蜡块能在玻璃管中以的速度匀速上升。若在蜡块上升的同时水平向右移动玻璃管,用y轴表示蜡块竖直方向的位移,x轴表示蜡块随玻璃管通过的水平位移,时刻蜡块位于坐标原点,描出蜡块的运动轨迹如图乙所示。下列说法正确的是( )
A.玻璃管向右匀速平移
B.蜡块做匀变速运动
C.蜡块所受合外力的方向沿图线的切线方向
D.时蜡块的速度大小为20cm/s
【变式练习】
1.方老师用装有水的玻璃管做“观察蜡块的运动”实验时,用气泡代替了蜡块,将玻璃管迅速倒置后,气泡沿着玻璃管加速上升,同时将玻璃管紧贴着黑板沿水平方向向右匀速移动,则气泡的实际运动轨迹可能为( )
A. B.
C. D.
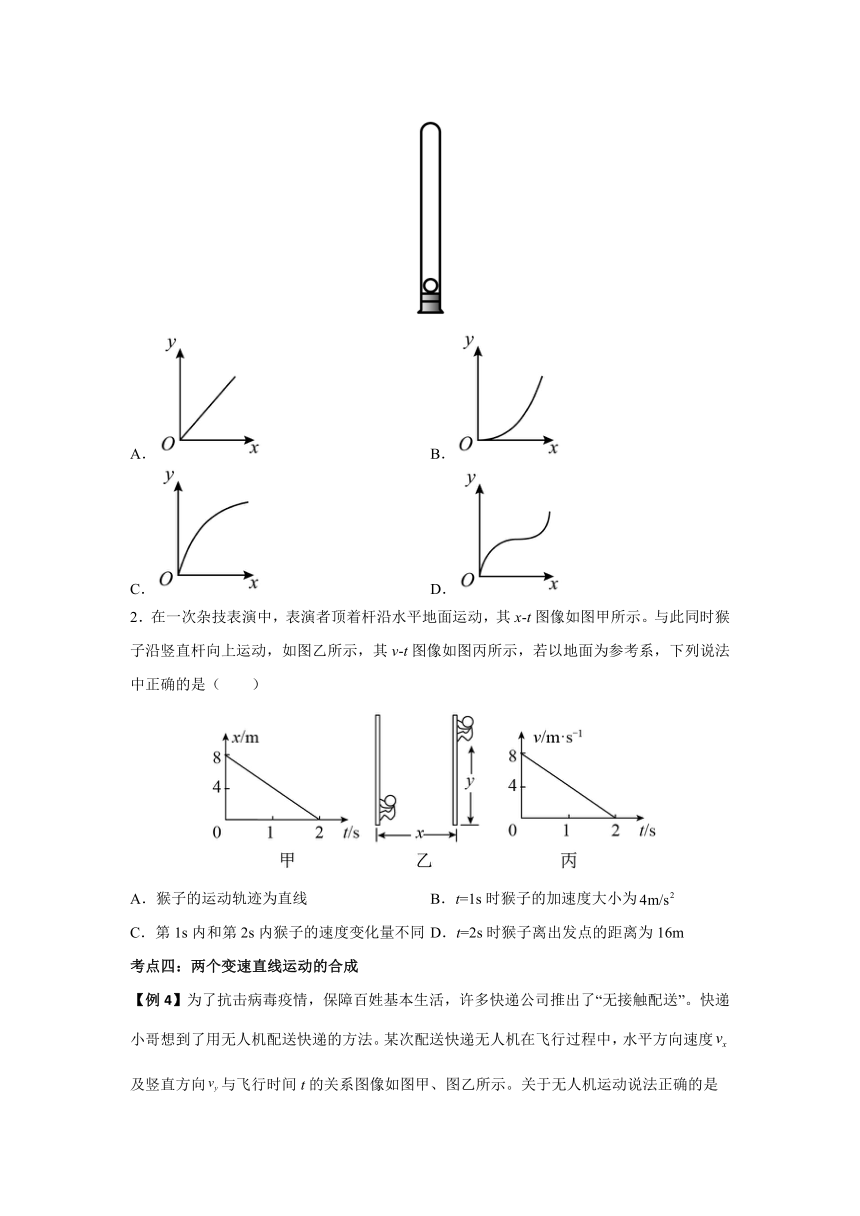
2.在一次杂技表演中,表演者顶着杆沿水平地面运动,其x-t图像如图甲所示。与此同时猴子沿竖直杆向上运动,如图乙所示,其v-t图像如图丙所示,若以地面为参考系,下列说法中正确的是( )
A.猴子的运动轨迹为直线 B.t=1s时猴子的加速度大小为
C.第1s内和第2s内猴子的速度变化量不同 D.t=2s时猴子离出发点的距离为16m
考点四:两个变速直线运动的合成
【例4】为了抗击病毒疫情,保障百姓基本生活,许多快递公司推出了“无接触配送”。快递小哥想到了用无人机配送快递的方法。某次配送快递无人机在飞行过程中,水平方向速度及竖直方向与飞行时间t的关系图像如图甲、图乙所示。关于无人机运动说法正确的是( )
A.时间内,无人机做曲线运动
B.t2时刻,无人机运动到最高点
C. 时间内,无人机做匀变速直线运动
D. 时刻,无人机的速度为
【变式练习】
1.某质点在平面上运动,其在x轴方向和y轴方向上的图像分别如图甲和图乙所示。则下列判断正确的是( )
A.该质点的初速度为 B.前内质点的位移为
C.该质点做匀变速曲线运动 D.该质点有恒定的加速度,大小为
2.为保障灾民生命财产安全,消防队员利用无人机为灾民配送物资,某次在执行任务时,无人机从地面起飞,将配送物资运输到预定地点,在飞行过程中,通过速度传感器测出无人机水平方向和竖直方向的分速度vx和随飞行时间t的关系图像如图甲、乙所示,无人机到达最大高度后释放物资,物资落在预定地点,不计空气阻力,g取10m/s2,以下说法正确的是( )
A.在0~10s内,无人机做曲线运动
B.30s时无人机速度为10m/s
C.25s时无人机加速度大小为0.3m/s2
D.20s时物资从无人机上释放
考点五:小船过河问题
【例5】如图所示,河宽L=200m,河水的流速大小为3m/s。一小船在静水中的速度4m/s,小船自A处出发,渡河时,船头始终垂直河岸方向,到达对岸B处。下列说法正确的是( )
A.小船渡河时间为40s
B.B点在A点下游120m
C.A、B两点间距离为250m
D.无论船头朝向何处,小船都不可以到达A点正对岸
【变式练习】
1.如图所示,一条小船从码头A过河,小船在静水中的速度为v,船头指向始终与河岸垂直(沿AA'方向)。当水流速度为时,小船运动到河对岸的码头B靠岸,AB与河岸的夹角为。当水流速度为时,小船运动到河对岸的码头C靠岸,AC与河岸的夹角为。下列说法正确的是( )
A.小船沿AB、AC过河的时间相等
B.小船沿AC过河的时间更长
C.
D.当水流速度为时,要使小船到达码头,船头应指向河的上游且与河岸夹角为
2.一艘小船在静水中的速度大小为4m/s,河宽100m,河水流速大小为5m/s。则小船( )
A.运动的最大速度是4m/s B.运动的最小速度是3m/s
C.渡河的最短时间是25s D.渡河的最小位移是100m
一、运动的合成与分解
1.合运动与分运动
(1)如果物体同时参与了几个运动,那么物体实际发生的运动就是合运动,参与的几个运动就是分运动.
(2)物体实际运动的位移、速度、加速度是它的合位移、合速度、合加速度,而分运动的位移、速度、加速度就是它的分位移、分速度、分加速度.
2.合运动与分运动的四个特性
等时性 各分运动与合运动同时发生和结束,时间相同
等效性 各分运动的共同效果与合运动的效果相同
同体性 各分运动与合运动是同一物体的运动
独立性 各分运动之间互不相干,彼此独立,互不影响
3.运动的合成与分解
(1)运动的合成与分解是指位移、速度、加速度的合成与分解.其合成、分解遵循平行四边形定则.
(2)对速度v进行分解时,不能随意分解,应按物体的实际运动效果进行分解.
二、合运动的性质与运动轨迹
1.分析两个互成角度的直线运动的合运动的性质时,应先求出合运动的合初速度v和合加速度a,然后进行判断.
(1)是否为匀变速的判断:
加速度或合力
(2)曲、直判断:
加速度或合力与速度方向
2.两个互成角度的直线运动的合运动轨迹的判断:
轨迹在合初速度v0与合加速度a之间,且向加速度一侧弯曲.
一、单选题
1.如图,商场内某顾客站在自动扶梯上随扶梯一起上行,扶梯与水平面夹角为,速度为,将速度沿水平和竖直方向分解,则顾客在竖直方向的分速度为( )
A. B. C. D.
2.如图所示,在一端封闭的光滑细玻璃管中注满清水,水中放一红蜡块R(R可视为质点)。将玻璃管的开口端用胶塞塞紧后竖直倒置且与y轴重合,R从坐标原点开始运动的轨迹如图所示,则红蜡块R在x轴、y轴方向的运动情况可能是( )
A.x轴方向匀速直线运动,y轴方向匀速直线运动
B.x轴方向匀速直线运动,y轴方向匀加速直线运动
C.x轴方向匀减速直线运动,y轴方向匀速直线运动
D.x轴方向匀加速直线运动,y轴方向匀速直线运动
3.如图所示,水平地面上固定一个与水平面夹角为θ的斜杆A,另一竖直直杆B以速度v水平向左做匀速直线运动,所有接触点均光滑。在B杆运动的过程中,两杆交点P的速度大小为( )
A. B. C.v cos θ D.v sin θ
4.小船以一定的速率垂直河岸向对岸划去,当水流匀速时,它渡河的时间、发生的位移与水速的关系是( )
A.水速小时,位移小,时间亦小 B.水速大时,位移大,时间亦大
C.水速大时,位移大,但时间不变 D.位移、时间大小与水速大小无关
5.如图所示,一玻璃管中注满清水,水中放一软木做成的小圆柱体,其直径略小于玻璃管的直径,轻重大小适宜,使它在水中能匀速上浮。将玻璃管的开口端用胶塞塞紧,如图甲,现将玻璃管倒置,如图乙,在小圆柱体上升的同时,使玻璃管水平向右匀加速移动,经过一段时间,玻璃管移至图丙中虚线所示位置,且小圆柱体恰好运动到玻璃管的顶端。在下面四个图中,能正确反映小圆柱体运动轨迹的是( )
A. B.
C. D.
6.如图所示,河水流速以及渡船在静水中的划行速度大小均恒定,渡船从平直河岸边的A处开始渡河,当船头方向垂直河岸时,渡船到达正对岸岸边B处下游的C处,A、C连线与水流方向的夹角为60°。若要使渡船从A处开始渡河,能够沿直线到达B处,则船头方向与水流反方向的夹角θ的正切值应为( )
A. B. C. D.
7.洪涝灾害常常给我们国家带来巨大的经济损失,如图所示某救援队利用摩托艇将人员进行转移。已知水的流速恒为,水流的方向平行于河岸,摩托艇的速度恒为,河宽为。该救援队由河岸的P点出发,将被困人员转移到河对岸,连线与河岸垂直。则下列说法正确的是( )
A.如果,摩托艇可能到达Q
B.摩托艇运动到河对岸时的速度一定大于
C.摩托艇渡河的最短时间为
D.若摩托艇能到达Q,则渡河时间为
8.如图所示,一艘走私船在岸边A点,以速度v0匀速地沿垂直于岸的方向逃跑,距离A点为处的B点的快艇同时启动追击,快艇的速率u大小恒定,方向总是指向走私船,恰好在距岸边的距离为a处逮住走私船,那么以下关于快艇速率的结论正确的是( )
A.快艇在垂直岸边的方向上的平均速度uy=v0
B.快艇在沿岸的方向上的平均速度ux=v0
C.快艇平均速度的大小
D.快艇的平均速率等于
二、多选题
9.如图所示,甲、乙两船在同一条河流中同时开始渡河,河宽,、分别是甲、乙两船的出发点,两船头与河岸均成角,甲船船头恰好对准点的正对岸点,经过一段时间乙船恰好到达点,如果划船速度均为,且两船相遇不影响各自的航行。下列判断正确的是( )
A.水流方向向左,大小为
B.两船同时到达河对岸,花费时间均为
C.甲船水平位移为
D.甲乙两船会在上某点相遇
10.有关运动的合成,以下说法正确的是( )
A.两个直线运动的合运动一定是直线运动
B.两个不在一条直线上的匀速直线运动的合运动一定是直线运动
C.两个初速度为零的匀加速(加速度大小不相等)直线运动的合运动一定是匀加速直线运动
D.匀加速运动和匀速直线运动的合运动一定是直线运动
11.先后将小球1、2由同一位置以不同的速度竖直向上抛出,抛出后小球只受重力和水平方向的风力作用,两小球的运动轨迹如图虚线所示,则两小球相比,下列说法正确的是( )
A.小球1的竖直向上抛出的初速度比2大
B.小球1从抛出到落地的运动时间比2短
C.小球2的水平方向上的平均速度一定比小球1的大
D.小球2所受的风力一定比小球1受到的大
三、实验题
12.冬奥会赛场利用了“高速运动目标跟踪拍摄系统”,不仅让观众看清了动作,还实现了对物体运动情况的多角度定量分析。
为观测冰球在不同方向上的运动情况,冰球场中用三台摄像机进行跟随拍摄,以记录冰球运动的时间、位置等信息。如图所示,在冰面上建立平面直角坐标系,其中设备A视角是竖直向下的,跟随冰球俯拍:设备B、C视角是水平的,分别沿x、y轴跟随拍摄,可以拍摄小球沿x轴、y轴的运动情况。
(1)对设备B拍摄的信息进行分析,得到以下数据,请在答题卡对应方格纸中作出冰球位置随时间变化的图像:
时刻 0 0.4 0.8 1.2 1.6 2.0
位置 0 8.0 16.0 23.8 32.1 39.8
(2)由设备B得到冰球速度大小是____________;
(3)同时,设备C得到冰球的速度大小为,设备A得到冰球的速度大小为。由此可以得出、、之间的数学关系式是____________;
(4)在某次比赛中,B、C设备测出的冰球的速度大小分别是和,则冰球实际运动速度的大小是______________,方向是____________(用实际速度与x轴的夹角的正切值表示)。
四、解答题
13.小船要横渡一条d=200m宽的河,水流速度为v水=4m/s,船在静水中的航速是v船=5m/s,求:
(1)要使小船渡河时间最短,渡河时间是多少?位移大小是多少?
(2)要使小船渡河位移最短,船头应指向何处?多长时间能到达对岸?
5.2 运动的合成与分解
一、一个平面运动的实例——观察蜡块的运动
1.建立坐标系
研究蜡块在平面内的运动,可以选择建立 .
如图所示,以蜡块开始匀速运动的位置为原点O,以水平向右的方向和竖直向上的方向分别为x轴和y轴的方向,建立平面直角坐标系.
2.蜡块运动的位置:玻璃管向右匀速平移的速度设为vx,蜡块沿玻璃管匀速上升的速度设为vy,在某时刻t,蜡块的位置P的坐标:x= ,y= .
3.蜡块运动的轨迹:将x、y消去t,得到y= ,可见蜡块的运动轨迹是一条过原点的直线.
4.蜡块运动的速度:大小v= ,方向满足tan θ= .
二、运动的合成与分解
1.合运动与分运动
如果物体同时参与了几个运动,那么物体实际发生的运动就是 ,同时参与的几个运动就是 .
2.运动的合成与分解:已知分运动求合运动的过程,叫作运动的 ;已知合运动求分运动的过程,叫作运动的 .
3.运动的合成与分解遵循 运算法则.
【参考答案】平面直角坐标系 vxt vyt x 合运动 分运动 合成 分解 矢量
考点一:研究蜡块运动的分解
【例1】红蜡块R可在竖直放置、两端封闭、充满清水的玻璃管中匀速上升。在红蜡块沿玻璃管匀速上升的同时,将玻璃管沿水平方向运动,以蜡块开始运动的位置为原点O,以水平向右的方向和竖直向上的方向分别为x轴和y轴的方向,如图所示,关于红蜡块的运动说法正确的是( )
A.若玻璃管沿x轴正方向做匀速直线运动,红蜡块的运动轨迹一定是直线
B.无论玻璃管沿x轴正方向做何种运动,红蜡块的运动轨迹一定是直线
C.若玻璃管沿x轴正方向做匀加速直线运动,红蜡块速度的大小可能不变
D.若玻璃管沿x轴正方向做匀加速直线运动,红蜡块上升到顶端的时间会变长
【答案】A
【解析】A.由题意可知红蜡块在y轴正方向做匀速直线运动,若玻璃管沿x轴正方向做匀速直线运动,则红蜡块的合运动一定为匀速直线运动,运动轨迹一定是直线,故A正确;BCD.若玻璃管沿x轴正方向做匀加速直线运动,则红蜡块的合运动为匀变速曲线运动,运动轨迹一定是曲线,根据
可知速度大小一定变化,但由于红蜡块在竖直方向上的分速度不变,所以上升到顶端的时间不变,故BCD错误。故选A。
【变式练习】
1.在研究运动的合成与分解时,某同学用红蜡块的运动来进行实验,如图所示,红蜡块在长约为1m的玻璃管中从底部沿竖直方向向上做匀速直线运动,同时该同学拿着玻璃管由静止沿水平方向向右做匀加速直线运动,则该过程中关于红蜡块运动情况的描述正确的是( )
A. B.
C. D.
【答案】C
【解析】蜡烛参与水平向右的匀加速直线运动和竖直向上的匀速直线运动,合加速度的方向水平向右,合初速度方向与合加速度方向不在同一条直线上,必然做曲线运动,根据轨迹每点的切线方向表示速度的方向,轨迹的弯曲的方向大致与所受合力的方向一致,故 C正确,ABD错误。故选C。
2.竖直放置的封闭玻璃管内注满清水,内部有一个红蜡块。玻璃管倒置时蜡块以3m/s的速度向上匀速运动。在蜡块上升的同时,玻璃管以4m/s的速度水平向右运动,如图所示,此时蜡块实际运动的速度大小是( )
A.5m/s B.6m/s C.7m/s D.8m/s
【答案】A
【解析】竖直方向与水平方向的运动是蜡块的分运动,则蜡块的合速度为
故选A。
考点二:互成角度的两个匀速直线运动的合成
【例2】骑射项目是运动会上常见的一种娱乐项目,运动员骑在奔驰的马背上,弯弓射箭射击侧向的靶子目标M,其运动模型简化为如图所示的情境,假设运动员沿方向骑马的速度为,运动员静止时射出的弓箭速度为,直线跑道离固定目标M的最近距离为,假设运动员射箭位置与靶子等高,且垂直跑道方向射出弓箭。不计空气阻力和弓箭的重力,则运动员射出弓箭点的位置距离O点的距离x为( )
A. B. C. D.
【答案】B
【解析】弓箭沿方向和垂直于方向均做匀速直线运动,有
,
可知射出点在O点左侧,且到O点的距离为
故选B。
【变式练习】
1.小船过河时,垂直河岸方向的分速度为4m/s,沿河岸方向的分速度为3m/s,如图所示,小船过河的实际速度大小为( )
A.3m/s B.4m/s C.5m/s D.7m/s
【答案】C
【解析】根据平行四边形定则可知,小船过河的实际速度大小为
故选C。
2.春节期间人们放飞孔明灯表达对新年的祝福,如图所示,若孔明灯在竖直方向做匀速运动,在水平方向做匀速运动,孔明灯的运动轨迹可能为( )
A.直线 B.直线 C.曲线 D.曲线
【答案】B
【解析】孔明灯在竖直Oy方向做匀速运动,水平Ox方向做匀速运动,加速度为零,合力为零,因此孔明灯的运动轨迹可能为图中直线。故选B。
考点三:一个匀速和一个变速运动的合成
【例3】某研究性学习小组为了研究运动的合成与分解,利用图甲所示装置做了如下实验:在一端封闭、长约1m的均匀长直玻璃管内注满清水,水中放一个蜡块,将玻璃管的开口端用胶塞塞紧,然后将这个玻璃管倒置,蜡块能在玻璃管中以的速度匀速上升。若在蜡块上升的同时水平向右移动玻璃管,用y轴表示蜡块竖直方向的位移,x轴表示蜡块随玻璃管通过的水平位移,时刻蜡块位于坐标原点,描出蜡块的运动轨迹如图乙所示。下列说法正确的是( )
A.玻璃管向右匀速平移
B.蜡块做匀变速运动
C.蜡块所受合外力的方向沿图线的切线方向
D.时蜡块的速度大小为20cm/s
【答案】B
【解析】A.蜡块在玻璃管中以的速度匀速上升,由题图乙可知,从t=0时刻起,每1s内玻璃管通过的水平位移依次是2.5cm、7.5cm、12.5cm、17.5cm,可知玻璃管水平向右匀加速平移,选项A错误;
B.蜡块沿水平方向的加速度大小恒定,由运动学公式可知,水平方向的加速度大小为
所以蜡块做匀变速运动,选项B正确;C.做曲线运动的物体所受合外力方向指向轨迹内侧,选项C错误;D.由以上分析和速度的合成可知,t=2s时蜡块的速度大小为
选项D错误。故选B。
【变式练习】
1.方老师用装有水的玻璃管做“观察蜡块的运动”实验时,用气泡代替了蜡块,将玻璃管迅速倒置后,气泡沿着玻璃管加速上升,同时将玻璃管紧贴着黑板沿水平方向向右匀速移动,则气泡的实际运动轨迹可能为( )
A. B.
C. D.
【答案】B
【解析】A.由气泡加速上升,沿水平方向向右匀速移动可知气泡所受合力方向竖直向上,其合速度方向斜右上方,作图如下
故B正确,ACD错误。故选B。
2.在一次杂技表演中,表演者顶着杆沿水平地面运动,其x-t图像如图甲所示。与此同时猴子沿竖直杆向上运动,如图乙所示,其v-t图像如图丙所示,若以地面为参考系,下列说法中正确的是( )
A.猴子的运动轨迹为直线 B.t=1s时猴子的加速度大小为
C.第1s内和第2s内猴子的速度变化量不同 D.t=2s时猴子离出发点的距离为16m
【答案】B
【解析】A.由题意可知猴子在水平方向做匀速直线运动,在竖直方向做匀减速直线运动,其合运动为曲线运动,运动轨迹应为开口向下的抛物线的半支,故A错误;B.t=1s时猴子的加速度大小为
故B正确;C.猴子做匀变速曲线运动,第1s内和第2s内猴子的速度变化量相同,故C错误;D.t=2s时,猴子在水平和竖直方向的位移大小分别为
此时猴子离出发点的距离为
故D错误。故选B。
考点四:两个变速直线运动的合成
【例4】为了抗击病毒疫情,保障百姓基本生活,许多快递公司推出了“无接触配送”。快递小哥想到了用无人机配送快递的方法。某次配送快递无人机在飞行过程中,水平方向速度及竖直方向与飞行时间t的关系图像如图甲、图乙所示。关于无人机运动说法正确的是( )
A.时间内,无人机做曲线运动
B.t2时刻,无人机运动到最高点
C. 时间内,无人机做匀变速直线运动
D. 时刻,无人机的速度为
【答案】D
【解析】A.0~t1时间内,无人机在水平方向做初速度为零的匀加速运动,在竖直方向也做初速度为零的匀加速运动,则合运动为匀加速直线运动,选项A错误;B.时间内,无人机速度一直为正,即一直向上运动,则时刻,无人机还没有运动到最高点,选项B错误;C.时间内,无人机水平方向做速度为的匀速运动,竖直方向做匀减速运动,则合运动为匀变速曲线运动,选项C错误;D.t2时刻,无人机的水平速度为,竖直速度为,则合速度为,选项D正确。故选D。
【变式练习】
1.某质点在平面上运动,其在x轴方向和y轴方向上的图像分别如图甲和图乙所示。则下列判断正确的是( )
A.该质点的初速度为 B.前内质点的位移为
C.该质点做匀变速曲线运动 D.该质点有恒定的加速度,大小为
【答案】D
【解析】根据图像中图线的斜率表示加速度,由图甲可知,质点在在x轴方向上,初速度为
加速度为
由图乙可知,质点在在y轴方向上,初速度为
加速度为
A.根据运动的合成可知,该质点的初速度为
故A错误;CD.根据运动的合成可知,该质点的加速度为
即该质点有恒定的加速度,大小为,设加速度与轴的夹角为,初速度与轴的夹角为,根据几何关系可得
,
即质点的初速度与加速度方向相同,则质点做匀加速直线运动,故C错误D正确;
B.由于质点做匀加速直线运动,由运动学公式可得,前内质点的位移为
故B错误。故选D。
2.为保障灾民生命财产安全,消防队员利用无人机为灾民配送物资,某次在执行任务时,无人机从地面起飞,将配送物资运输到预定地点,在飞行过程中,通过速度传感器测出无人机水平方向和竖直方向的分速度vx和随飞行时间t的关系图像如图甲、乙所示,无人机到达最大高度后释放物资,物资落在预定地点,不计空气阻力,g取10m/s2,以下说法正确的是( )
A.在0~10s内,无人机做曲线运动
B.30s时无人机速度为10m/s
C.25s时无人机加速度大小为0.3m/s2
D.20s时物资从无人机上释放
【答案】B
【解析】A.0~10s时间内,无人机在水平方向上做初速度为零的匀加速运动,在竖直方向上做初速度为零的匀加速运动,则合运动为初速为零的匀加速直线运动,故A错误;
B.30s时刻无人机水平方向速度,竖直方向上速度,此时速度
故B正确;C.25s时无人机水平方向加速度为零,竖直方向加速度即为无人机的加速度,其大小为
故C错误;D.0~40s时间内无人机竖直方向上速度均向上,一直升高,无人机到达最大高度后释放物资,故40s时物资从无人机上释放,故D错误。故选B。
考点五:小船过河问题
【例5】如图所示,河宽L=200m,河水的流速大小为3m/s。一小船在静水中的速度4m/s,小船自A处出发,渡河时,船头始终垂直河岸方向,到达对岸B处。下列说法正确的是( )
A.小船渡河时间为40s
B.B点在A点下游120m
C.A、B两点间距离为250m
D.无论船头朝向何处,小船都不可以到达A点正对岸
【答案】C
【解析】A.渡河时,船头始终垂直河岸方向,则小船渡河时间
故A错误;B.船随水漂流
x=vst=3×50m=150m
即B点在A点下游150m,故B错误;C.根据平行四边形定则可知,A、B两点间距离
故C正确;D.分析可知,小船在静水中的速度大于河水的流速,当合速度与河岸垂直,小船到达正对岸,设静水中速度的方向与河岸的夹角为θ
当θ满足上述条件时,小船可以到达A点正对岸,故D错误。故选C。
【变式练习】
1.如图所示,一条小船从码头A过河,小船在静水中的速度为v,船头指向始终与河岸垂直(沿AA'方向)。当水流速度为时,小船运动到河对岸的码头B靠岸,AB与河岸的夹角为。当水流速度为时,小船运动到河对岸的码头C靠岸,AC与河岸的夹角为。下列说法正确的是( )
A.小船沿AB、AC过河的时间相等
B.小船沿AC过河的时间更长
C.
D.当水流速度为时,要使小船到达码头,船头应指向河的上游且与河岸夹角为
【答案】A
【解析】AB.因船头始终垂直于河岸,可知船过河的时间为
即小船沿AB、AC过河的时间相等,选项A正确,B错误;C.由题意可知
解得
选项C错误;
D.当水流速度为时,要使小船到达码头,则合速度应该垂直河对岸,船头应指向河的上游且与河岸夹角为
则
选项D错误。故选A。
2.一艘小船在静水中的速度大小为4m/s,河宽100m,河水流速大小为5m/s。则小船( )
A.运动的最大速度是4m/s B.运动的最小速度是3m/s
C.渡河的最短时间是25s D.渡河的最小位移是100m
【答案】C
【解析】AB.当船行驶方向与水流速同向,小船速度最大,为
当船行驶方向与水流速反向,小船速度最小,为
故AB错误;C.当静水速与河岸垂直时,渡河时间最短
故C正确;D.因为静水速小于水流速,可知合速度的方向不可能垂直于河岸,则小船不能垂直到对岸,最小距离不会等于100m,要大于100m,故D错误。故选C。
一、运动的合成与分解
1.合运动与分运动
(1)如果物体同时参与了几个运动,那么物体实际发生的运动就是合运动,参与的几个运动就是分运动.
(2)物体实际运动的位移、速度、加速度是它的合位移、合速度、合加速度,而分运动的位移、速度、加速度就是它的分位移、分速度、分加速度.
2.合运动与分运动的四个特性
等时性 各分运动与合运动同时发生和结束,时间相同
等效性 各分运动的共同效果与合运动的效果相同
同体性 各分运动与合运动是同一物体的运动
独立性 各分运动之间互不相干,彼此独立,互不影响
3.运动的合成与分解
(1)运动的合成与分解是指位移、速度、加速度的合成与分解.其合成、分解遵循平行四边形定则.
(2)对速度v进行分解时,不能随意分解,应按物体的实际运动效果进行分解.
二、合运动的性质与运动轨迹
1.分析两个互成角度的直线运动的合运动的性质时,应先求出合运动的合初速度v和合加速度a,然后进行判断.
(1)是否为匀变速的判断:
加速度或合力
(2)曲、直判断:
加速度或合力与速度方向
2.两个互成角度的直线运动的合运动轨迹的判断:
轨迹在合初速度v0与合加速度a之间,且向加速度一侧弯曲.
一、单选题
1.如图,商场内某顾客站在自动扶梯上随扶梯一起上行,扶梯与水平面夹角为,速度为,将速度沿水平和竖直方向分解,则顾客在竖直方向的分速度为( )
A. B. C. D.
【答案】B
【解析】根据几何关系可知
解得
故选B。
2.如图所示,在一端封闭的光滑细玻璃管中注满清水,水中放一红蜡块R(R可视为质点)。将玻璃管的开口端用胶塞塞紧后竖直倒置且与y轴重合,R从坐标原点开始运动的轨迹如图所示,则红蜡块R在x轴、y轴方向的运动情况可能是( )
A.x轴方向匀速直线运动,y轴方向匀速直线运动
B.x轴方向匀速直线运动,y轴方向匀加速直线运动
C.x轴方向匀减速直线运动,y轴方向匀速直线运动
D.x轴方向匀加速直线运动,y轴方向匀速直线运动
【答案】D
【解析】AB.若x轴方向匀速直线运动,根据运动轨迹的形状,则y轴方向的加速度方向沿y轴负方向,即y轴方向减速直线运动。故AB错误;CD.若y轴方向匀速直线运动,根据运动轨迹的形状,则x轴方向的加速度方向沿x轴正方向,即x轴方向加速直线运动。故C错误;D正确。故选D。
3.如图所示,水平地面上固定一个与水平面夹角为θ的斜杆A,另一竖直直杆B以速度v水平向左做匀速直线运动,所有接触点均光滑。在B杆运动的过程中,两杆交点P的速度大小为( )
A. B. C.v cos θ D.v sin θ
【答案】A
【解析】两杆的交点P参与了两个分运动:与B杆一起以速度v水平向左的匀速直线运动和沿B杆竖直向上的运动,交点P的实际运动方向沿A杆斜向上,如图所示,则交点P的速度大小为
故A正确BCD错误。故选A。
4.小船以一定的速率垂直河岸向对岸划去,当水流匀速时,它渡河的时间、发生的位移与水速的关系是( )
A.水速小时,位移小,时间亦小 B.水速大时,位移大,时间亦大
C.水速大时,位移大,但时间不变 D.位移、时间大小与水速大小无关
【答案】C
【解析】小船以一定的速率使船头垂直河岸向对岸划去,即垂直于河岸方向上的速度不变,根据
知水流速变化时,渡河的时间不变,水流速增大,则
在沿河岸方向上的位移增大,则合位移增大。故选C。
5.如图所示,一玻璃管中注满清水,水中放一软木做成的小圆柱体,其直径略小于玻璃管的直径,轻重大小适宜,使它在水中能匀速上浮。将玻璃管的开口端用胶塞塞紧,如图甲,现将玻璃管倒置,如图乙,在小圆柱体上升的同时,使玻璃管水平向右匀加速移动,经过一段时间,玻璃管移至图丙中虚线所示位置,且小圆柱体恰好运动到玻璃管的顶端。在下面四个图中,能正确反映小圆柱体运动轨迹的是( )
A. B.
C. D.
【答案】C
【解析】小圆柱体竖直向上做匀速直线运动,水平向右做初速度为零的匀加速直线运动,则
联立解得
(其中,)
故选C。
6.如图所示,河水流速以及渡船在静水中的划行速度大小均恒定,渡船从平直河岸边的A处开始渡河,当船头方向垂直河岸时,渡船到达正对岸岸边B处下游的C处,A、C连线与水流方向的夹角为60°。若要使渡船从A处开始渡河,能够沿直线到达B处,则船头方向与水流反方向的夹角θ的正切值应为( )
A. B. C. D.
【答案】A
【解析】设船在静水中的速度为v1,水速为v2,则
当船垂直渡河时
得
故选A。
7.洪涝灾害常常给我们国家带来巨大的经济损失,如图所示某救援队利用摩托艇将人员进行转移。已知水的流速恒为,水流的方向平行于河岸,摩托艇的速度恒为,河宽为。该救援队由河岸的P点出发,将被困人员转移到河对岸,连线与河岸垂直。则下列说法正确的是( )
A.如果,摩托艇可能到达Q
B.摩托艇运动到河对岸时的速度一定大于
C.摩托艇渡河的最短时间为
D.若摩托艇能到达Q,则渡河时间为
【答案】C
【解析】A.如果,摩托艇的合速度方向不可能垂直于河岸,所以摩托艇不可能到达Q,故A错误;B.若满足,则摩托艇的合速度方向可以垂直于河岸,当摩托艇以垂直河岸的合速度方向到达对岸时,摩托艇的合速度大小为
故B错误;C.当摩托艇分速度垂直于河岸时,渡河时间最短,则有
故C正确;D.若摩托艇能到达Q,则摩托艇的合速度方向垂直于河岸,此时合速度大小为
渡河时间为
故D错误。故选C。
8.如图所示,一艘走私船在岸边A点,以速度v0匀速地沿垂直于岸的方向逃跑,距离A点为处的B点的快艇同时启动追击,快艇的速率u大小恒定,方向总是指向走私船,恰好在距岸边的距离为a处逮住走私船,那么以下关于快艇速率的结论正确的是( )
A.快艇在垂直岸边的方向上的平均速度uy=v0
B.快艇在沿岸的方向上的平均速度ux=v0
C.快艇平均速度的大小
D.快艇的平均速率等于
【答案】A
【解析】A.从开始到追及的过程中,由于在垂直岸边的方向上,两船和快艇的位移及经历的时间相同,所以快艇在垂直于岸边的方向上的平均速度等于走私船的速度,即
uy=v0
故A正确;B.由快艇在沿河岸方向上的位移
与垂直于河岸方向上的位移
a=uyt
可知,快艇在沿岸边的方向上的平均速度为
故B错误;C.快艇发生的位移
再结合l=ut可得快艇的平均速度大小为
故C错误;
D.由于快艇运动中速度方向不停地变化,即快艇做曲线运动,则快艇通过的路程一定大于其位移 ,故平均速率一定大于 ,故D错误。故选A。
二、多选题
9.如图所示,甲、乙两船在同一条河流中同时开始渡河,河宽,、分别是甲、乙两船的出发点,两船头与河岸均成角,甲船船头恰好对准点的正对岸点,经过一段时间乙船恰好到达点,如果划船速度均为,且两船相遇不影响各自的航行。下列判断正确的是( )
A.水流方向向左,大小为
B.两船同时到达河对岸,花费时间均为
C.甲船水平位移为
D.甲乙两船会在上某点相遇
【答案】BD
【解析】A.以乙船为研究对象,如果水流方向向左,则如图1所示
则船的合速度方向为左斜向上,不可能会到达P点,则说明水流方向一定向右,且依题意乙船的合速度垂直对岸,则船向左的分速度与水流速度相抵消,可得
故A错误;B.两船在与垂直水流方向上的速度均为,且河宽均为d,则两船同时到达河对岸,根据运动的独立性,可知花费时间均为
故B正确;C.以甲船为研究对象,水流方向向右,则如图2所示
则船在水平方向上的速度为
则甲船水平位移为
故C错误;D.甲乙两船在纵向上的速度均为,且这也是乙的合速度,而甲船还有横向速度,相当于两船在纵向上相对静止,而横向上甲船以的水平速度靠近乙船,所以甲乙两船会在PN上某点相遇,故D正确。故选BD。
10.有关运动的合成,以下说法正确的是( )
A.两个直线运动的合运动一定是直线运动
B.两个不在一条直线上的匀速直线运动的合运动一定是直线运动
C.两个初速度为零的匀加速(加速度大小不相等)直线运动的合运动一定是匀加速直线运动
D.匀加速运动和匀速直线运动的合运动一定是直线运动
【答案】BC
【解析】B.选项中对两个直线运动的速度没有要求,可设初速度分别为、,如图所示
若两分运动为不在同一直线上的匀速直线运动,则根据平行四边形定则可得恒定,即做匀速直线运动,B正确;AD.若两分运动有加速度,还需把加速度合成,其加速度若与同向则加速,若与反向则减速,若与不在同一直线上则做曲线运动,AD错误;C.若两分运动的初速度均为零,则合运动为匀加速直线运动,C正确。故选BC。
11.先后将小球1、2由同一位置以不同的速度竖直向上抛出,抛出后小球只受重力和水平方向的风力作用,两小球的运动轨迹如图虚线所示,则两小球相比,下列说法正确的是( )
A.小球1的竖直向上抛出的初速度比2大
B.小球1从抛出到落地的运动时间比2短
C.小球2的水平方向上的平均速度一定比小球1的大
D.小球2所受的风力一定比小球1受到的大
【答案】AC
【解析】AB.小球的运动可以分解为竖直方向的竖直上抛和水平方向的匀加速直线运动,上升阶段竖直方向满足
依题意,可知小球1上升高度大于小球2的上升高度,所以小球1竖直向上抛出的初速度大,小球1从抛出到落地的运动时间长,故A正确,B错误;C.由图可知,小球1水平位移小,飞行时间长,根据水平方向的平均速度
分析知小球2的水平方向的平均速度一定比小球1的大,故C正确;D.小球水平方向满足
由图可知,小球1的飞行时间长,水平位移小,小球1的加速度小,但不知道两小球质量的关系,故不能判断出二者水平方向受力的关系,故D错误。故选AC。
三、实验题
12.冬奥会赛场利用了“高速运动目标跟踪拍摄系统”,不仅让观众看清了动作,还实现了对物体运动情况的多角度定量分析。
为观测冰球在不同方向上的运动情况,冰球场中用三台摄像机进行跟随拍摄,以记录冰球运动的时间、位置等信息。如图所示,在冰面上建立平面直角坐标系,其中设备A视角是竖直向下的,跟随冰球俯拍:设备B、C视角是水平的,分别沿x、y轴跟随拍摄,可以拍摄小球沿x轴、y轴的运动情况。
(1)对设备B拍摄的信息进行分析,得到以下数据,请在答题卡对应方格纸中作出冰球位置随时间变化的图像:
时刻 0 0.4 0.8 1.2 1.6 2.0
位置 0 8.0 16.0 23.8 32.1 39.8
(2)由设备B得到冰球速度大小是____________;
(3)同时,设备C得到冰球的速度大小为,设备A得到冰球的速度大小为。由此可以得出、、之间的数学关系式是____________;
(4)在某次比赛中,B、C设备测出的冰球的速度大小分别是和,则冰球实际运动速度的大小是______________,方向是____________(用实际速度与x轴的夹角的正切值表示)。
【答案】(2)19.9 (3) (4)17
【解析】(2)[1] 由设备B得到冰球速度大小是
(3)[2] 同时,设备C得到冰球的速度大小为,设备A得到冰球的速度大小为。由此可以得出、、之间的数学关系式是
(4)[3] 在某次比赛中,B、C设备测出的冰球的速度大小分别是和,则冰球实际运动速度的大小是
[4] 设实际速度与x轴的夹角为,则
四、解答题
13.小船要横渡一条d=200m宽的河,水流速度为v水=4m/s,船在静水中的航速是v船=5m/s,求:
(1)要使小船渡河时间最短,渡河时间是多少?位移大小是多少?
(2)要使小船渡河位移最短,船头应指向何处?多长时间能到达对岸?
【答案】(1)40s,;(2)船头与上游河岸的夹角为,
【解析】(1)要使小船渡河时间最短,船头要垂直河岸,如图1所示
渡河时间为
合速度为
位移大小为
(2)由于船速大于水速,当合速度垂直于河岸时,位移最短,如图2所示
设船头与上游河岸的夹角为,则
则
所以要使小船渡河位移最短,船头与上游河岸的夹角为。
合速度大小为
到达对岸时间为
一、一个平面运动的实例——观察蜡块的运动
1.建立坐标系
研究蜡块在平面内的运动,可以选择建立 .
如图所示,以蜡块开始匀速运动的位置为原点O,以水平向右的方向和竖直向上的方向分别为x轴和y轴的方向,建立平面直角坐标系.
2.蜡块运动的位置:玻璃管向右匀速平移的速度设为vx,蜡块沿玻璃管匀速上升的速度设为vy,在某时刻t,蜡块的位置P的坐标:x= ,y= .
3.蜡块运动的轨迹:将x、y消去t,得到y= ,可见蜡块的运动轨迹是一条过原点的直线.
4.蜡块运动的速度:大小v= ,方向满足tan θ= .
二、运动的合成与分解
1.合运动与分运动
如果物体同时参与了几个运动,那么物体实际发生的运动就是 ,同时参与的几个运动就是 .
2.运动的合成与分解:已知分运动求合运动的过程,叫作运动的 ;已知合运动求分运动的过程,叫作运动的 .
3.运动的合成与分解遵循 运算法则.
考点一:研究蜡块运动的分解
【例1】红蜡块R可在竖直放置、两端封闭、充满清水的玻璃管中匀速上升。在红蜡块沿玻璃管匀速上升的同时,将玻璃管沿水平方向运动,以蜡块开始运动的位置为原点O,以水平向右的方向和竖直向上的方向分别为x轴和y轴的方向,如图所示,关于红蜡块的运动说法正确的是( )
A.若玻璃管沿x轴正方向做匀速直线运动,红蜡块的运动轨迹一定是直线
B.无论玻璃管沿x轴正方向做何种运动,红蜡块的运动轨迹一定是直线
C.若玻璃管沿x轴正方向做匀加速直线运动,红蜡块速度的大小可能不变
D.若玻璃管沿x轴正方向做匀加速直线运动,红蜡块上升到顶端的时间会变长
【变式练习】
1.在研究运动的合成与分解时,某同学用红蜡块的运动来进行实验,如图所示,红蜡块在长约为1m的玻璃管中从底部沿竖直方向向上做匀速直线运动,同时该同学拿着玻璃管由静止沿水平方向向右做匀加速直线运动,则该过程中关于红蜡块运动情况的描述正确的是( )
A. B.
C. D.
2.竖直放置的封闭玻璃管内注满清水,内部有一个红蜡块。玻璃管倒置时蜡块以3m/s的速度向上匀速运动。在蜡块上升的同时,玻璃管以4m/s的速度水平向右运动,如图所示,此时蜡块实际运动的速度大小是( )
A.5m/s B.6m/s C.7m/s D.8m/s
考点二:互成角度的两个匀速直线运动的合成
【例2】骑射项目是运动会上常见的一种娱乐项目,运动员骑在奔驰的马背上,弯弓射箭射击侧向的靶子目标M,其运动模型简化为如图所示的情境,假设运动员沿方向骑马的速度为,运动员静止时射出的弓箭速度为,直线跑道离固定目标M的最近距离为,假设运动员射箭位置与靶子等高,且垂直跑道方向射出弓箭。不计空气阻力和弓箭的重力,则运动员射出弓箭点的位置距离O点的距离x为( )
A. B. C. D.
【变式练习】
1.小船过河时,垂直河岸方向的分速度为4m/s,沿河岸方向的分速度为3m/s,如图所示,小船过河的实际速度大小为( )
A.3m/s B.4m/s C.5m/s D.7m/s
2.春节期间人们放飞孔明灯表达对新年的祝福,如图所示,若孔明灯在竖直方向做匀速运动,在水平方向做匀速运动,孔明灯的运动轨迹可能为( )
A.直线 B.直线 C.曲线 D.曲线
考点三:一个匀速和一个变速运动的合成
【例3】某研究性学习小组为了研究运动的合成与分解,利用图甲所示装置做了如下实验:在一端封闭、长约1m的均匀长直玻璃管内注满清水,水中放一个蜡块,将玻璃管的开口端用胶塞塞紧,然后将这个玻璃管倒置,蜡块能在玻璃管中以的速度匀速上升。若在蜡块上升的同时水平向右移动玻璃管,用y轴表示蜡块竖直方向的位移,x轴表示蜡块随玻璃管通过的水平位移,时刻蜡块位于坐标原点,描出蜡块的运动轨迹如图乙所示。下列说法正确的是( )
A.玻璃管向右匀速平移
B.蜡块做匀变速运动
C.蜡块所受合外力的方向沿图线的切线方向
D.时蜡块的速度大小为20cm/s
【变式练习】
1.方老师用装有水的玻璃管做“观察蜡块的运动”实验时,用气泡代替了蜡块,将玻璃管迅速倒置后,气泡沿着玻璃管加速上升,同时将玻璃管紧贴着黑板沿水平方向向右匀速移动,则气泡的实际运动轨迹可能为( )
A. B.
C. D.
2.在一次杂技表演中,表演者顶着杆沿水平地面运动,其x-t图像如图甲所示。与此同时猴子沿竖直杆向上运动,如图乙所示,其v-t图像如图丙所示,若以地面为参考系,下列说法中正确的是( )
A.猴子的运动轨迹为直线 B.t=1s时猴子的加速度大小为
C.第1s内和第2s内猴子的速度变化量不同 D.t=2s时猴子离出发点的距离为16m
考点四:两个变速直线运动的合成
【例4】为了抗击病毒疫情,保障百姓基本生活,许多快递公司推出了“无接触配送”。快递小哥想到了用无人机配送快递的方法。某次配送快递无人机在飞行过程中,水平方向速度及竖直方向与飞行时间t的关系图像如图甲、图乙所示。关于无人机运动说法正确的是( )
A.时间内,无人机做曲线运动
B.t2时刻,无人机运动到最高点
C. 时间内,无人机做匀变速直线运动
D. 时刻,无人机的速度为
【变式练习】
1.某质点在平面上运动,其在x轴方向和y轴方向上的图像分别如图甲和图乙所示。则下列判断正确的是( )
A.该质点的初速度为 B.前内质点的位移为
C.该质点做匀变速曲线运动 D.该质点有恒定的加速度,大小为
2.为保障灾民生命财产安全,消防队员利用无人机为灾民配送物资,某次在执行任务时,无人机从地面起飞,将配送物资运输到预定地点,在飞行过程中,通过速度传感器测出无人机水平方向和竖直方向的分速度vx和随飞行时间t的关系图像如图甲、乙所示,无人机到达最大高度后释放物资,物资落在预定地点,不计空气阻力,g取10m/s2,以下说法正确的是( )
A.在0~10s内,无人机做曲线运动
B.30s时无人机速度为10m/s
C.25s时无人机加速度大小为0.3m/s2
D.20s时物资从无人机上释放
考点五:小船过河问题
【例5】如图所示,河宽L=200m,河水的流速大小为3m/s。一小船在静水中的速度4m/s,小船自A处出发,渡河时,船头始终垂直河岸方向,到达对岸B处。下列说法正确的是( )
A.小船渡河时间为40s
B.B点在A点下游120m
C.A、B两点间距离为250m
D.无论船头朝向何处,小船都不可以到达A点正对岸
【变式练习】
1.如图所示,一条小船从码头A过河,小船在静水中的速度为v,船头指向始终与河岸垂直(沿AA'方向)。当水流速度为时,小船运动到河对岸的码头B靠岸,AB与河岸的夹角为。当水流速度为时,小船运动到河对岸的码头C靠岸,AC与河岸的夹角为。下列说法正确的是( )
A.小船沿AB、AC过河的时间相等
B.小船沿AC过河的时间更长
C.
D.当水流速度为时,要使小船到达码头,船头应指向河的上游且与河岸夹角为
2.一艘小船在静水中的速度大小为4m/s,河宽100m,河水流速大小为5m/s。则小船( )
A.运动的最大速度是4m/s B.运动的最小速度是3m/s
C.渡河的最短时间是25s D.渡河的最小位移是100m
一、运动的合成与分解
1.合运动与分运动
(1)如果物体同时参与了几个运动,那么物体实际发生的运动就是合运动,参与的几个运动就是分运动.
(2)物体实际运动的位移、速度、加速度是它的合位移、合速度、合加速度,而分运动的位移、速度、加速度就是它的分位移、分速度、分加速度.
2.合运动与分运动的四个特性
等时性 各分运动与合运动同时发生和结束,时间相同
等效性 各分运动的共同效果与合运动的效果相同
同体性 各分运动与合运动是同一物体的运动
独立性 各分运动之间互不相干,彼此独立,互不影响
3.运动的合成与分解
(1)运动的合成与分解是指位移、速度、加速度的合成与分解.其合成、分解遵循平行四边形定则.
(2)对速度v进行分解时,不能随意分解,应按物体的实际运动效果进行分解.
二、合运动的性质与运动轨迹
1.分析两个互成角度的直线运动的合运动的性质时,应先求出合运动的合初速度v和合加速度a,然后进行判断.
(1)是否为匀变速的判断:
加速度或合力
(2)曲、直判断:
加速度或合力与速度方向
2.两个互成角度的直线运动的合运动轨迹的判断:
轨迹在合初速度v0与合加速度a之间,且向加速度一侧弯曲.
一、单选题
1.如图,商场内某顾客站在自动扶梯上随扶梯一起上行,扶梯与水平面夹角为,速度为,将速度沿水平和竖直方向分解,则顾客在竖直方向的分速度为( )
A. B. C. D.
2.如图所示,在一端封闭的光滑细玻璃管中注满清水,水中放一红蜡块R(R可视为质点)。将玻璃管的开口端用胶塞塞紧后竖直倒置且与y轴重合,R从坐标原点开始运动的轨迹如图所示,则红蜡块R在x轴、y轴方向的运动情况可能是( )
A.x轴方向匀速直线运动,y轴方向匀速直线运动
B.x轴方向匀速直线运动,y轴方向匀加速直线运动
C.x轴方向匀减速直线运动,y轴方向匀速直线运动
D.x轴方向匀加速直线运动,y轴方向匀速直线运动
3.如图所示,水平地面上固定一个与水平面夹角为θ的斜杆A,另一竖直直杆B以速度v水平向左做匀速直线运动,所有接触点均光滑。在B杆运动的过程中,两杆交点P的速度大小为( )
A. B. C.v cos θ D.v sin θ
4.小船以一定的速率垂直河岸向对岸划去,当水流匀速时,它渡河的时间、发生的位移与水速的关系是( )
A.水速小时,位移小,时间亦小 B.水速大时,位移大,时间亦大
C.水速大时,位移大,但时间不变 D.位移、时间大小与水速大小无关
5.如图所示,一玻璃管中注满清水,水中放一软木做成的小圆柱体,其直径略小于玻璃管的直径,轻重大小适宜,使它在水中能匀速上浮。将玻璃管的开口端用胶塞塞紧,如图甲,现将玻璃管倒置,如图乙,在小圆柱体上升的同时,使玻璃管水平向右匀加速移动,经过一段时间,玻璃管移至图丙中虚线所示位置,且小圆柱体恰好运动到玻璃管的顶端。在下面四个图中,能正确反映小圆柱体运动轨迹的是( )
A. B.
C. D.
6.如图所示,河水流速以及渡船在静水中的划行速度大小均恒定,渡船从平直河岸边的A处开始渡河,当船头方向垂直河岸时,渡船到达正对岸岸边B处下游的C处,A、C连线与水流方向的夹角为60°。若要使渡船从A处开始渡河,能够沿直线到达B处,则船头方向与水流反方向的夹角θ的正切值应为( )
A. B. C. D.
7.洪涝灾害常常给我们国家带来巨大的经济损失,如图所示某救援队利用摩托艇将人员进行转移。已知水的流速恒为,水流的方向平行于河岸,摩托艇的速度恒为,河宽为。该救援队由河岸的P点出发,将被困人员转移到河对岸,连线与河岸垂直。则下列说法正确的是( )
A.如果,摩托艇可能到达Q
B.摩托艇运动到河对岸时的速度一定大于
C.摩托艇渡河的最短时间为
D.若摩托艇能到达Q,则渡河时间为
8.如图所示,一艘走私船在岸边A点,以速度v0匀速地沿垂直于岸的方向逃跑,距离A点为处的B点的快艇同时启动追击,快艇的速率u大小恒定,方向总是指向走私船,恰好在距岸边的距离为a处逮住走私船,那么以下关于快艇速率的结论正确的是( )
A.快艇在垂直岸边的方向上的平均速度uy=v0
B.快艇在沿岸的方向上的平均速度ux=v0
C.快艇平均速度的大小
D.快艇的平均速率等于
二、多选题
9.如图所示,甲、乙两船在同一条河流中同时开始渡河,河宽,、分别是甲、乙两船的出发点,两船头与河岸均成角,甲船船头恰好对准点的正对岸点,经过一段时间乙船恰好到达点,如果划船速度均为,且两船相遇不影响各自的航行。下列判断正确的是( )
A.水流方向向左,大小为
B.两船同时到达河对岸,花费时间均为
C.甲船水平位移为
D.甲乙两船会在上某点相遇
10.有关运动的合成,以下说法正确的是( )
A.两个直线运动的合运动一定是直线运动
B.两个不在一条直线上的匀速直线运动的合运动一定是直线运动
C.两个初速度为零的匀加速(加速度大小不相等)直线运动的合运动一定是匀加速直线运动
D.匀加速运动和匀速直线运动的合运动一定是直线运动
11.先后将小球1、2由同一位置以不同的速度竖直向上抛出,抛出后小球只受重力和水平方向的风力作用,两小球的运动轨迹如图虚线所示,则两小球相比,下列说法正确的是( )
A.小球1的竖直向上抛出的初速度比2大
B.小球1从抛出到落地的运动时间比2短
C.小球2的水平方向上的平均速度一定比小球1的大
D.小球2所受的风力一定比小球1受到的大
三、实验题
12.冬奥会赛场利用了“高速运动目标跟踪拍摄系统”,不仅让观众看清了动作,还实现了对物体运动情况的多角度定量分析。
为观测冰球在不同方向上的运动情况,冰球场中用三台摄像机进行跟随拍摄,以记录冰球运动的时间、位置等信息。如图所示,在冰面上建立平面直角坐标系,其中设备A视角是竖直向下的,跟随冰球俯拍:设备B、C视角是水平的,分别沿x、y轴跟随拍摄,可以拍摄小球沿x轴、y轴的运动情况。
(1)对设备B拍摄的信息进行分析,得到以下数据,请在答题卡对应方格纸中作出冰球位置随时间变化的图像:
时刻 0 0.4 0.8 1.2 1.6 2.0
位置 0 8.0 16.0 23.8 32.1 39.8
(2)由设备B得到冰球速度大小是____________;
(3)同时,设备C得到冰球的速度大小为,设备A得到冰球的速度大小为。由此可以得出、、之间的数学关系式是____________;
(4)在某次比赛中,B、C设备测出的冰球的速度大小分别是和,则冰球实际运动速度的大小是______________,方向是____________(用实际速度与x轴的夹角的正切值表示)。
四、解答题
13.小船要横渡一条d=200m宽的河,水流速度为v水=4m/s,船在静水中的航速是v船=5m/s,求:
(1)要使小船渡河时间最短,渡河时间是多少?位移大小是多少?
(2)要使小船渡河位移最短,船头应指向何处?多长时间能到达对岸?
5.2 运动的合成与分解
一、一个平面运动的实例——观察蜡块的运动
1.建立坐标系
研究蜡块在平面内的运动,可以选择建立 .
如图所示,以蜡块开始匀速运动的位置为原点O,以水平向右的方向和竖直向上的方向分别为x轴和y轴的方向,建立平面直角坐标系.
2.蜡块运动的位置:玻璃管向右匀速平移的速度设为vx,蜡块沿玻璃管匀速上升的速度设为vy,在某时刻t,蜡块的位置P的坐标:x= ,y= .
3.蜡块运动的轨迹:将x、y消去t,得到y= ,可见蜡块的运动轨迹是一条过原点的直线.
4.蜡块运动的速度:大小v= ,方向满足tan θ= .
二、运动的合成与分解
1.合运动与分运动
如果物体同时参与了几个运动,那么物体实际发生的运动就是 ,同时参与的几个运动就是 .
2.运动的合成与分解:已知分运动求合运动的过程,叫作运动的 ;已知合运动求分运动的过程,叫作运动的 .
3.运动的合成与分解遵循 运算法则.
【参考答案】平面直角坐标系 vxt vyt x 合运动 分运动 合成 分解 矢量
考点一:研究蜡块运动的分解
【例1】红蜡块R可在竖直放置、两端封闭、充满清水的玻璃管中匀速上升。在红蜡块沿玻璃管匀速上升的同时,将玻璃管沿水平方向运动,以蜡块开始运动的位置为原点O,以水平向右的方向和竖直向上的方向分别为x轴和y轴的方向,如图所示,关于红蜡块的运动说法正确的是( )
A.若玻璃管沿x轴正方向做匀速直线运动,红蜡块的运动轨迹一定是直线
B.无论玻璃管沿x轴正方向做何种运动,红蜡块的运动轨迹一定是直线
C.若玻璃管沿x轴正方向做匀加速直线运动,红蜡块速度的大小可能不变
D.若玻璃管沿x轴正方向做匀加速直线运动,红蜡块上升到顶端的时间会变长
【答案】A
【解析】A.由题意可知红蜡块在y轴正方向做匀速直线运动,若玻璃管沿x轴正方向做匀速直线运动,则红蜡块的合运动一定为匀速直线运动,运动轨迹一定是直线,故A正确;BCD.若玻璃管沿x轴正方向做匀加速直线运动,则红蜡块的合运动为匀变速曲线运动,运动轨迹一定是曲线,根据
可知速度大小一定变化,但由于红蜡块在竖直方向上的分速度不变,所以上升到顶端的时间不变,故BCD错误。故选A。
【变式练习】
1.在研究运动的合成与分解时,某同学用红蜡块的运动来进行实验,如图所示,红蜡块在长约为1m的玻璃管中从底部沿竖直方向向上做匀速直线运动,同时该同学拿着玻璃管由静止沿水平方向向右做匀加速直线运动,则该过程中关于红蜡块运动情况的描述正确的是( )
A. B.
C. D.
【答案】C
【解析】蜡烛参与水平向右的匀加速直线运动和竖直向上的匀速直线运动,合加速度的方向水平向右,合初速度方向与合加速度方向不在同一条直线上,必然做曲线运动,根据轨迹每点的切线方向表示速度的方向,轨迹的弯曲的方向大致与所受合力的方向一致,故 C正确,ABD错误。故选C。
2.竖直放置的封闭玻璃管内注满清水,内部有一个红蜡块。玻璃管倒置时蜡块以3m/s的速度向上匀速运动。在蜡块上升的同时,玻璃管以4m/s的速度水平向右运动,如图所示,此时蜡块实际运动的速度大小是( )
A.5m/s B.6m/s C.7m/s D.8m/s
【答案】A
【解析】竖直方向与水平方向的运动是蜡块的分运动,则蜡块的合速度为
故选A。
考点二:互成角度的两个匀速直线运动的合成
【例2】骑射项目是运动会上常见的一种娱乐项目,运动员骑在奔驰的马背上,弯弓射箭射击侧向的靶子目标M,其运动模型简化为如图所示的情境,假设运动员沿方向骑马的速度为,运动员静止时射出的弓箭速度为,直线跑道离固定目标M的最近距离为,假设运动员射箭位置与靶子等高,且垂直跑道方向射出弓箭。不计空气阻力和弓箭的重力,则运动员射出弓箭点的位置距离O点的距离x为( )
A. B. C. D.
【答案】B
【解析】弓箭沿方向和垂直于方向均做匀速直线运动,有
,
可知射出点在O点左侧,且到O点的距离为
故选B。
【变式练习】
1.小船过河时,垂直河岸方向的分速度为4m/s,沿河岸方向的分速度为3m/s,如图所示,小船过河的实际速度大小为( )
A.3m/s B.4m/s C.5m/s D.7m/s
【答案】C
【解析】根据平行四边形定则可知,小船过河的实际速度大小为
故选C。
2.春节期间人们放飞孔明灯表达对新年的祝福,如图所示,若孔明灯在竖直方向做匀速运动,在水平方向做匀速运动,孔明灯的运动轨迹可能为( )
A.直线 B.直线 C.曲线 D.曲线
【答案】B
【解析】孔明灯在竖直Oy方向做匀速运动,水平Ox方向做匀速运动,加速度为零,合力为零,因此孔明灯的运动轨迹可能为图中直线。故选B。
考点三:一个匀速和一个变速运动的合成
【例3】某研究性学习小组为了研究运动的合成与分解,利用图甲所示装置做了如下实验:在一端封闭、长约1m的均匀长直玻璃管内注满清水,水中放一个蜡块,将玻璃管的开口端用胶塞塞紧,然后将这个玻璃管倒置,蜡块能在玻璃管中以的速度匀速上升。若在蜡块上升的同时水平向右移动玻璃管,用y轴表示蜡块竖直方向的位移,x轴表示蜡块随玻璃管通过的水平位移,时刻蜡块位于坐标原点,描出蜡块的运动轨迹如图乙所示。下列说法正确的是( )
A.玻璃管向右匀速平移
B.蜡块做匀变速运动
C.蜡块所受合外力的方向沿图线的切线方向
D.时蜡块的速度大小为20cm/s
【答案】B
【解析】A.蜡块在玻璃管中以的速度匀速上升,由题图乙可知,从t=0时刻起,每1s内玻璃管通过的水平位移依次是2.5cm、7.5cm、12.5cm、17.5cm,可知玻璃管水平向右匀加速平移,选项A错误;
B.蜡块沿水平方向的加速度大小恒定,由运动学公式可知,水平方向的加速度大小为
所以蜡块做匀变速运动,选项B正确;C.做曲线运动的物体所受合外力方向指向轨迹内侧,选项C错误;D.由以上分析和速度的合成可知,t=2s时蜡块的速度大小为
选项D错误。故选B。
【变式练习】
1.方老师用装有水的玻璃管做“观察蜡块的运动”实验时,用气泡代替了蜡块,将玻璃管迅速倒置后,气泡沿着玻璃管加速上升,同时将玻璃管紧贴着黑板沿水平方向向右匀速移动,则气泡的实际运动轨迹可能为( )
A. B.
C. D.
【答案】B
【解析】A.由气泡加速上升,沿水平方向向右匀速移动可知气泡所受合力方向竖直向上,其合速度方向斜右上方,作图如下
故B正确,ACD错误。故选B。
2.在一次杂技表演中,表演者顶着杆沿水平地面运动,其x-t图像如图甲所示。与此同时猴子沿竖直杆向上运动,如图乙所示,其v-t图像如图丙所示,若以地面为参考系,下列说法中正确的是( )
A.猴子的运动轨迹为直线 B.t=1s时猴子的加速度大小为
C.第1s内和第2s内猴子的速度变化量不同 D.t=2s时猴子离出发点的距离为16m
【答案】B
【解析】A.由题意可知猴子在水平方向做匀速直线运动,在竖直方向做匀减速直线运动,其合运动为曲线运动,运动轨迹应为开口向下的抛物线的半支,故A错误;B.t=1s时猴子的加速度大小为
故B正确;C.猴子做匀变速曲线运动,第1s内和第2s内猴子的速度变化量相同,故C错误;D.t=2s时,猴子在水平和竖直方向的位移大小分别为
此时猴子离出发点的距离为
故D错误。故选B。
考点四:两个变速直线运动的合成
【例4】为了抗击病毒疫情,保障百姓基本生活,许多快递公司推出了“无接触配送”。快递小哥想到了用无人机配送快递的方法。某次配送快递无人机在飞行过程中,水平方向速度及竖直方向与飞行时间t的关系图像如图甲、图乙所示。关于无人机运动说法正确的是( )
A.时间内,无人机做曲线运动
B.t2时刻,无人机运动到最高点
C. 时间内,无人机做匀变速直线运动
D. 时刻,无人机的速度为
【答案】D
【解析】A.0~t1时间内,无人机在水平方向做初速度为零的匀加速运动,在竖直方向也做初速度为零的匀加速运动,则合运动为匀加速直线运动,选项A错误;B.时间内,无人机速度一直为正,即一直向上运动,则时刻,无人机还没有运动到最高点,选项B错误;C.时间内,无人机水平方向做速度为的匀速运动,竖直方向做匀减速运动,则合运动为匀变速曲线运动,选项C错误;D.t2时刻,无人机的水平速度为,竖直速度为,则合速度为,选项D正确。故选D。
【变式练习】
1.某质点在平面上运动,其在x轴方向和y轴方向上的图像分别如图甲和图乙所示。则下列判断正确的是( )
A.该质点的初速度为 B.前内质点的位移为
C.该质点做匀变速曲线运动 D.该质点有恒定的加速度,大小为
【答案】D
【解析】根据图像中图线的斜率表示加速度,由图甲可知,质点在在x轴方向上,初速度为
加速度为
由图乙可知,质点在在y轴方向上,初速度为
加速度为
A.根据运动的合成可知,该质点的初速度为
故A错误;CD.根据运动的合成可知,该质点的加速度为
即该质点有恒定的加速度,大小为,设加速度与轴的夹角为,初速度与轴的夹角为,根据几何关系可得
,
即质点的初速度与加速度方向相同,则质点做匀加速直线运动,故C错误D正确;
B.由于质点做匀加速直线运动,由运动学公式可得,前内质点的位移为
故B错误。故选D。
2.为保障灾民生命财产安全,消防队员利用无人机为灾民配送物资,某次在执行任务时,无人机从地面起飞,将配送物资运输到预定地点,在飞行过程中,通过速度传感器测出无人机水平方向和竖直方向的分速度vx和随飞行时间t的关系图像如图甲、乙所示,无人机到达最大高度后释放物资,物资落在预定地点,不计空气阻力,g取10m/s2,以下说法正确的是( )
A.在0~10s内,无人机做曲线运动
B.30s时无人机速度为10m/s
C.25s时无人机加速度大小为0.3m/s2
D.20s时物资从无人机上释放
【答案】B
【解析】A.0~10s时间内,无人机在水平方向上做初速度为零的匀加速运动,在竖直方向上做初速度为零的匀加速运动,则合运动为初速为零的匀加速直线运动,故A错误;
B.30s时刻无人机水平方向速度,竖直方向上速度,此时速度
故B正确;C.25s时无人机水平方向加速度为零,竖直方向加速度即为无人机的加速度,其大小为
故C错误;D.0~40s时间内无人机竖直方向上速度均向上,一直升高,无人机到达最大高度后释放物资,故40s时物资从无人机上释放,故D错误。故选B。
考点五:小船过河问题
【例5】如图所示,河宽L=200m,河水的流速大小为3m/s。一小船在静水中的速度4m/s,小船自A处出发,渡河时,船头始终垂直河岸方向,到达对岸B处。下列说法正确的是( )
A.小船渡河时间为40s
B.B点在A点下游120m
C.A、B两点间距离为250m
D.无论船头朝向何处,小船都不可以到达A点正对岸
【答案】C
【解析】A.渡河时,船头始终垂直河岸方向,则小船渡河时间
故A错误;B.船随水漂流
x=vst=3×50m=150m
即B点在A点下游150m,故B错误;C.根据平行四边形定则可知,A、B两点间距离
故C正确;D.分析可知,小船在静水中的速度大于河水的流速,当合速度与河岸垂直,小船到达正对岸,设静水中速度的方向与河岸的夹角为θ
当θ满足上述条件时,小船可以到达A点正对岸,故D错误。故选C。
【变式练习】
1.如图所示,一条小船从码头A过河,小船在静水中的速度为v,船头指向始终与河岸垂直(沿AA'方向)。当水流速度为时,小船运动到河对岸的码头B靠岸,AB与河岸的夹角为。当水流速度为时,小船运动到河对岸的码头C靠岸,AC与河岸的夹角为。下列说法正确的是( )
A.小船沿AB、AC过河的时间相等
B.小船沿AC过河的时间更长
C.
D.当水流速度为时,要使小船到达码头,船头应指向河的上游且与河岸夹角为
【答案】A
【解析】AB.因船头始终垂直于河岸,可知船过河的时间为
即小船沿AB、AC过河的时间相等,选项A正确,B错误;C.由题意可知
解得
选项C错误;
D.当水流速度为时,要使小船到达码头,则合速度应该垂直河对岸,船头应指向河的上游且与河岸夹角为
则
选项D错误。故选A。
2.一艘小船在静水中的速度大小为4m/s,河宽100m,河水流速大小为5m/s。则小船( )
A.运动的最大速度是4m/s B.运动的最小速度是3m/s
C.渡河的最短时间是25s D.渡河的最小位移是100m
【答案】C
【解析】AB.当船行驶方向与水流速同向,小船速度最大,为
当船行驶方向与水流速反向,小船速度最小,为
故AB错误;C.当静水速与河岸垂直时,渡河时间最短
故C正确;D.因为静水速小于水流速,可知合速度的方向不可能垂直于河岸,则小船不能垂直到对岸,最小距离不会等于100m,要大于100m,故D错误。故选C。
一、运动的合成与分解
1.合运动与分运动
(1)如果物体同时参与了几个运动,那么物体实际发生的运动就是合运动,参与的几个运动就是分运动.
(2)物体实际运动的位移、速度、加速度是它的合位移、合速度、合加速度,而分运动的位移、速度、加速度就是它的分位移、分速度、分加速度.
2.合运动与分运动的四个特性
等时性 各分运动与合运动同时发生和结束,时间相同
等效性 各分运动的共同效果与合运动的效果相同
同体性 各分运动与合运动是同一物体的运动
独立性 各分运动之间互不相干,彼此独立,互不影响
3.运动的合成与分解
(1)运动的合成与分解是指位移、速度、加速度的合成与分解.其合成、分解遵循平行四边形定则.
(2)对速度v进行分解时,不能随意分解,应按物体的实际运动效果进行分解.
二、合运动的性质与运动轨迹
1.分析两个互成角度的直线运动的合运动的性质时,应先求出合运动的合初速度v和合加速度a,然后进行判断.
(1)是否为匀变速的判断:
加速度或合力
(2)曲、直判断:
加速度或合力与速度方向
2.两个互成角度的直线运动的合运动轨迹的判断:
轨迹在合初速度v0与合加速度a之间,且向加速度一侧弯曲.
一、单选题
1.如图,商场内某顾客站在自动扶梯上随扶梯一起上行,扶梯与水平面夹角为,速度为,将速度沿水平和竖直方向分解,则顾客在竖直方向的分速度为( )
A. B. C. D.
【答案】B
【解析】根据几何关系可知
解得
故选B。
2.如图所示,在一端封闭的光滑细玻璃管中注满清水,水中放一红蜡块R(R可视为质点)。将玻璃管的开口端用胶塞塞紧后竖直倒置且与y轴重合,R从坐标原点开始运动的轨迹如图所示,则红蜡块R在x轴、y轴方向的运动情况可能是( )
A.x轴方向匀速直线运动,y轴方向匀速直线运动
B.x轴方向匀速直线运动,y轴方向匀加速直线运动
C.x轴方向匀减速直线运动,y轴方向匀速直线运动
D.x轴方向匀加速直线运动,y轴方向匀速直线运动
【答案】D
【解析】AB.若x轴方向匀速直线运动,根据运动轨迹的形状,则y轴方向的加速度方向沿y轴负方向,即y轴方向减速直线运动。故AB错误;CD.若y轴方向匀速直线运动,根据运动轨迹的形状,则x轴方向的加速度方向沿x轴正方向,即x轴方向加速直线运动。故C错误;D正确。故选D。
3.如图所示,水平地面上固定一个与水平面夹角为θ的斜杆A,另一竖直直杆B以速度v水平向左做匀速直线运动,所有接触点均光滑。在B杆运动的过程中,两杆交点P的速度大小为( )
A. B. C.v cos θ D.v sin θ
【答案】A
【解析】两杆的交点P参与了两个分运动:与B杆一起以速度v水平向左的匀速直线运动和沿B杆竖直向上的运动,交点P的实际运动方向沿A杆斜向上,如图所示,则交点P的速度大小为
故A正确BCD错误。故选A。
4.小船以一定的速率垂直河岸向对岸划去,当水流匀速时,它渡河的时间、发生的位移与水速的关系是( )
A.水速小时,位移小,时间亦小 B.水速大时,位移大,时间亦大
C.水速大时,位移大,但时间不变 D.位移、时间大小与水速大小无关
【答案】C
【解析】小船以一定的速率使船头垂直河岸向对岸划去,即垂直于河岸方向上的速度不变,根据
知水流速变化时,渡河的时间不变,水流速增大,则
在沿河岸方向上的位移增大,则合位移增大。故选C。
5.如图所示,一玻璃管中注满清水,水中放一软木做成的小圆柱体,其直径略小于玻璃管的直径,轻重大小适宜,使它在水中能匀速上浮。将玻璃管的开口端用胶塞塞紧,如图甲,现将玻璃管倒置,如图乙,在小圆柱体上升的同时,使玻璃管水平向右匀加速移动,经过一段时间,玻璃管移至图丙中虚线所示位置,且小圆柱体恰好运动到玻璃管的顶端。在下面四个图中,能正确反映小圆柱体运动轨迹的是( )
A. B.
C. D.
【答案】C
【解析】小圆柱体竖直向上做匀速直线运动,水平向右做初速度为零的匀加速直线运动,则
联立解得
(其中,)
故选C。
6.如图所示,河水流速以及渡船在静水中的划行速度大小均恒定,渡船从平直河岸边的A处开始渡河,当船头方向垂直河岸时,渡船到达正对岸岸边B处下游的C处,A、C连线与水流方向的夹角为60°。若要使渡船从A处开始渡河,能够沿直线到达B处,则船头方向与水流反方向的夹角θ的正切值应为( )
A. B. C. D.
【答案】A
【解析】设船在静水中的速度为v1,水速为v2,则
当船垂直渡河时
得
故选A。
7.洪涝灾害常常给我们国家带来巨大的经济损失,如图所示某救援队利用摩托艇将人员进行转移。已知水的流速恒为,水流的方向平行于河岸,摩托艇的速度恒为,河宽为。该救援队由河岸的P点出发,将被困人员转移到河对岸,连线与河岸垂直。则下列说法正确的是( )
A.如果,摩托艇可能到达Q
B.摩托艇运动到河对岸时的速度一定大于
C.摩托艇渡河的最短时间为
D.若摩托艇能到达Q,则渡河时间为
【答案】C
【解析】A.如果,摩托艇的合速度方向不可能垂直于河岸,所以摩托艇不可能到达Q,故A错误;B.若满足,则摩托艇的合速度方向可以垂直于河岸,当摩托艇以垂直河岸的合速度方向到达对岸时,摩托艇的合速度大小为
故B错误;C.当摩托艇分速度垂直于河岸时,渡河时间最短,则有
故C正确;D.若摩托艇能到达Q,则摩托艇的合速度方向垂直于河岸,此时合速度大小为
渡河时间为
故D错误。故选C。
8.如图所示,一艘走私船在岸边A点,以速度v0匀速地沿垂直于岸的方向逃跑,距离A点为处的B点的快艇同时启动追击,快艇的速率u大小恒定,方向总是指向走私船,恰好在距岸边的距离为a处逮住走私船,那么以下关于快艇速率的结论正确的是( )
A.快艇在垂直岸边的方向上的平均速度uy=v0
B.快艇在沿岸的方向上的平均速度ux=v0
C.快艇平均速度的大小
D.快艇的平均速率等于
【答案】A
【解析】A.从开始到追及的过程中,由于在垂直岸边的方向上,两船和快艇的位移及经历的时间相同,所以快艇在垂直于岸边的方向上的平均速度等于走私船的速度,即
uy=v0
故A正确;B.由快艇在沿河岸方向上的位移
与垂直于河岸方向上的位移
a=uyt
可知,快艇在沿岸边的方向上的平均速度为
故B错误;C.快艇发生的位移
再结合l=ut可得快艇的平均速度大小为
故C错误;
D.由于快艇运动中速度方向不停地变化,即快艇做曲线运动,则快艇通过的路程一定大于其位移 ,故平均速率一定大于 ,故D错误。故选A。
二、多选题
9.如图所示,甲、乙两船在同一条河流中同时开始渡河,河宽,、分别是甲、乙两船的出发点,两船头与河岸均成角,甲船船头恰好对准点的正对岸点,经过一段时间乙船恰好到达点,如果划船速度均为,且两船相遇不影响各自的航行。下列判断正确的是( )
A.水流方向向左,大小为
B.两船同时到达河对岸,花费时间均为
C.甲船水平位移为
D.甲乙两船会在上某点相遇
【答案】BD
【解析】A.以乙船为研究对象,如果水流方向向左,则如图1所示
则船的合速度方向为左斜向上,不可能会到达P点,则说明水流方向一定向右,且依题意乙船的合速度垂直对岸,则船向左的分速度与水流速度相抵消,可得
故A错误;B.两船在与垂直水流方向上的速度均为,且河宽均为d,则两船同时到达河对岸,根据运动的独立性,可知花费时间均为
故B正确;C.以甲船为研究对象,水流方向向右,则如图2所示
则船在水平方向上的速度为
则甲船水平位移为
故C错误;D.甲乙两船在纵向上的速度均为,且这也是乙的合速度,而甲船还有横向速度,相当于两船在纵向上相对静止,而横向上甲船以的水平速度靠近乙船,所以甲乙两船会在PN上某点相遇,故D正确。故选BD。
10.有关运动的合成,以下说法正确的是( )
A.两个直线运动的合运动一定是直线运动
B.两个不在一条直线上的匀速直线运动的合运动一定是直线运动
C.两个初速度为零的匀加速(加速度大小不相等)直线运动的合运动一定是匀加速直线运动
D.匀加速运动和匀速直线运动的合运动一定是直线运动
【答案】BC
【解析】B.选项中对两个直线运动的速度没有要求,可设初速度分别为、,如图所示
若两分运动为不在同一直线上的匀速直线运动,则根据平行四边形定则可得恒定,即做匀速直线运动,B正确;AD.若两分运动有加速度,还需把加速度合成,其加速度若与同向则加速,若与反向则减速,若与不在同一直线上则做曲线运动,AD错误;C.若两分运动的初速度均为零,则合运动为匀加速直线运动,C正确。故选BC。
11.先后将小球1、2由同一位置以不同的速度竖直向上抛出,抛出后小球只受重力和水平方向的风力作用,两小球的运动轨迹如图虚线所示,则两小球相比,下列说法正确的是( )
A.小球1的竖直向上抛出的初速度比2大
B.小球1从抛出到落地的运动时间比2短
C.小球2的水平方向上的平均速度一定比小球1的大
D.小球2所受的风力一定比小球1受到的大
【答案】AC
【解析】AB.小球的运动可以分解为竖直方向的竖直上抛和水平方向的匀加速直线运动,上升阶段竖直方向满足
依题意,可知小球1上升高度大于小球2的上升高度,所以小球1竖直向上抛出的初速度大,小球1从抛出到落地的运动时间长,故A正确,B错误;C.由图可知,小球1水平位移小,飞行时间长,根据水平方向的平均速度
分析知小球2的水平方向的平均速度一定比小球1的大,故C正确;D.小球水平方向满足
由图可知,小球1的飞行时间长,水平位移小,小球1的加速度小,但不知道两小球质量的关系,故不能判断出二者水平方向受力的关系,故D错误。故选AC。
三、实验题
12.冬奥会赛场利用了“高速运动目标跟踪拍摄系统”,不仅让观众看清了动作,还实现了对物体运动情况的多角度定量分析。
为观测冰球在不同方向上的运动情况,冰球场中用三台摄像机进行跟随拍摄,以记录冰球运动的时间、位置等信息。如图所示,在冰面上建立平面直角坐标系,其中设备A视角是竖直向下的,跟随冰球俯拍:设备B、C视角是水平的,分别沿x、y轴跟随拍摄,可以拍摄小球沿x轴、y轴的运动情况。
(1)对设备B拍摄的信息进行分析,得到以下数据,请在答题卡对应方格纸中作出冰球位置随时间变化的图像:
时刻 0 0.4 0.8 1.2 1.6 2.0
位置 0 8.0 16.0 23.8 32.1 39.8
(2)由设备B得到冰球速度大小是____________;
(3)同时,设备C得到冰球的速度大小为,设备A得到冰球的速度大小为。由此可以得出、、之间的数学关系式是____________;
(4)在某次比赛中,B、C设备测出的冰球的速度大小分别是和,则冰球实际运动速度的大小是______________,方向是____________(用实际速度与x轴的夹角的正切值表示)。
【答案】(2)19.9 (3) (4)17
【解析】(2)[1] 由设备B得到冰球速度大小是
(3)[2] 同时,设备C得到冰球的速度大小为,设备A得到冰球的速度大小为。由此可以得出、、之间的数学关系式是
(4)[3] 在某次比赛中,B、C设备测出的冰球的速度大小分别是和,则冰球实际运动速度的大小是
[4] 设实际速度与x轴的夹角为,则
四、解答题
13.小船要横渡一条d=200m宽的河,水流速度为v水=4m/s,船在静水中的航速是v船=5m/s,求:
(1)要使小船渡河时间最短,渡河时间是多少?位移大小是多少?
(2)要使小船渡河位移最短,船头应指向何处?多长时间能到达对岸?
【答案】(1)40s,;(2)船头与上游河岸的夹角为,
【解析】(1)要使小船渡河时间最短,船头要垂直河岸,如图1所示
渡河时间为
合速度为
位移大小为
(2)由于船速大于水速,当合速度垂直于河岸时,位移最短,如图2所示
设船头与上游河岸的夹角为,则
则
所以要使小船渡河位移最短,船头与上游河岸的夹角为。
合速度大小为
到达对岸时间为
