6.1.1向量的实际背景与概念课时练习-2022-2023学年高一下学期数学人教A版(2019)必修第二册(含答案)
文档属性
| 名称 | 6.1.1向量的实际背景与概念课时练习-2022-2023学年高一下学期数学人教A版(2019)必修第二册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 433.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-10 09:09:52 | ||
图片预览



文档简介
2022-2023学年度高一数学人教A版(2019)课时练习
6.1.1向量的实际背景与概念
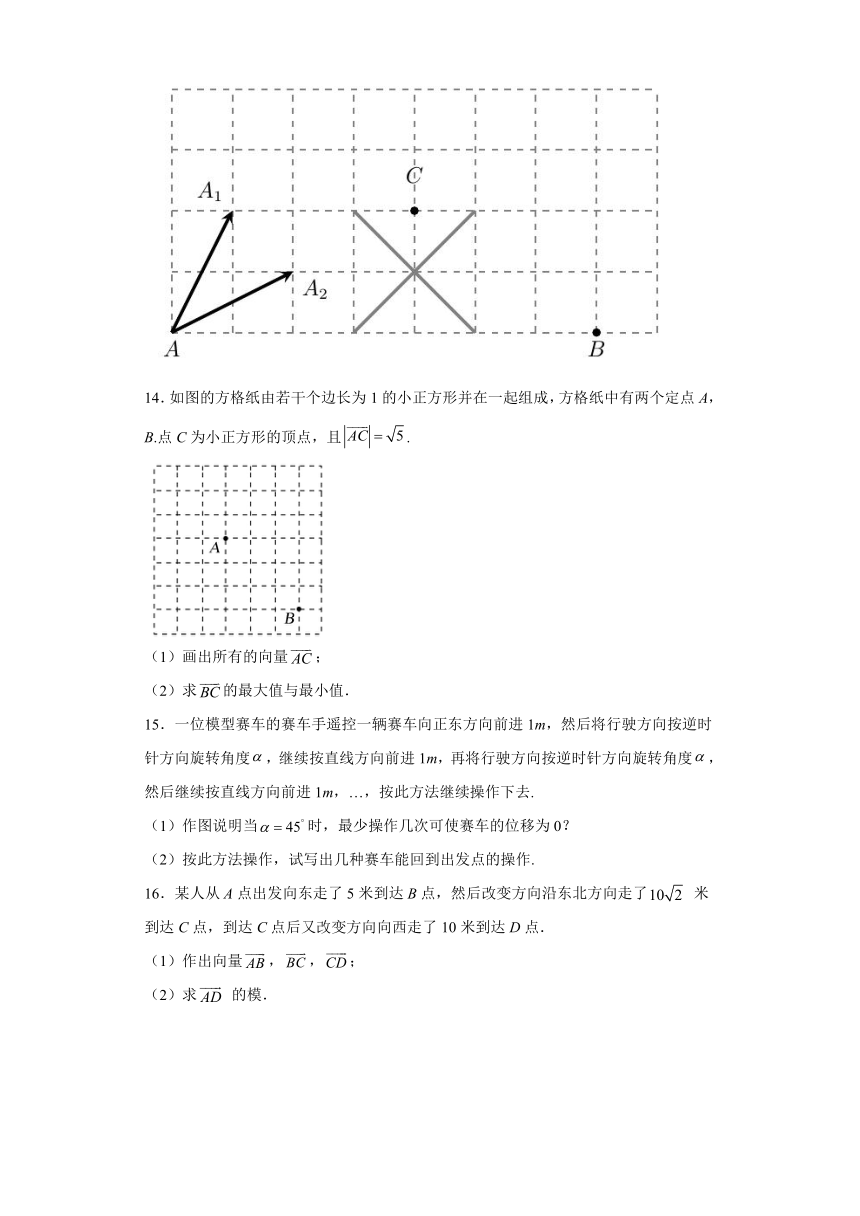
一、单选题
1.下列说法错误的是( )
A.向量与向量长度相等 B.单位向量都相等
C.向量的模可以比较大小 D.任一非零向量都可以平行移动
2.下列命题中正确的是
A.若,则 B.若,则
C.若,则与可能共线 D.若,则一定不与共线
3.在等式①; ②;③;④;⑤若,则;正确的个数是( )
A.0个 B.1个 C.2个 D.3个
4.下列命题中,正确的个数是( )
①单位向量都相等;
②模相等的两个平行向量是相等向量;
③若,满足且与同向,则;
④若两个向量相等,则它们的起点和终点分别重合;
⑤若∥∥,则∥.
A.0个 B.1个
C.2个 D.3个
5.下列四个命题正确的是( )
A.两个单位向量一定相等 B.若与不共线,则与都是非零向量
C.共线的单位向量必相等 D.两个相等的向量起点、方向、长度必须都相同
6.给出下列说法:①零向量是没有方向的;②零向量的长度为0;③零向量的方向是任意的;④单位向量的模都相等,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、多选题
7.下列说法中错误的是
A.向量与是共线向量,则A,B,C,D四点必在一条直线上
B.零向量与零向量共线
C.若,则
D.温度含零上温度和零下温度,所以温度是向量
8.下面的命题正确的有( )
A.方向相反的两个非零向量一定共线
B.单位向量都相等
C.若,满足且与同向,则
D.“若A、B、C、D是不共线的四点,且”“四边形ABCD是平行四边形”
三、填空题
9.向量=____.
10.如图,在长方体中,,,,以长方体的八个顶点中两点为起点和终点的向量中.
(1)单位向量共有______个;
(2)模为的向量有______;
(3)与相等的向量有______;
11.已知是两个非零向量,且,,则的最大值为_____.
12.若,,则______.
四、解答题
13.图是中国象棋的半个棋盘示意图,“马走日”是象棋中“马”的走法,“马”可从A跳到,也可从A跳到,用向量,表示“马”走了“一步”,试在图中画出“马”分别在B,C处走了“一步”的所有情况.
14.如图的方格纸由若干个边长为1的小正方形并在一起组成,方格纸中有两个定点A,B.点C为小正方形的顶点,且.
(1)画出所有的向量;
(2)求的最大值与最小值.
15.一位模型赛车的赛车手遥控一辆赛车向正东方向前进1m,然后将行驶方向按逆时针方向旋转角度,继续按直线方向前进1m,再将行驶方向按逆时针方向旋转角度,然后继续按直线方向前进1m,…,按此方法继续操作下去.
(1)作图说明当时,最少操作几次可使赛车的位移为0?
(2)按此方法操作,试写出几种赛车能回到出发点的操作.
16.某人从A点出发向东走了5米到达B点,然后改变方向沿东北方向走了 米到达C点,到达C点后又改变方向向西走了10米到达D点.
(1)作出向量,,;
(2)求 的模.
参考答案
1.B
【分析】A.由相反向量判断;B.由单位向量判断;C.由向量的长度是数量判断;D.由相等向量判断.
【详解】A.和长度相等,方向相反,故正确;
B.单位向量长度都为1,但方向不确定,故错误;
C.向量的长度可以比较大小,即模长可以比较大小,故正确;
D.向量只与长度和方向有关,与位置无关,故任一非零向量都可以平行移动,故正确.
故选:B.
2.C
【解析】利用共线向量、模的计算公式,即可得出.
【详解】因为向量既有大小又有方向,所以只有方向相同 大小(长度)相等的两个向量才相等,因此A错误;
两个向量不相等,但它们的模可以相等,故B错误;
无论两个向量的模是否相等,这两个向量都可能共线,故C正确,D错误.
故选:C
3.C
【解析】由零向量、向量数乘、点乘等概念和性质,即可判断正误,进而确定答案.
【详解】零向量与任何向量的数量积都为0,错误;
0乘以任何向量都为零向量,正确;
向量的加减、数乘满足结合律,而向量点乘不满足结合律,错误;
向量模的平方等于向量的平方,正确;
不一定有,故错误;
故选:C
4.A
【解析】根据平面向量的基本概念,对选项中的命题进行分析、判断正误即可.
【详解】解:对于①,单位向量的模长相等,但方向不一定相同,故①错误;
对于②,模相等的两个平行向量是相等向量或相反向量,故②错误;
对于③,向量是有方向的量,不能比较大小,故③错误;
对于④,向量是可以自由平移的矢量,
当两个向量相等时,它们的起点和终点不一定相同,故④错误;
对于⑤,时,若,则与不一定平行.
综上,以上正确的命题个数是0.
故选:A.
5.B
【解析】由相等向量、共线向量的概念逐一核对四个选项得答案.
【详解】解:两个单位向量一定相等错误,可能方向不同;
若与不共线,则与都是非零向量正确,原因是零向量与任意向量共线;
共线的单位向量必相等错误,可能是相反向量;
两个相等的向量的起点、方向、长度必须相同错误,原因是向量可以平移.
故选:B.
6.C
【分析】根据零向量及单位向量的概念即可求解.
【详解】解:对①:零向量的方向是任意的,故①错误;
对②:零向量的长度为0,故②正确;
对③:零向量的方向是任意的,故③正确;
对④:单位向量的模都等于1,故④正确.
故选:C.
7.AD
【解析】利用零向量,平行向量和共线向量的定义,判断各个选项是否正确,从而得出结论.
【详解】向量与是共线向量,则A,B,C,D四点不一定在一条直线上,故A错误;
零向量与任一向量共线,故B正确;
若,则,故C正确;
温度是数量,只有正负,没有方向,故D错误.
故选:AD
8.AD
【分析】根据向量的定义和性质,逐项判断正误即可.
【详解】对于A,由相反向量的概念可知A正确;
对于B,任意两个单位向量的模相等,其方向未必相同,故B错误;
对于C,向量之间不能比较大小,只能比较向量的模,故C错误;
对于D,若A、B、C、D是不共线的四点,且,
可得,且,故四边形ABCD是平行四边形;
若四边形ABCD是平行四边形,可知,且,
此时A、B、C、D是不共线的四点,且,故D正确.
故选:AD.
9.-
【分析】根据相等向量和相反向量的概念即可写出答案.
【详解】和是相反向量,故填-
故答案为:-
10. 、、、、、、、; 、、
【分析】根据单位向量、模、相等向量的概念结合图形进行分析求解.
【详解】(1)、由题意可知,,所以单位向量有、、、、、、、共个;
(2)、由图可知,在长方体中,,,所以左右两个侧面的对角线长度均为,即,所以模为的向量有:、、、、、、、;
(3)、由图可知,与相等的向量除它本身外有、、共个.
故答案为: ;、、、、、、、;、、
11.
【分析】构造,从而可知,于是的最大值可以利用基本不等式得到答案.
【详解】由题意,令,所以,,所以,所以,所以,当且仅当,且时取等号.故答案为.
12.或
【分析】根据和,确定模长和方向得到答案.
【详解】,故模相同,方向相同或相反
故或
故答案为:或
13.见解析
【解析】根据“马”走“日”得到答案.
【详解】解:如图所示.
(1)在B处“马”有3种走法,而在C处“马”有8种走法.
(2)用有向线段表示向量,一定要注意其方向,并用箭头在图中标出.
14.(1)见解析;(2)最大值为,最小值为.
【详解】试题分析:
(1)由||=及点C为小正方形的顶点和点A的位置可确定点C的位置,然后可画出.(2)根据(1)中的点C,逐一求得||后,可求得||的最大值为,最小值为.
试题解析:
(1)画出所有的向量,如图所示:
(2)由(1)所画的图知,
①当点C位于点C1或C2时,||取得最小值=;
②当点C位于点C5或C6时,||取得最大值=;
所以||的最大值为,最小值为.
15.(1)8次(2)答案不唯一,具体见解析
【解析】(1)位移为0表明赛车最后回到了出发点,作图时要弄清题意;
(2)讨论不同的的值求解即可.
【详解】
解:记出发点A.
(1)当时,如图①,赛车行进路线构成一个正八边形,最少操作8次可使赛车的位移为0,赛车所行路程是8m.
(2)当时,如图②,赛车行进路线构成一个正三角形,最少操作3次可使赛车回到出发点,赛车所行路程为3m;
当时,如图③,赛车行进路程构成一个正方形,最少操作4次可使赛车回到出发点,赛车所行路程为4m;
当时,如图④,赛车行进路线构成一个正六边形,最少操作6次可使赛车回到出发点,赛车所行路程为6m.
16.(1)见解析;(2)米
【解析】(1)利用方位根据向量的定义作出向量.
(2)根据(1)作出的平面图形,利用平面几何知识求解.
【详解】(1)作出向量,,;如图所示:
(2)由题意得,△BCD是直角三角形,其中∠BDC=90°,BC=10 米,CD=10米,
所以BD=10米.△ABD是直角三角形,其中∠ABD=90°,AB=5米,BD=10米,
所以AD==(米),
所以|米.
6.1.1向量的实际背景与概念
一、单选题
1.下列说法错误的是( )
A.向量与向量长度相等 B.单位向量都相等
C.向量的模可以比较大小 D.任一非零向量都可以平行移动
2.下列命题中正确的是
A.若,则 B.若,则
C.若,则与可能共线 D.若,则一定不与共线
3.在等式①; ②;③;④;⑤若,则;正确的个数是( )
A.0个 B.1个 C.2个 D.3个
4.下列命题中,正确的个数是( )
①单位向量都相等;
②模相等的两个平行向量是相等向量;
③若,满足且与同向,则;
④若两个向量相等,则它们的起点和终点分别重合;
⑤若∥∥,则∥.
A.0个 B.1个
C.2个 D.3个
5.下列四个命题正确的是( )
A.两个单位向量一定相等 B.若与不共线,则与都是非零向量
C.共线的单位向量必相等 D.两个相等的向量起点、方向、长度必须都相同
6.给出下列说法:①零向量是没有方向的;②零向量的长度为0;③零向量的方向是任意的;④单位向量的模都相等,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、多选题
7.下列说法中错误的是
A.向量与是共线向量,则A,B,C,D四点必在一条直线上
B.零向量与零向量共线
C.若,则
D.温度含零上温度和零下温度,所以温度是向量
8.下面的命题正确的有( )
A.方向相反的两个非零向量一定共线
B.单位向量都相等
C.若,满足且与同向,则
D.“若A、B、C、D是不共线的四点,且”“四边形ABCD是平行四边形”
三、填空题
9.向量=____.
10.如图,在长方体中,,,,以长方体的八个顶点中两点为起点和终点的向量中.
(1)单位向量共有______个;
(2)模为的向量有______;
(3)与相等的向量有______;
11.已知是两个非零向量,且,,则的最大值为_____.
12.若,,则______.
四、解答题
13.图是中国象棋的半个棋盘示意图,“马走日”是象棋中“马”的走法,“马”可从A跳到,也可从A跳到,用向量,表示“马”走了“一步”,试在图中画出“马”分别在B,C处走了“一步”的所有情况.
14.如图的方格纸由若干个边长为1的小正方形并在一起组成,方格纸中有两个定点A,B.点C为小正方形的顶点,且.
(1)画出所有的向量;
(2)求的最大值与最小值.
15.一位模型赛车的赛车手遥控一辆赛车向正东方向前进1m,然后将行驶方向按逆时针方向旋转角度,继续按直线方向前进1m,再将行驶方向按逆时针方向旋转角度,然后继续按直线方向前进1m,…,按此方法继续操作下去.
(1)作图说明当时,最少操作几次可使赛车的位移为0?
(2)按此方法操作,试写出几种赛车能回到出发点的操作.
16.某人从A点出发向东走了5米到达B点,然后改变方向沿东北方向走了 米到达C点,到达C点后又改变方向向西走了10米到达D点.
(1)作出向量,,;
(2)求 的模.
参考答案
1.B
【分析】A.由相反向量判断;B.由单位向量判断;C.由向量的长度是数量判断;D.由相等向量判断.
【详解】A.和长度相等,方向相反,故正确;
B.单位向量长度都为1,但方向不确定,故错误;
C.向量的长度可以比较大小,即模长可以比较大小,故正确;
D.向量只与长度和方向有关,与位置无关,故任一非零向量都可以平行移动,故正确.
故选:B.
2.C
【解析】利用共线向量、模的计算公式,即可得出.
【详解】因为向量既有大小又有方向,所以只有方向相同 大小(长度)相等的两个向量才相等,因此A错误;
两个向量不相等,但它们的模可以相等,故B错误;
无论两个向量的模是否相等,这两个向量都可能共线,故C正确,D错误.
故选:C
3.C
【解析】由零向量、向量数乘、点乘等概念和性质,即可判断正误,进而确定答案.
【详解】零向量与任何向量的数量积都为0,错误;
0乘以任何向量都为零向量,正确;
向量的加减、数乘满足结合律,而向量点乘不满足结合律,错误;
向量模的平方等于向量的平方,正确;
不一定有,故错误;
故选:C
4.A
【解析】根据平面向量的基本概念,对选项中的命题进行分析、判断正误即可.
【详解】解:对于①,单位向量的模长相等,但方向不一定相同,故①错误;
对于②,模相等的两个平行向量是相等向量或相反向量,故②错误;
对于③,向量是有方向的量,不能比较大小,故③错误;
对于④,向量是可以自由平移的矢量,
当两个向量相等时,它们的起点和终点不一定相同,故④错误;
对于⑤,时,若,则与不一定平行.
综上,以上正确的命题个数是0.
故选:A.
5.B
【解析】由相等向量、共线向量的概念逐一核对四个选项得答案.
【详解】解:两个单位向量一定相等错误,可能方向不同;
若与不共线,则与都是非零向量正确,原因是零向量与任意向量共线;
共线的单位向量必相等错误,可能是相反向量;
两个相等的向量的起点、方向、长度必须相同错误,原因是向量可以平移.
故选:B.
6.C
【分析】根据零向量及单位向量的概念即可求解.
【详解】解:对①:零向量的方向是任意的,故①错误;
对②:零向量的长度为0,故②正确;
对③:零向量的方向是任意的,故③正确;
对④:单位向量的模都等于1,故④正确.
故选:C.
7.AD
【解析】利用零向量,平行向量和共线向量的定义,判断各个选项是否正确,从而得出结论.
【详解】向量与是共线向量,则A,B,C,D四点不一定在一条直线上,故A错误;
零向量与任一向量共线,故B正确;
若,则,故C正确;
温度是数量,只有正负,没有方向,故D错误.
故选:AD
8.AD
【分析】根据向量的定义和性质,逐项判断正误即可.
【详解】对于A,由相反向量的概念可知A正确;
对于B,任意两个单位向量的模相等,其方向未必相同,故B错误;
对于C,向量之间不能比较大小,只能比较向量的模,故C错误;
对于D,若A、B、C、D是不共线的四点,且,
可得,且,故四边形ABCD是平行四边形;
若四边形ABCD是平行四边形,可知,且,
此时A、B、C、D是不共线的四点,且,故D正确.
故选:AD.
9.-
【分析】根据相等向量和相反向量的概念即可写出答案.
【详解】和是相反向量,故填-
故答案为:-
10. 、、、、、、、; 、、
【分析】根据单位向量、模、相等向量的概念结合图形进行分析求解.
【详解】(1)、由题意可知,,所以单位向量有、、、、、、、共个;
(2)、由图可知,在长方体中,,,所以左右两个侧面的对角线长度均为,即,所以模为的向量有:、、、、、、、;
(3)、由图可知,与相等的向量除它本身外有、、共个.
故答案为: ;、、、、、、、;、、
11.
【分析】构造,从而可知,于是的最大值可以利用基本不等式得到答案.
【详解】由题意,令,所以,,所以,所以,所以,当且仅当,且时取等号.故答案为.
12.或
【分析】根据和,确定模长和方向得到答案.
【详解】,故模相同,方向相同或相反
故或
故答案为:或
13.见解析
【解析】根据“马”走“日”得到答案.
【详解】解:如图所示.
(1)在B处“马”有3种走法,而在C处“马”有8种走法.
(2)用有向线段表示向量,一定要注意其方向,并用箭头在图中标出.
14.(1)见解析;(2)最大值为,最小值为.
【详解】试题分析:
(1)由||=及点C为小正方形的顶点和点A的位置可确定点C的位置,然后可画出.(2)根据(1)中的点C,逐一求得||后,可求得||的最大值为,最小值为.
试题解析:
(1)画出所有的向量,如图所示:
(2)由(1)所画的图知,
①当点C位于点C1或C2时,||取得最小值=;
②当点C位于点C5或C6时,||取得最大值=;
所以||的最大值为,最小值为.
15.(1)8次(2)答案不唯一,具体见解析
【解析】(1)位移为0表明赛车最后回到了出发点,作图时要弄清题意;
(2)讨论不同的的值求解即可.
【详解】
解:记出发点A.
(1)当时,如图①,赛车行进路线构成一个正八边形,最少操作8次可使赛车的位移为0,赛车所行路程是8m.
(2)当时,如图②,赛车行进路线构成一个正三角形,最少操作3次可使赛车回到出发点,赛车所行路程为3m;
当时,如图③,赛车行进路程构成一个正方形,最少操作4次可使赛车回到出发点,赛车所行路程为4m;
当时,如图④,赛车行进路线构成一个正六边形,最少操作6次可使赛车回到出发点,赛车所行路程为6m.
16.(1)见解析;(2)米
【解析】(1)利用方位根据向量的定义作出向量.
(2)根据(1)作出的平面图形,利用平面几何知识求解.
【详解】(1)作出向量,,;如图所示:
(2)由题意得,△BCD是直角三角形,其中∠BDC=90°,BC=10 米,CD=10米,
所以BD=10米.△ABD是直角三角形,其中∠ABD=90°,AB=5米,BD=10米,
所以AD==(米),
所以|米.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
