总复习面积问题专题(课件)人教版六年级上册数学(共19张PPT)
文档属性
| 名称 | 总复习面积问题专题(课件)人教版六年级上册数学(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 460.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 00:00:00 | ||
图片预览


文档简介
(共19张PPT)
面积问题
优翼
专题复习
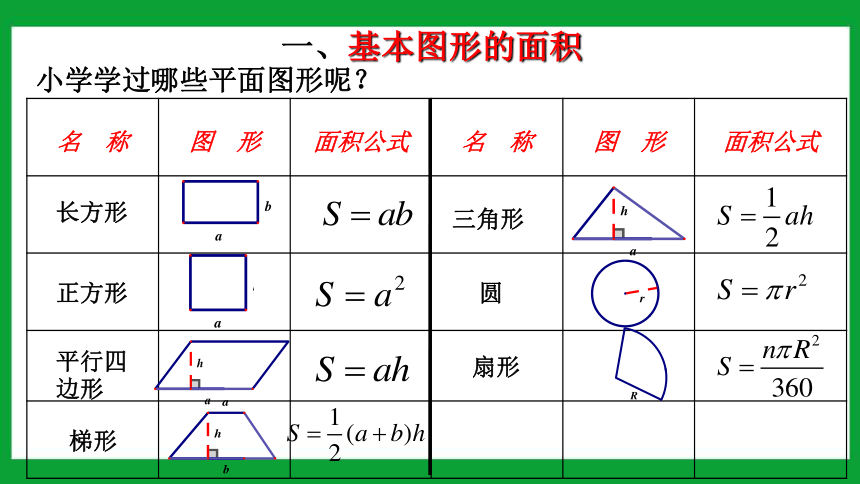
名 称 图 形 面积公式 名 称 图 形
面积公式
长方形
正方形
平行四边形
梯形
三角形
扇形
圆
一、基本图形的面积
小学学过哪些平面图形呢?
三角形的面积公式:
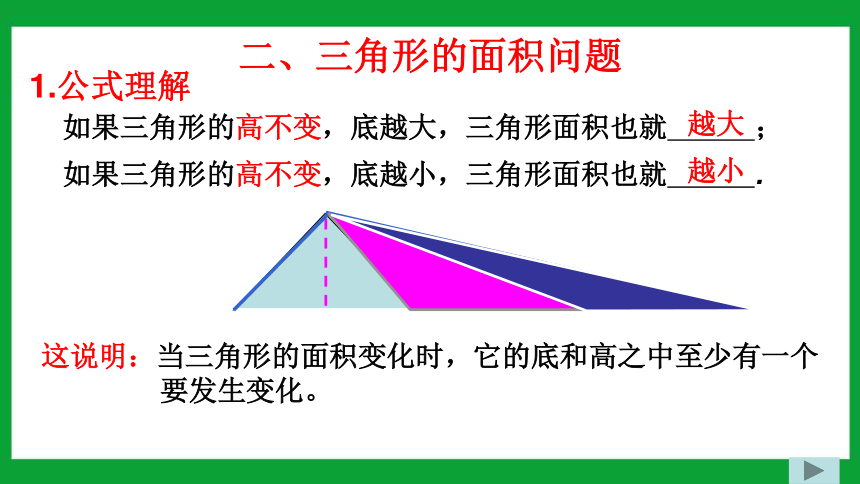
二、三角形的面积问题
基本图形:
如果三角形的底不变,高越大,三角形面积 ;
1.公式理解
如果三角形的底不变,高越小,三角形面积 .
越大
越小
如果三角形的高不变,底越大,三角形面积也就 ;
这说明:当三角形的面积变化时,它的底和高之中至少有一个
要发生变化。
如果三角形的高不变,底越小,三角形面积也就 .
二、三角形的面积问题
1.公式理解
越大
越小
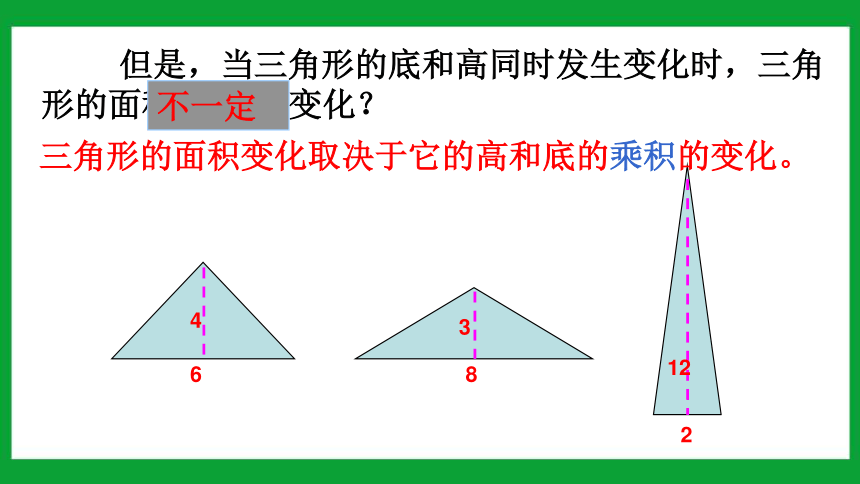
但是,当三角形的底和高同时发生变化时,三角形的面积 是否 变化?
6
4
3
8
2
12
不一定
三角形的面积变化取决于它的高和底的乘积的变化。
二、三角形的面积问题
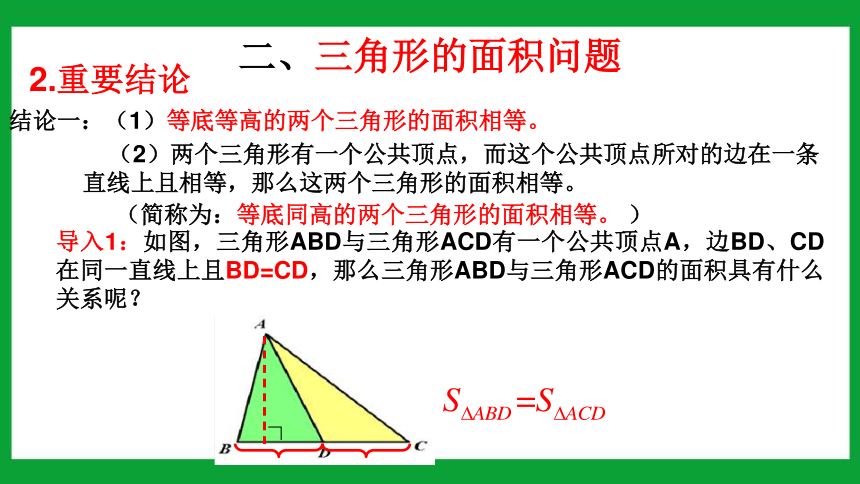
2.重要结论
结论一:(1)等底等高的两个三角形的面积相等。
(2)两个三角形有一个公共顶点,而这个公共顶点所对的边在一条直线上且相等,那么这两个三角形的面积相等。
∟
导入1:如图,三角形ABD与三角形ACD有一个公共顶点A,边BD、CD在同一直线上且BD=CD,那么三角形ABD与三角形ACD的面积具有什么关系呢?
(简称为:等底同高的两个三角形的面积相等。 )
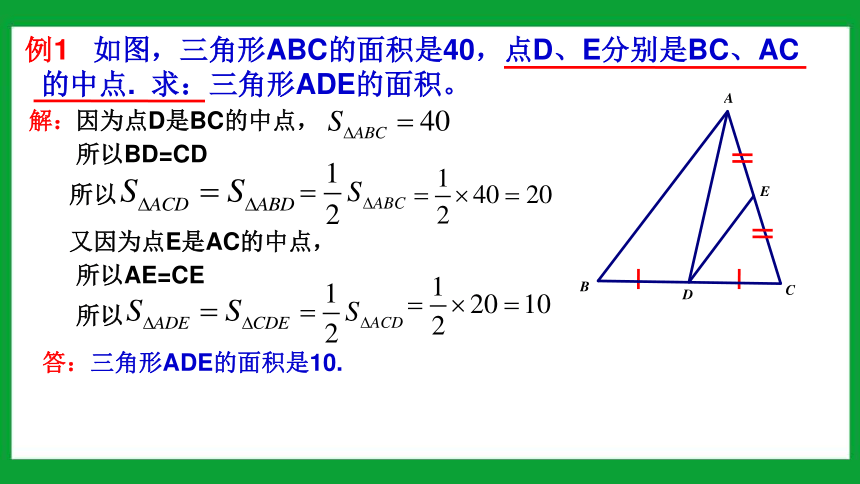
例1 如图,三角形ABC的面积是40,点D、E分别是BC、AC的中点. 求:三角形ADE的面积。
解:
因为点D是BC的中点,
所以BD=CD
所以
又因为点E是AC的中点,
所以AE=CE
所以
答:三角形ADE的面积是10.
变式 如图,三角形ABC的面积是40,点D、E和F分别是BC、AC和AD的中点. 求:三角形DEF的面积。
解:
因为点D是BC的中点,
所以BD=CD
所以
又因为点E是AC的中点,
所以AE=CE
所以
因为点F是AD的中点,
所以AF=DF
所以
答:三角形DEF的面积是5.
【方法总结】在运用等底等高、同底等高解决问题时,题干中通常会出现两边相等或某一点是某条线段的中点。
练习:如图,在三角形ABC中,D、E分别是AB、AC的中点,如果三角形AED的面积是30平方厘米.求三角形ABC的面积?
30
解:连接BE,
因为点D是AB的中点,
所以AD=BD
所以
所以
又因为点E是AC的中点,
所以AE=CE
所以
所以
答:三角形ABC的面积为120平方厘米。
∟
导入2:如图,三角形ABC、三角形ABD与三角形ABE有一条公共底边AB,点C、点D、点E在AB的平行线CE上,那么三角形ABC、三角形ABD与三角形ABE的面积具有什么关系呢?
结论二:两个三角形有一条公共的底边,而这条底边上的高相等,即这条底边所对的顶点在一条与底边平行的直线上,那么这两个三角形的面积相等。
二、三角形的面积问题
2.重要结论
(简称为:同底等高的两个三角形的面积相等。 )
例2 如图,梯形ABCD的高是8厘米,AC与BD是对角线,其交点O,BC=12厘米,三角形BOC的面积为32平方厘米。求三角形AOB和COD的面积.
解:在三角形ABC中, BC=12厘米,高是8厘米,
所以
因为
8
12
32
∟
所以
同理,在三角形DCB中, BC=12厘米,高是8厘米,
因为
所以
所以
答:三角形AOB和COD的面积都是16平方厘米.
变式 如图,在梯形ABCD中,AC与BD是对角线,其交点O,求证:三角形AOB与三角形COD面积相等.
解:因为在三角形ABC与三角形DCB中,底都是BC,高都是AD与BC平行线段的距离,
所以
所以
即证
【方法总结】:夹在一组平行线间的两个三角形若同底,则面积相同。
主要应用场景:正方形、长方形、平形四边行、梯形等。
练习: 如图,在边长为10厘米的正方形ABCD中,阴影部分的面积是40平方厘米,求四边形EFGH的面积。
答:四边形EFGH的面积为10平方厘米。
解:由题意得:
所以
导入3:在三角形ABC中,DC=2BD,三角形ABC的高为 ,那么三角形ABD与三角形ADC的面积具有什么关系呢?
解:由题意得:
因为 DC=2BD
所以
2份
1份
∟
二、三角形的面积问题
2.重要结论
导入4:在三角形ABC中,DC=3BD,三角形ABC的高为 ,那么三角形ABD与三角形ADC的面积具有什么关系呢?
3份
1份
∟
解:由题意得:
因为 DC=3BD
所以
结论三:(1)如果两个三角形等高,其中一个三角形的底是另一个三角形的底的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
(简称为:两个三角形高相等,面积之比等于底之比)
思考:将上面“导入”中条件“DC=3BD” 改为“DC=nBD”那么三角形ABD与三角形ADC的面积具有什么关系呢?
二、三角形的面积问题
2.重要结论
结论三:如果两个三角形等高(底),其中一个三角形的底(高)是另一个三角形的底(高)的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
(简称为:两个三角形高(底)相等,面积之比等于底(高)之比)
例3 如图,已知在三角形ABC中,BE=3AE,CD=2AD.若三角形ADE的面积为1平方厘米.求三角形ABC的面积。
1
解:连结BD,
因为 BE=3AE,
所以
3
所以
又因为 CD=2AD,
所以
所以
8
答:三角形ABC的面积为12平方厘米。
练习: 如图所示,在平行四边形ABCD中,E为AB的中点,AF=2CF,三角形AFE(图中阴影部分)的面积为8平方厘米。则平行四边形ABCD的面积是多少平方厘米?
解:连接FB,
又因为AF=2CF,
所以
因为E为AB的中点,
所以
所以
又因为
所以
答:平行四边形ABCD的面积是48平方厘米.
8
8
所以
所以
8
三、课堂小结
今天学习了哪些内容,你还有什么疑问吗?
四、课后作业
小题单作业41.
面积问题
优翼
专题复习
名 称 图 形 面积公式 名 称 图 形
面积公式
长方形
正方形
平行四边形
梯形
三角形
扇形
圆
一、基本图形的面积
小学学过哪些平面图形呢?
三角形的面积公式:
二、三角形的面积问题
基本图形:
如果三角形的底不变,高越大,三角形面积 ;
1.公式理解
如果三角形的底不变,高越小,三角形面积 .
越大
越小
如果三角形的高不变,底越大,三角形面积也就 ;
这说明:当三角形的面积变化时,它的底和高之中至少有一个
要发生变化。
如果三角形的高不变,底越小,三角形面积也就 .
二、三角形的面积问题
1.公式理解
越大
越小
但是,当三角形的底和高同时发生变化时,三角形的面积 是否 变化?
6
4
3
8
2
12
不一定
三角形的面积变化取决于它的高和底的乘积的变化。
二、三角形的面积问题
2.重要结论
结论一:(1)等底等高的两个三角形的面积相等。
(2)两个三角形有一个公共顶点,而这个公共顶点所对的边在一条直线上且相等,那么这两个三角形的面积相等。
∟
导入1:如图,三角形ABD与三角形ACD有一个公共顶点A,边BD、CD在同一直线上且BD=CD,那么三角形ABD与三角形ACD的面积具有什么关系呢?
(简称为:等底同高的两个三角形的面积相等。 )
例1 如图,三角形ABC的面积是40,点D、E分别是BC、AC的中点. 求:三角形ADE的面积。
解:
因为点D是BC的中点,
所以BD=CD
所以
又因为点E是AC的中点,
所以AE=CE
所以
答:三角形ADE的面积是10.
变式 如图,三角形ABC的面积是40,点D、E和F分别是BC、AC和AD的中点. 求:三角形DEF的面积。
解:
因为点D是BC的中点,
所以BD=CD
所以
又因为点E是AC的中点,
所以AE=CE
所以
因为点F是AD的中点,
所以AF=DF
所以
答:三角形DEF的面积是5.
【方法总结】在运用等底等高、同底等高解决问题时,题干中通常会出现两边相等或某一点是某条线段的中点。
练习:如图,在三角形ABC中,D、E分别是AB、AC的中点,如果三角形AED的面积是30平方厘米.求三角形ABC的面积?
30
解:连接BE,
因为点D是AB的中点,
所以AD=BD
所以
所以
又因为点E是AC的中点,
所以AE=CE
所以
所以
答:三角形ABC的面积为120平方厘米。
∟
导入2:如图,三角形ABC、三角形ABD与三角形ABE有一条公共底边AB,点C、点D、点E在AB的平行线CE上,那么三角形ABC、三角形ABD与三角形ABE的面积具有什么关系呢?
结论二:两个三角形有一条公共的底边,而这条底边上的高相等,即这条底边所对的顶点在一条与底边平行的直线上,那么这两个三角形的面积相等。
二、三角形的面积问题
2.重要结论
(简称为:同底等高的两个三角形的面积相等。 )
例2 如图,梯形ABCD的高是8厘米,AC与BD是对角线,其交点O,BC=12厘米,三角形BOC的面积为32平方厘米。求三角形AOB和COD的面积.
解:在三角形ABC中, BC=12厘米,高是8厘米,
所以
因为
8
12
32
∟
所以
同理,在三角形DCB中, BC=12厘米,高是8厘米,
因为
所以
所以
答:三角形AOB和COD的面积都是16平方厘米.
变式 如图,在梯形ABCD中,AC与BD是对角线,其交点O,求证:三角形AOB与三角形COD面积相等.
解:因为在三角形ABC与三角形DCB中,底都是BC,高都是AD与BC平行线段的距离,
所以
所以
即证
【方法总结】:夹在一组平行线间的两个三角形若同底,则面积相同。
主要应用场景:正方形、长方形、平形四边行、梯形等。
练习: 如图,在边长为10厘米的正方形ABCD中,阴影部分的面积是40平方厘米,求四边形EFGH的面积。
答:四边形EFGH的面积为10平方厘米。
解:由题意得:
所以
导入3:在三角形ABC中,DC=2BD,三角形ABC的高为 ,那么三角形ABD与三角形ADC的面积具有什么关系呢?
解:由题意得:
因为 DC=2BD
所以
2份
1份
∟
二、三角形的面积问题
2.重要结论
导入4:在三角形ABC中,DC=3BD,三角形ABC的高为 ,那么三角形ABD与三角形ADC的面积具有什么关系呢?
3份
1份
∟
解:由题意得:
因为 DC=3BD
所以
结论三:(1)如果两个三角形等高,其中一个三角形的底是另一个三角形的底的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
(简称为:两个三角形高相等,面积之比等于底之比)
思考:将上面“导入”中条件“DC=3BD” 改为“DC=nBD”那么三角形ABD与三角形ADC的面积具有什么关系呢?
二、三角形的面积问题
2.重要结论
结论三:如果两个三角形等高(底),其中一个三角形的底(高)是另一个三角形的底(高)的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
(简称为:两个三角形高(底)相等,面积之比等于底(高)之比)
例3 如图,已知在三角形ABC中,BE=3AE,CD=2AD.若三角形ADE的面积为1平方厘米.求三角形ABC的面积。
1
解:连结BD,
因为 BE=3AE,
所以
3
所以
又因为 CD=2AD,
所以
所以
8
答:三角形ABC的面积为12平方厘米。
练习: 如图所示,在平行四边形ABCD中,E为AB的中点,AF=2CF,三角形AFE(图中阴影部分)的面积为8平方厘米。则平行四边形ABCD的面积是多少平方厘米?
解:连接FB,
又因为AF=2CF,
所以
因为E为AB的中点,
所以
所以
又因为
所以
答:平行四边形ABCD的面积是48平方厘米.
8
8
所以
所以
8
三、课堂小结
今天学习了哪些内容,你还有什么疑问吗?
四、课后作业
小题单作业41.
