2022-2023学年高一下学期数学人教A版(2019)必修第二册6.2.4向量的数量积(二) 课件(15张PPT)
文档属性
| 名称 | 2022-2023学年高一下学期数学人教A版(2019)必修第二册6.2.4向量的数量积(二) 课件(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-10 00:00:00 | ||
图片预览





文档简介
6.2.4 向量的数量积
(二)
复习导入
向量a与b的数量积的含义是什么?向量的数量积具有哪些运算性质?
a·b=|a||b|cosθ,其中θ为向量a与b的夹角
设a,b是非零向量,它们的夹角是θ,e是与b方向相同的单位向量,则
(1) a·e= e·a =|a|cosθ.
(2)a⊥b? a·b=0.(直线垂直的条件)
(3)当a与b同向时,a·b=|a||b|;当a与b反向时,a·b=-|a||b|.特别地,a·a=|a|2或|a|= .(长度)
(4)|a·b|≤|a||b|.(由|cosθ|≤1得到)
(a向量在b向量上的投影向量)
新知探究
与向量的线性运算一样,定义了向量的数量积后,就要研究一下数量积运算是否满足一些运算律.
思考:类比数的乘法运算律,结合向量的线性运算的运算律,你能得到数量积运算的哪些运算律?
大胆猜想小心求证
新知探究
大胆猜想小心求证
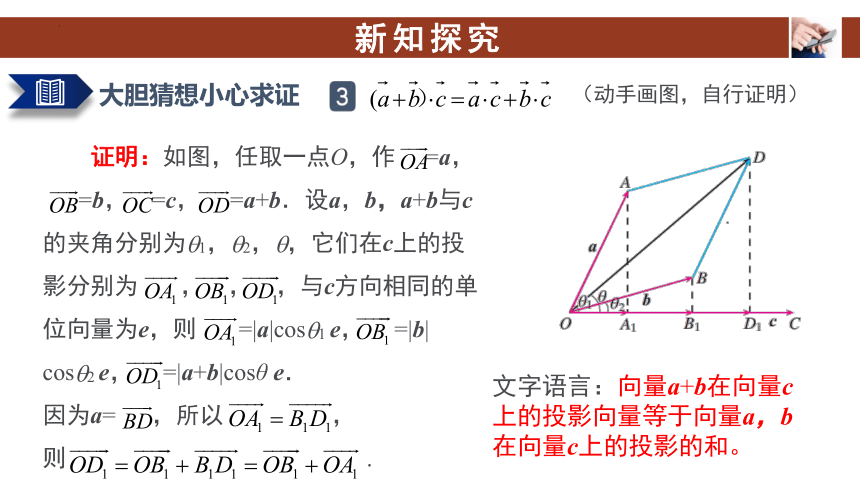
证明:如图,任取一点O,作 =a,
=b, =c, =a+b.设a,b,a+b与c的夹角分别为?1,?2,?,它们在c上的投影分别为 , , ,与c方向相同的单位向量为e,则 =|a|cos?1 e, =|b| cos?2 e, =|a+b|cosθ e.
因为a= ,所以 ,
则 .
文字语言:向量a+b在向量c上的投影向量等于向量a,b在向量c上的投影的和。
(动手画图,自行证明)
新知探究
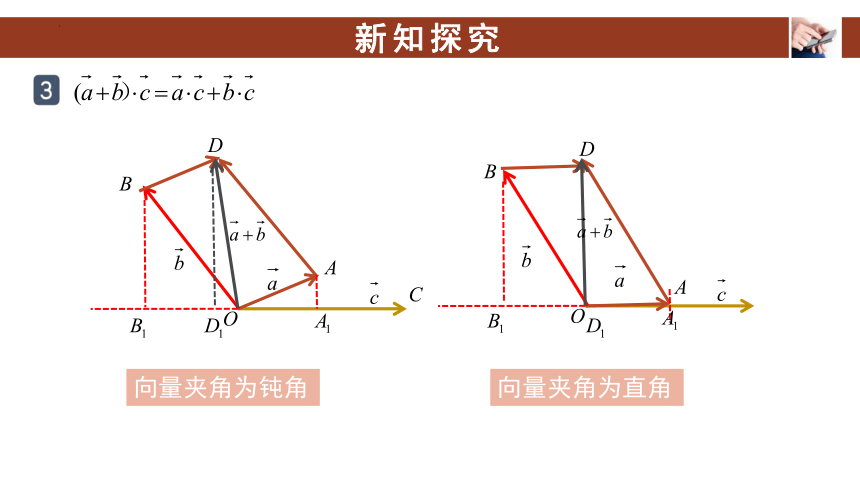
向量夹角为钝角
向量夹角为直角
新知探究
数量积运算律
(交换律)
(数乘结合律)
(分配律)
新知探究
问题
所得结果为一个与 共线的向量;
所得结果为一个与 共线的向量;
与 不一定共线,故结论不一定成立。
新知巩固
例1 我们知道,对任意a,b∈R,恒有
(a+b)2=a2+2ab+b2,(a+b)(a-b)=a2-b2.
对任意向量a,b,是否也有下面类似的结论?
(1)(a+b)2=a2+2a·b+b2;
(2)(a+b)·(a-b)=a2-b2.
(1)(a+b)2
=(a+b)·(a+b)
=a·a+a·b+b·a+b·b
=a2+2a·b+b2;
(2)(a+b)·(a-b)
=a·a-a·b+b·a-b·b
=a2-b2.
解:
新知巩固
例2 已知|a|=6,|b|=4,a与b的夹角为60?,求(a+2b)·(a-3b).
解:(a+2b)·(a-3b)
=a·a-3a·b+2b·a-6b·b
=|a|2-a·b-6|b|2
=|a|2-|a||b|cos?-6|b|2
=62-6×4×cos60?-6×42
=-72.
新知巩固
例3 已知|a|=3,|b|=4,且a与b不共线.当k为何值时,向量a+kb与a-kb互相垂直?
解:a+kb与a-kb互相垂直的充要条件是
(a+kb)·(a-kb)=0,
即a2-k2b2=0.
因为 a2=32=9,b2=42=16,所以 9-16k2=0.
因此 k= .
也就是说,当k= 时,a+kb与a-kb互相垂直.
课堂练习
1. 已知|????|=1, |????|=2, |????|=3, 向量????与????的夹角为???????? ,向量????与????的夹角为???????? , 计算:
?
(1) (????·????)???? ; (2) ????(????·????) .
?
2. 已知|????|=????, |????|=1, 且?????????与????+????????互相垂直, 求证????⊥????.
?
课堂练习
12
课堂练习
13
梳理总结
这一节课我们学习了哪些知识?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}运算律
实数乘法
向量数量积
交换律
????????=????????
?????????=?????????
分配律
(????+????)????=????????+????????
(????+????)?????=?????????+?????????
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}多项式乘法
向量数量积
(????+????)2=????2+2????????+????2
(????+????)????=????????+?????????????+????????
(?????????)2=????2?2????????+????2
(?????????)????=????????????????????+????????
(????+????)(?????????)=????2?????2
(????+????)(?????????)=?????????????????
平面向量数量积的运算律
平面向量数量积的运算性质
再 见
(二)
复习导入
向量a与b的数量积的含义是什么?向量的数量积具有哪些运算性质?
a·b=|a||b|cosθ,其中θ为向量a与b的夹角
设a,b是非零向量,它们的夹角是θ,e是与b方向相同的单位向量,则
(1) a·e= e·a =|a|cosθ.
(2)a⊥b? a·b=0.(直线垂直的条件)
(3)当a与b同向时,a·b=|a||b|;当a与b反向时,a·b=-|a||b|.特别地,a·a=|a|2或|a|= .(长度)
(4)|a·b|≤|a||b|.(由|cosθ|≤1得到)
(a向量在b向量上的投影向量)
新知探究
与向量的线性运算一样,定义了向量的数量积后,就要研究一下数量积运算是否满足一些运算律.
思考:类比数的乘法运算律,结合向量的线性运算的运算律,你能得到数量积运算的哪些运算律?
大胆猜想小心求证
新知探究
大胆猜想小心求证
证明:如图,任取一点O,作 =a,
=b, =c, =a+b.设a,b,a+b与c的夹角分别为?1,?2,?,它们在c上的投影分别为 , , ,与c方向相同的单位向量为e,则 =|a|cos?1 e, =|b| cos?2 e, =|a+b|cosθ e.
因为a= ,所以 ,
则 .
文字语言:向量a+b在向量c上的投影向量等于向量a,b在向量c上的投影的和。
(动手画图,自行证明)
新知探究
向量夹角为钝角
向量夹角为直角
新知探究
数量积运算律
(交换律)
(数乘结合律)
(分配律)
新知探究
问题
所得结果为一个与 共线的向量;
所得结果为一个与 共线的向量;
与 不一定共线,故结论不一定成立。
新知巩固
例1 我们知道,对任意a,b∈R,恒有
(a+b)2=a2+2ab+b2,(a+b)(a-b)=a2-b2.
对任意向量a,b,是否也有下面类似的结论?
(1)(a+b)2=a2+2a·b+b2;
(2)(a+b)·(a-b)=a2-b2.
(1)(a+b)2
=(a+b)·(a+b)
=a·a+a·b+b·a+b·b
=a2+2a·b+b2;
(2)(a+b)·(a-b)
=a·a-a·b+b·a-b·b
=a2-b2.
解:
新知巩固
例2 已知|a|=6,|b|=4,a与b的夹角为60?,求(a+2b)·(a-3b).
解:(a+2b)·(a-3b)
=a·a-3a·b+2b·a-6b·b
=|a|2-a·b-6|b|2
=|a|2-|a||b|cos?-6|b|2
=62-6×4×cos60?-6×42
=-72.
新知巩固
例3 已知|a|=3,|b|=4,且a与b不共线.当k为何值时,向量a+kb与a-kb互相垂直?
解:a+kb与a-kb互相垂直的充要条件是
(a+kb)·(a-kb)=0,
即a2-k2b2=0.
因为 a2=32=9,b2=42=16,所以 9-16k2=0.
因此 k= .
也就是说,当k= 时,a+kb与a-kb互相垂直.
课堂练习
1. 已知|????|=1, |????|=2, |????|=3, 向量????与????的夹角为???????? ,向量????与????的夹角为???????? , 计算:
?
(1) (????·????)???? ; (2) ????(????·????) .
?
2. 已知|????|=????, |????|=1, 且?????????与????+????????互相垂直, 求证????⊥????.
?
课堂练习
12
课堂练习
13
梳理总结
这一节课我们学习了哪些知识?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}运算律
实数乘法
向量数量积
交换律
????????=????????
?????????=?????????
分配律
(????+????)????=????????+????????
(????+????)?????=?????????+?????????
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}多项式乘法
向量数量积
(????+????)2=????2+2????????+????2
(????+????)????=????????+?????????????+????????
(?????????)2=????2?2????????+????2
(?????????)????=????????????????????+????????
(????+????)(?????????)=????2?????2
(????+????)(?????????)=?????????????????
平面向量数量积的运算律
平面向量数量积的运算性质
再 见
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
