人教A版(2019)高二数学选择性必修第二册课件 4.2.2等差数列的前n项和 第一课时(共30张PPT)
文档属性
| 名称 | 人教A版(2019)高二数学选择性必修第二册课件 4.2.2等差数列的前n项和 第一课时(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-10 21:27:46 | ||
图片预览






文档简介
(共30张PPT)
4.2.2
等差数列的前n项的和(1)
选择性必修第二册 第四章 数列
学习目标
1.了解等差数列的前n项和公式发现的背景;
2.推导并掌握等差数列的前n项和公式;
3.能在具体的问题情境中,能运用等差数列的前n项和公式解决一些简单的数学问题和实际问题;
4.核心素养:数学建模、数学推理、数学运算。
高斯(Gauss,1777-1855),德国著名数学家,他研究的内容涉及数学的各个领域,被称为历史上最伟大的三位数学家之一,他与阿基米德、牛顿齐名,是数学史上一颗光芒四射的巨星,被誉为“数学王子”.
一、情景引入
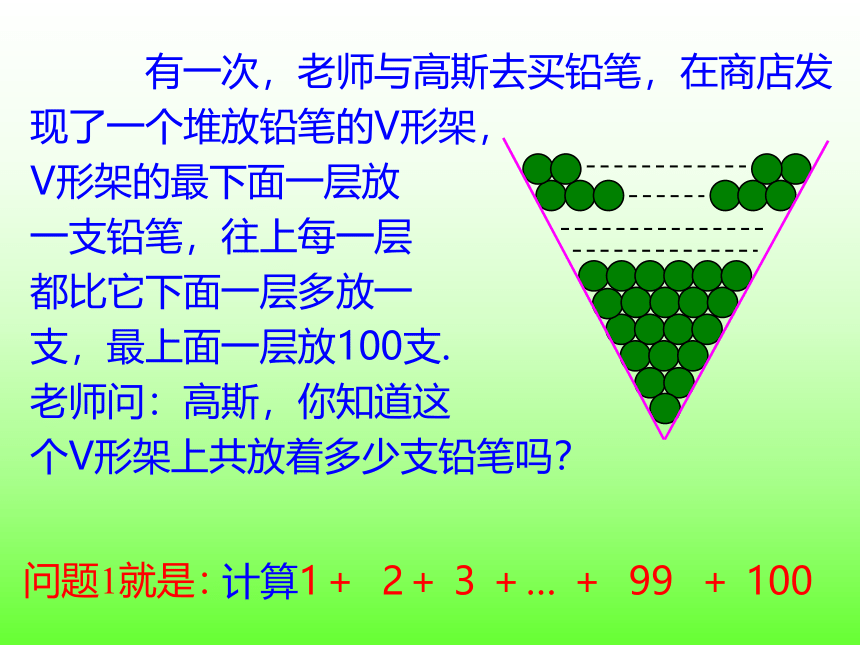
有一次,老师与高斯去买铅笔,在商店发
现了一个堆放铅笔的V形架,
V形架的最下面一层放
一支铅笔,往上每一层
都比它下面一层多放一
支,最上面一层放100支.
老师问:高斯,你知道这
个V形架上共放着多少支铅笔吗?
问题1就是:
计算1+ 2+ 3 +… + 99 + 100
高斯的算法
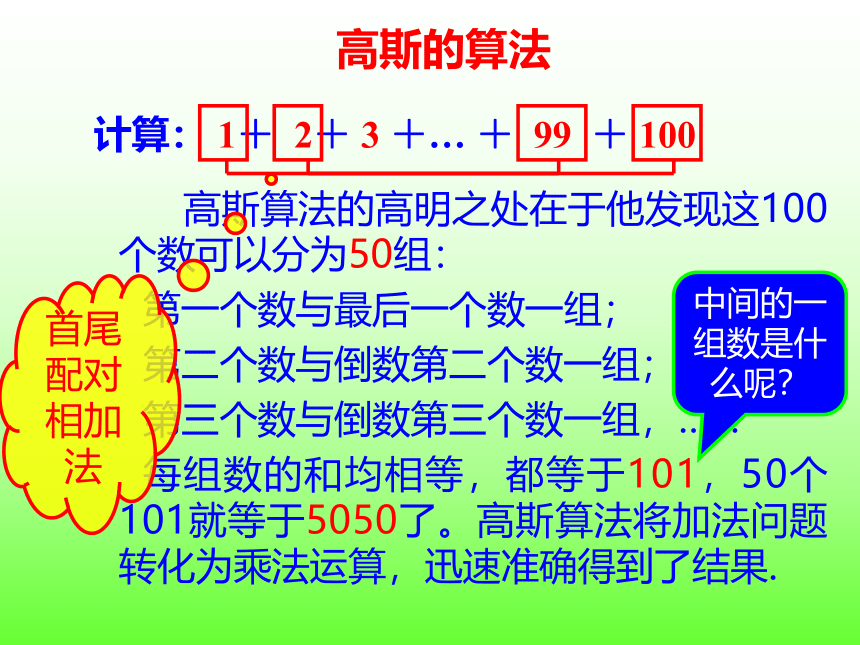
计算: 1+ 2+ 3 +… + 99 + 100
高斯算法的高明之处在于他发现这100个数可以分为50组:
第一个数与最后一个数一组;
第二个数与倒数第二个数一组;
第三个数与倒数第三个数一组,……
每组数的和均相等,都等于101,50个101就等于5050了。高斯算法将加法问题转化为乘法运算,迅速准确得到了结果.
首尾配对相加法
中间的一组数是什么呢?
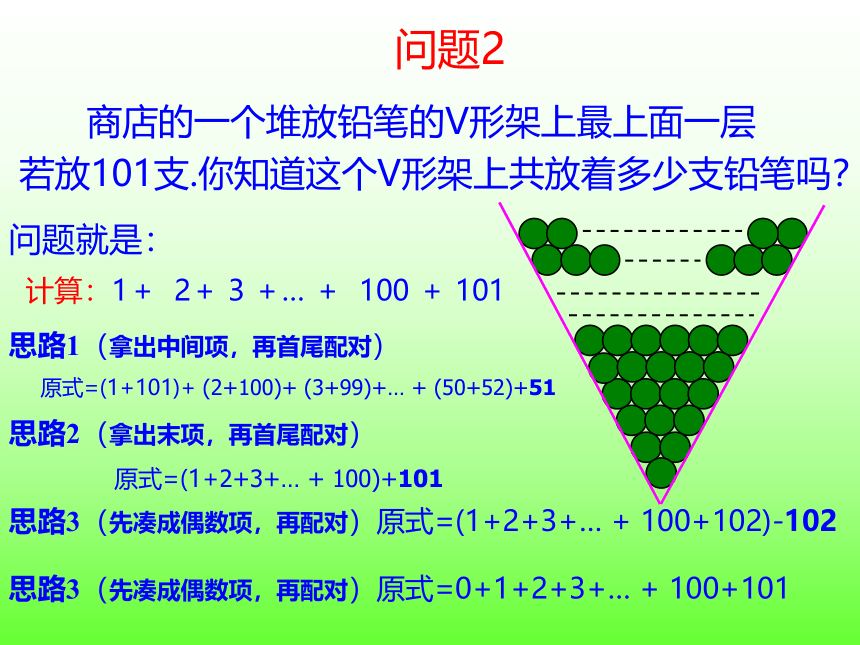
商店的一个堆放铅笔的V形架上最上面一层
若放101支.你知道这个V形架上共放着多少支铅笔吗?
问题2
问题就是:
计算:1+ 2+ 3 +… + 100 + 101
思路1(拿出中间项,再首尾配对)
原式=(1+101)+ (2+100)+ (3+99)+… + (50+52)+51
思路2(拿出末项,再首尾配对)
原式=(1+2+3+… + 100)+101
思路3(先凑成偶数项,再配对)原式=(1+2+3+… + 100+102)-102
思路3(先凑成偶数项,再配对)原式=0+1+2+3+… + 100+101
1.问题呈现
泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一。陵寝以宝石镶饰,图案之细致令人叫绝。
传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见左图),奢靡之程度,可见一斑。
你知道这个图案一共花了多少宝石吗?
二、探究新知
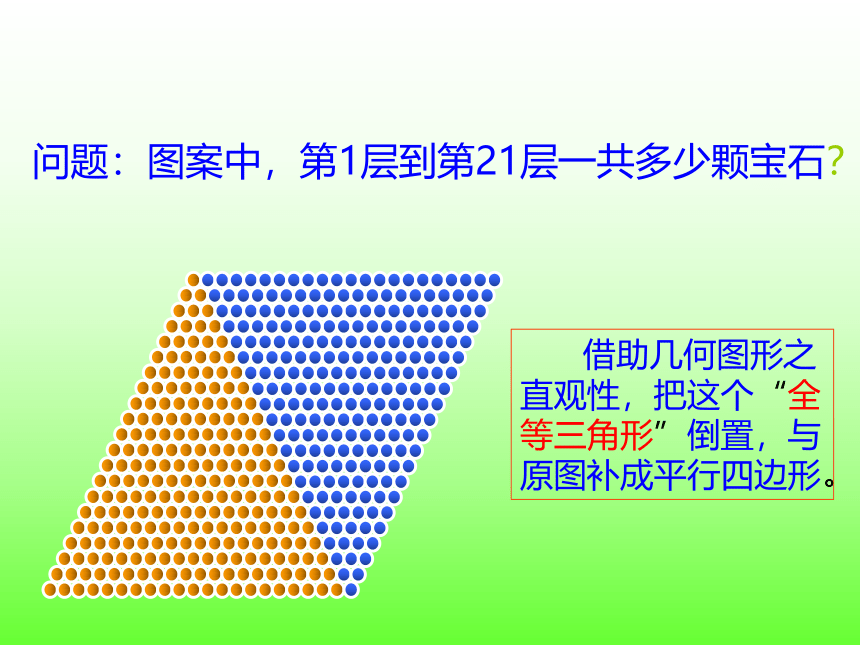
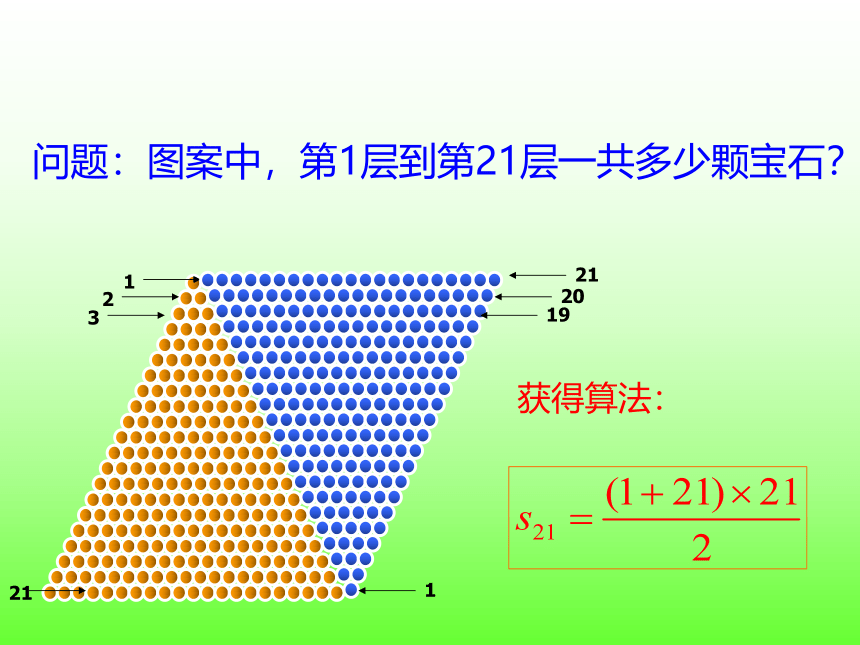
问题:图案中,第1层到第21层一共多少颗宝石?
这是求奇数个项和的问题,不能简单模仿偶数个项求和的办法,需要把中间项11看成首、尾两项1和21的等差中项。
通过前后比较得出认识:高斯“首尾配对” 的算法还得分奇、偶个项的情况求和。
有无简单的方法?
借助几何图形之直观性,把这个“全等三角形”倒置,与原图补成平行四边形。
问题:图案中,第1层到第21层一共多少颗宝石?
1
2
3
21
21
20
19
1
获得算法:
问题:图案中,第1层到第21层一共多少颗宝石?
探究了以上两个实际问题的求和,我们对数列求和有了一定的认识,那么能否将“倒序相加法”推广到任意一个等差数列呢?
这种方法不需分奇、偶个项的情况就可以求和, 很有创意,用数学式子表示就是:
1+ 2+ 3+ 4+……+21
21+20+19+18+……+1
对齐相加(其中下第二行的式子与第一行的
式子恰好是倒序)
这实质上是我们数学中一种求和的重要方法
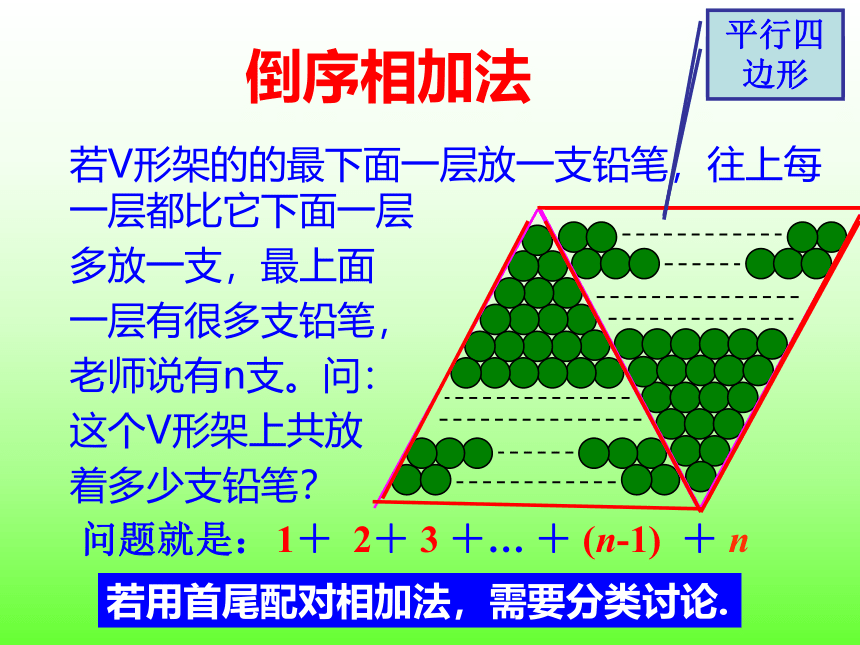
倒序相加法
若V形架的的最下面一层放一支铅笔,往上每一层都比它下面一层
多放一支,最上面
一层有很多支铅笔,
老师说有n支。问:
这个V形架上共放
着多少支铅笔?
问题就是:
1+ 2+ 3 +… + (n-1) + n
若用首尾配对相加法,需要分类讨论.
三角形
平行四边形
倒序相加法
n + (n-1) + (n-2) +…+ 2 +1
那么,对一般的等差数列,如何求它的
前n项和呢?
分析:这其实是求一个具体的等差数列前n项和.
①
②
倒序相加法
已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .
如何才能将等式的右边化简?
①
②
倒序相加法
2.等差数列求和公式
等差数列的前n项和的公式:
思考:(1)公式的文字语言;
(2)公式的特点;
不含d
可知三求一
等差数列的前n项和等于首末两项的和与项数乘积的一半。
公式的记忆
我们可结合梯形的面积公式来记忆
等差数列前 n 项和公式.
n
a1
an
公式的记忆
a1
(n-1)d
n
a1
an
将图形分割成一个平行四边形和一个三角形.
我们可结合梯形的面积公式来记忆
等差数列前 n 项和公式.
在等差数列 {an} 中,如果已知五个元素 a1, an,
n, d, Sn 中的任意三个, 请问: 能否求出其余两个量
结论:知 三 求 二
三、巩固新知
1.根据下列各题中的条件,求相应的等差数列{an}的Sn :
(1)a1=5,an=95,n=10
(2)a1=100,d=-2,n=50
500
2550
2.例6 已知数列{an}是等差数列:
(1)a1=7,a50=101,求S50
解:
计算
(1) 5+6+7+···+79+80
(2) 1+3+5+···+(2n-1)
(3)1-2+3-4+5-6+···+(2n-1)-2n
-n
3.变式练习
n2
3230
提示:n=76
4.例7. 已知一个等差数列{an}前10项的和是310,前20项的和是1220, 由这些条件能确定这个等差数列的首项和公差吗
1).已知在等差数列{an}中, ,.
求S7.
5.变式练习
2).求集合 的元素个
数,
并求这些元素的和.
解:
由 得
∴正整数 共有14个即 中共有14个元素
即:7,14,21,…,98 是以 为首项,
以 为末项的等差数列.
∴
5.变式练习
答案: 27
3).
4).等差数列-10,-6,-2,2,
…的前______项的和为54?
答案: n=9,或n=-3(舍去)
仍是知三求一
n2-6n-27=0
5.变式练习
5).已知一个共有n项的等差数列前4项之和为26,末四项之和为110,且所有项的和为187,求n.
n=11
提示:a1+a2+a3+a4=26
an+an-1+an-2+an-3=110
a1+an=34
5.变式练习
5.变式练习
知识打包 存放备用
an=a1+(n-1)d
对于Sn、an 、a1、n、d 五个量,“知三求二”.
方程(组)思想
(待定系数法)
倒序求和法
掌握与应用
1.等差数列前n项和的公式;
2.等差数列前n项和公式的推导方法
——倒序相加法;
3.在两个求和公式中,各有五个元素,只要
知道其中三个元素,结合通项公式就可
求出另两个元素.
(两个)
作业: 课本P24 习题 1题
四、课堂小结
4.2.2
等差数列的前n项的和(1)
选择性必修第二册 第四章 数列
学习目标
1.了解等差数列的前n项和公式发现的背景;
2.推导并掌握等差数列的前n项和公式;
3.能在具体的问题情境中,能运用等差数列的前n项和公式解决一些简单的数学问题和实际问题;
4.核心素养:数学建模、数学推理、数学运算。
高斯(Gauss,1777-1855),德国著名数学家,他研究的内容涉及数学的各个领域,被称为历史上最伟大的三位数学家之一,他与阿基米德、牛顿齐名,是数学史上一颗光芒四射的巨星,被誉为“数学王子”.
一、情景引入
有一次,老师与高斯去买铅笔,在商店发
现了一个堆放铅笔的V形架,
V形架的最下面一层放
一支铅笔,往上每一层
都比它下面一层多放一
支,最上面一层放100支.
老师问:高斯,你知道这
个V形架上共放着多少支铅笔吗?
问题1就是:
计算1+ 2+ 3 +… + 99 + 100
高斯的算法
计算: 1+ 2+ 3 +… + 99 + 100
高斯算法的高明之处在于他发现这100个数可以分为50组:
第一个数与最后一个数一组;
第二个数与倒数第二个数一组;
第三个数与倒数第三个数一组,……
每组数的和均相等,都等于101,50个101就等于5050了。高斯算法将加法问题转化为乘法运算,迅速准确得到了结果.
首尾配对相加法
中间的一组数是什么呢?
商店的一个堆放铅笔的V形架上最上面一层
若放101支.你知道这个V形架上共放着多少支铅笔吗?
问题2
问题就是:
计算:1+ 2+ 3 +… + 100 + 101
思路1(拿出中间项,再首尾配对)
原式=(1+101)+ (2+100)+ (3+99)+… + (50+52)+51
思路2(拿出末项,再首尾配对)
原式=(1+2+3+… + 100)+101
思路3(先凑成偶数项,再配对)原式=(1+2+3+… + 100+102)-102
思路3(先凑成偶数项,再配对)原式=0+1+2+3+… + 100+101
1.问题呈现
泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一。陵寝以宝石镶饰,图案之细致令人叫绝。
传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见左图),奢靡之程度,可见一斑。
你知道这个图案一共花了多少宝石吗?
二、探究新知
问题:图案中,第1层到第21层一共多少颗宝石?
这是求奇数个项和的问题,不能简单模仿偶数个项求和的办法,需要把中间项11看成首、尾两项1和21的等差中项。
通过前后比较得出认识:高斯“首尾配对” 的算法还得分奇、偶个项的情况求和。
有无简单的方法?
借助几何图形之直观性,把这个“全等三角形”倒置,与原图补成平行四边形。
问题:图案中,第1层到第21层一共多少颗宝石?
1
2
3
21
21
20
19
1
获得算法:
问题:图案中,第1层到第21层一共多少颗宝石?
探究了以上两个实际问题的求和,我们对数列求和有了一定的认识,那么能否将“倒序相加法”推广到任意一个等差数列呢?
这种方法不需分奇、偶个项的情况就可以求和, 很有创意,用数学式子表示就是:
1+ 2+ 3+ 4+……+21
21+20+19+18+……+1
对齐相加(其中下第二行的式子与第一行的
式子恰好是倒序)
这实质上是我们数学中一种求和的重要方法
倒序相加法
若V形架的的最下面一层放一支铅笔,往上每一层都比它下面一层
多放一支,最上面
一层有很多支铅笔,
老师说有n支。问:
这个V形架上共放
着多少支铅笔?
问题就是:
1+ 2+ 3 +… + (n-1) + n
若用首尾配对相加法,需要分类讨论.
三角形
平行四边形
倒序相加法
n + (n-1) + (n-2) +…+ 2 +1
那么,对一般的等差数列,如何求它的
前n项和呢?
分析:这其实是求一个具体的等差数列前n项和.
①
②
倒序相加法
已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .
如何才能将等式的右边化简?
①
②
倒序相加法
2.等差数列求和公式
等差数列的前n项和的公式:
思考:(1)公式的文字语言;
(2)公式的特点;
不含d
可知三求一
等差数列的前n项和等于首末两项的和与项数乘积的一半。
公式的记忆
我们可结合梯形的面积公式来记忆
等差数列前 n 项和公式.
n
a1
an
公式的记忆
a1
(n-1)d
n
a1
an
将图形分割成一个平行四边形和一个三角形.
我们可结合梯形的面积公式来记忆
等差数列前 n 项和公式.
在等差数列 {an} 中,如果已知五个元素 a1, an,
n, d, Sn 中的任意三个, 请问: 能否求出其余两个量
结论:知 三 求 二
三、巩固新知
1.根据下列各题中的条件,求相应的等差数列{an}的Sn :
(1)a1=5,an=95,n=10
(2)a1=100,d=-2,n=50
500
2550
2.例6 已知数列{an}是等差数列:
(1)a1=7,a50=101,求S50
解:
计算
(1) 5+6+7+···+79+80
(2) 1+3+5+···+(2n-1)
(3)1-2+3-4+5-6+···+(2n-1)-2n
-n
3.变式练习
n2
3230
提示:n=76
4.例7. 已知一个等差数列{an}前10项的和是310,前20项的和是1220, 由这些条件能确定这个等差数列的首项和公差吗
1).已知在等差数列{an}中, ,.
求S7.
5.变式练习
2).求集合 的元素个
数,
并求这些元素的和.
解:
由 得
∴正整数 共有14个即 中共有14个元素
即:7,14,21,…,98 是以 为首项,
以 为末项的等差数列.
∴
5.变式练习
答案: 27
3).
4).等差数列-10,-6,-2,2,
…的前______项的和为54?
答案: n=9,或n=-3(舍去)
仍是知三求一
n2-6n-27=0
5.变式练习
5).已知一个共有n项的等差数列前4项之和为26,末四项之和为110,且所有项的和为187,求n.
n=11
提示:a1+a2+a3+a4=26
an+an-1+an-2+an-3=110
a1+an=34
5.变式练习
5.变式练习
知识打包 存放备用
an=a1+(n-1)d
对于Sn、an 、a1、n、d 五个量,“知三求二”.
方程(组)思想
(待定系数法)
倒序求和法
掌握与应用
1.等差数列前n项和的公式;
2.等差数列前n项和公式的推导方法
——倒序相加法;
3.在两个求和公式中,各有五个元素,只要
知道其中三个元素,结合通项公式就可
求出另两个元素.
(两个)
作业: 课本P24 习题 1题
四、课堂小结
