人教A版(2019)高二数学选择性必修第二册课件 5.3.2.2 函数的最大(小)值(共23张PPT)
文档属性
| 名称 | 人教A版(2019)高二数学选择性必修第二册课件 5.3.2.2 函数的最大(小)值(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 860.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-10 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
5.3.2-2
函数的最大(小)值
选择性必修 第二册 第五章 一元函数的导数及其应用
学习目标
1.理解最值的概念, 了解函数最值与极值的区别和联系;
2.会利用导数求在给定区间上次数不超过三次的函数的最大值与最小值.
3.核心素养:直观想象、数学抽象、数学运算。
求解函数极值的一般步骤:
(1)确定函数的定义域
(2)求函数的导数f ,(x)
(3)求方程f ,(x)=0的根
(4)用方程f ,(x)=0的根,顺次将函数的定义
域分成若干个开区间,并列成表格
(5)由f ,(x)在方程f ,(x)=0的根左右的符号,
来判断f(x)在这个根处取极值的情况
一、回顾旧知
在社会生活实践中,为了发挥最大的经济效益,常常遇到如何能使用料最省、产量最高,效益最大等问题,这些问题的解决常常可转化为求一个函数的最大值和最小值问题.
函数在什么条件下一定有最大、最小值
他们与函数极值关系如何?
极值是一个局部概念,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小.
二、探究新知
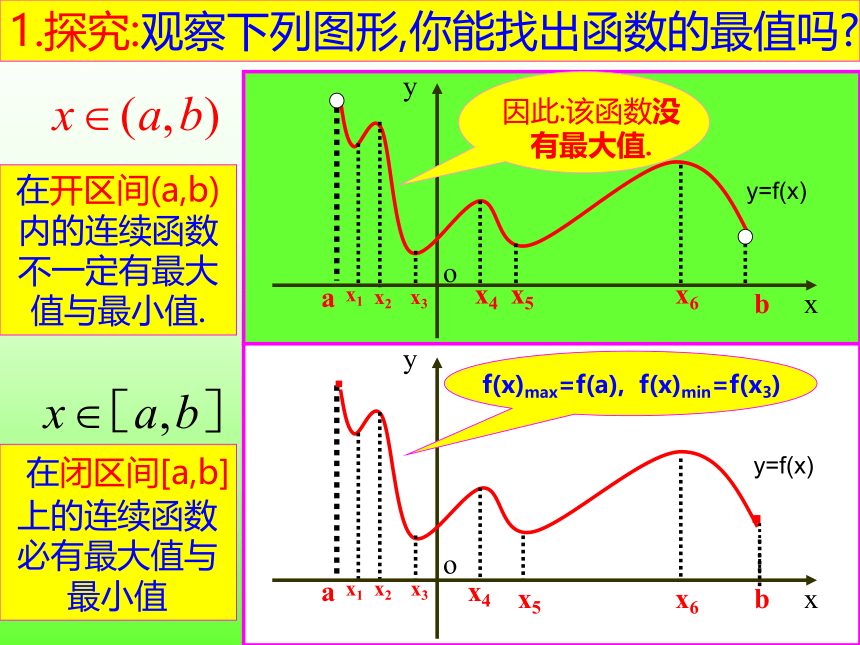
1.探究:观察下列图形,你能找出函数的最值吗
x
o
y
a
x1
b
y=f(x)
x2
x3
x4
x5
x6
x
o
y
a
x1
b
y=f(x)
x2
x3
x4
x5
x6
在开区间(a,b)内的连续函数不一定有最大值与最小值.
在闭区间[a,b]上的连续函数必有最大值与最小值
因此:该函数没有最大值.
f(x)max=f(a), f(x)min=f(x3)
·
·
x
o
y
a
x1
b
y=f(x)
x2
x3
x4
x5
x6
2.如何求出函数在[a,b]上的最值?
一般的如果在区间,[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.
·
·
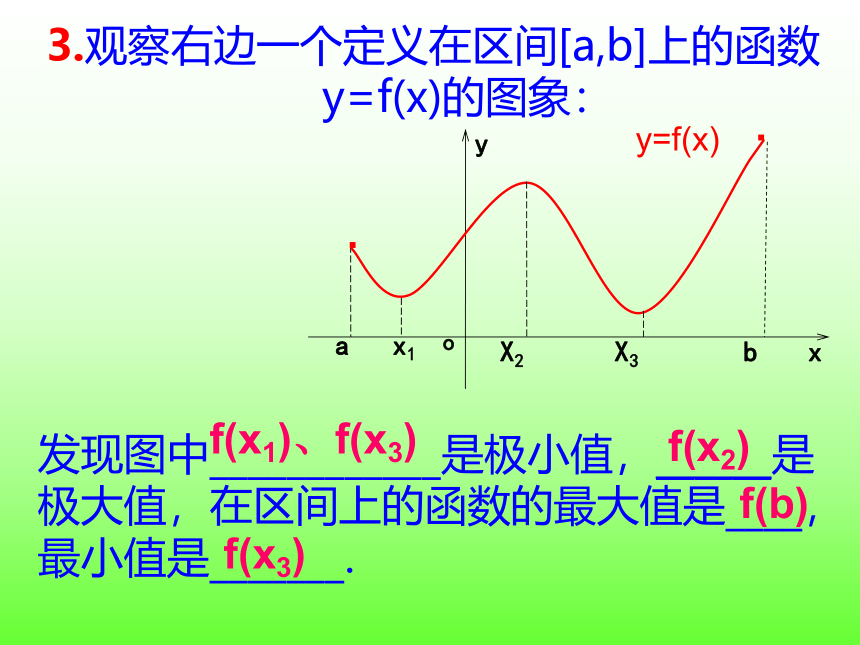
3.观察右边一个定义在区间[a,b]上的函数
y=f(x)的图象:
发现图中____________是极小值,______是极大值,在区间上的函数的最大值是____,最小值是_______.
f(x1)、f(x3)
f(x2)
f(b)
f(x3)
x
X2
o
a
X3
b
x1
y
y=f(x)
·
·
(2) 将y=f(x)的各极值与f(a),f(b)(端点处) 比较,其中最大的一个为最大值,最小的一个最小值.
4. 求f(x)在闭区间[a,b]上的最值的步骤:
(1) 求f(x)在区间(a,b)内极值(极大值或极小值)
注意:
1.在定义域内, 最值唯一;极值不唯一;
2.最大值一定比最小值大.
解:
三、运用新知
1.例1.
当x=2时有极小值,
1.求出所有导数为0的点;
2.计算端点值;
3.比较确定最值
函数 y = x + 3 x -9x在 [-4 , 4 ]上的
最大值为 ,最小值为 .
解:由 f (x)=3x +6x-9=0,
f (-4) =20 , f (4) =76
得x1=-3,x2=1
f (-3)=27, f (1)=-5
76
-5
比较以上各函数值,可知函数在[-4 , 4 ]上的
最大值为 f (4) =76,最小值为 f (1)=-5.
2.变式训练1
已知函数
(2)求函数 在区间 上最值.
(1)求曲线 在点 处的切线方程;
3.变式训练2
4.拓展提高
1.我们知道,如果在闭区间[a,b]上函数y=f(x)的图像是一条连续不断的曲线,那么它必定有最大值和最小值:那么把闭区间[a,b]换成开区间(a,b)是否一定有最值呢? 如下图:
不一定
2.函数f(x)有一个极值点时,极值点必定是最值点.
3. 如果函数f(x)在开区间(a,b)上只有一个极值点,那么这个极值点必定是最值点.
有两个极值点时,函数有无最值情况不定。
5.例2.
设函数
6.变式训练3
内的最小值.
7.求函数的最值时,应注意以下几点:
(1).函数的极值是在局部范围内讨论问题,是一个局 部概念,而函数的最值是对整个定义域而言,是在整体范围内讨论问题,是一个整体性的概念.
(2).闭区间[a,b]上的连续函数一定有最值.开区间(a,b)内的可导函数不一定有最值,但若有唯一的极值,则此极值必是函数的最值.
(3).函数在其定义域上的最大值与最小值至多各有一个, 而函数的极值则可能不止一个,也可能没有极值,并且极大值(极小值)不一定就是最大值(最小值).
8.例3.
解:
9.变式训练4
解:
10.例5.已知函数
其中,
(1)求函数f(x)的单调区间;
函数f(x)在[1,2]上的最大值
为M,最小值为N,求M-N的取值范围.
解:(2)由 及(1)知,f(x)在[1,2a]内是减函数,在[2a,2]内是增函数,
所以g(a)在 内是减函数.
所以M-N的取值范围是:
已知函数
(1)求函数f(x)的单调区间;
(2)当a>0时,求函数f(x)在[1,2]上的最小值.
解: 当 ,即 函数f(x)在[1,2]上是减函数, 所以f(x)的最小值是
11.变式训练5
当 ,即 函数f(x)在[1,2]上是增函数, 所以f(x)的最小值是
当 ,即 函数f(x)在 上是增函数, 在 是减函数,又
当 时f(x)的最小值是
综上可知
f(x)的最小值是-a;
f(x)的最小值是
所以当 时f(x)的最小值
(2) 将y=f(x)的各极值与f(a),f(b)(端点处)比较,
其中最大的一个为最大值,最小的 一个最
小值.
1.求f(x)在闭区间[a,b]上的最值的步骤:
(1) 求f(x)在区间(a,b)内极值(极大值或极小值)
四、课堂小结
2.求函数最值的一般方法
1).是利用函数性质;
2).是利用不等式;
3).是利用导数.
作业: 课本P98 习题5.3 6,12题
5.3.2-2
函数的最大(小)值
选择性必修 第二册 第五章 一元函数的导数及其应用
学习目标
1.理解最值的概念, 了解函数最值与极值的区别和联系;
2.会利用导数求在给定区间上次数不超过三次的函数的最大值与最小值.
3.核心素养:直观想象、数学抽象、数学运算。
求解函数极值的一般步骤:
(1)确定函数的定义域
(2)求函数的导数f ,(x)
(3)求方程f ,(x)=0的根
(4)用方程f ,(x)=0的根,顺次将函数的定义
域分成若干个开区间,并列成表格
(5)由f ,(x)在方程f ,(x)=0的根左右的符号,
来判断f(x)在这个根处取极值的情况
一、回顾旧知
在社会生活实践中,为了发挥最大的经济效益,常常遇到如何能使用料最省、产量最高,效益最大等问题,这些问题的解决常常可转化为求一个函数的最大值和最小值问题.
函数在什么条件下一定有最大、最小值
他们与函数极值关系如何?
极值是一个局部概念,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小.
二、探究新知
1.探究:观察下列图形,你能找出函数的最值吗
x
o
y
a
x1
b
y=f(x)
x2
x3
x4
x5
x6
x
o
y
a
x1
b
y=f(x)
x2
x3
x4
x5
x6
在开区间(a,b)内的连续函数不一定有最大值与最小值.
在闭区间[a,b]上的连续函数必有最大值与最小值
因此:该函数没有最大值.
f(x)max=f(a), f(x)min=f(x3)
·
·
x
o
y
a
x1
b
y=f(x)
x2
x3
x4
x5
x6
2.如何求出函数在[a,b]上的最值?
一般的如果在区间,[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.
·
·
3.观察右边一个定义在区间[a,b]上的函数
y=f(x)的图象:
发现图中____________是极小值,______是极大值,在区间上的函数的最大值是____,最小值是_______.
f(x1)、f(x3)
f(x2)
f(b)
f(x3)
x
X2
o
a
X3
b
x1
y
y=f(x)
·
·
(2) 将y=f(x)的各极值与f(a),f(b)(端点处) 比较,其中最大的一个为最大值,最小的一个最小值.
4. 求f(x)在闭区间[a,b]上的最值的步骤:
(1) 求f(x)在区间(a,b)内极值(极大值或极小值)
注意:
1.在定义域内, 最值唯一;极值不唯一;
2.最大值一定比最小值大.
解:
三、运用新知
1.例1.
当x=2时有极小值,
1.求出所有导数为0的点;
2.计算端点值;
3.比较确定最值
函数 y = x + 3 x -9x在 [-4 , 4 ]上的
最大值为 ,最小值为 .
解:由 f (x)=3x +6x-9=0,
f (-4) =20 , f (4) =76
得x1=-3,x2=1
f (-3)=27, f (1)=-5
76
-5
比较以上各函数值,可知函数在[-4 , 4 ]上的
最大值为 f (4) =76,最小值为 f (1)=-5.
2.变式训练1
已知函数
(2)求函数 在区间 上最值.
(1)求曲线 在点 处的切线方程;
3.变式训练2
4.拓展提高
1.我们知道,如果在闭区间[a,b]上函数y=f(x)的图像是一条连续不断的曲线,那么它必定有最大值和最小值:那么把闭区间[a,b]换成开区间(a,b)是否一定有最值呢? 如下图:
不一定
2.函数f(x)有一个极值点时,极值点必定是最值点.
3. 如果函数f(x)在开区间(a,b)上只有一个极值点,那么这个极值点必定是最值点.
有两个极值点时,函数有无最值情况不定。
5.例2.
设函数
6.变式训练3
内的最小值.
7.求函数的最值时,应注意以下几点:
(1).函数的极值是在局部范围内讨论问题,是一个局 部概念,而函数的最值是对整个定义域而言,是在整体范围内讨论问题,是一个整体性的概念.
(2).闭区间[a,b]上的连续函数一定有最值.开区间(a,b)内的可导函数不一定有最值,但若有唯一的极值,则此极值必是函数的最值.
(3).函数在其定义域上的最大值与最小值至多各有一个, 而函数的极值则可能不止一个,也可能没有极值,并且极大值(极小值)不一定就是最大值(最小值).
8.例3.
解:
9.变式训练4
解:
10.例5.已知函数
其中,
(1)求函数f(x)的单调区间;
函数f(x)在[1,2]上的最大值
为M,最小值为N,求M-N的取值范围.
解:(2)由 及(1)知,f(x)在[1,2a]内是减函数,在[2a,2]内是增函数,
所以g(a)在 内是减函数.
所以M-N的取值范围是:
已知函数
(1)求函数f(x)的单调区间;
(2)当a>0时,求函数f(x)在[1,2]上的最小值.
解: 当 ,即 函数f(x)在[1,2]上是减函数, 所以f(x)的最小值是
11.变式训练5
当 ,即 函数f(x)在[1,2]上是增函数, 所以f(x)的最小值是
当 ,即 函数f(x)在 上是增函数, 在 是减函数,又
当 时f(x)的最小值是
综上可知
f(x)的最小值是-a;
f(x)的最小值是
所以当 时f(x)的最小值
(2) 将y=f(x)的各极值与f(a),f(b)(端点处)比较,
其中最大的一个为最大值,最小的 一个最
小值.
1.求f(x)在闭区间[a,b]上的最值的步骤:
(1) 求f(x)在区间(a,b)内极值(极大值或极小值)
四、课堂小结
2.求函数最值的一般方法
1).是利用函数性质;
2).是利用不等式;
3).是利用导数.
作业: 课本P98 习题5.3 6,12题
