人教A版(2019)高二数学选择性必修第二册课件 5.3.2.1 函数的极值(共21张PPT)
文档属性
| 名称 | 人教A版(2019)高二数学选择性必修第二册课件 5.3.2.1 函数的极值(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-10 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
5.3.2-1
函 数 的 极 值
选择性必修 第二册 第五章 一元函数的导数及其应用
学习目标
1.了解函数极值的概念,结合函数的图象了解在某点取得极值的必要条件和充分条件;
2.会用导数求次数不超过三次的函数的极大值、极小值.
3.核心素养:直观想象、数学抽象、数学运算。
1.函数单调性与导数的关系
一、回顾旧知
二、探究新知
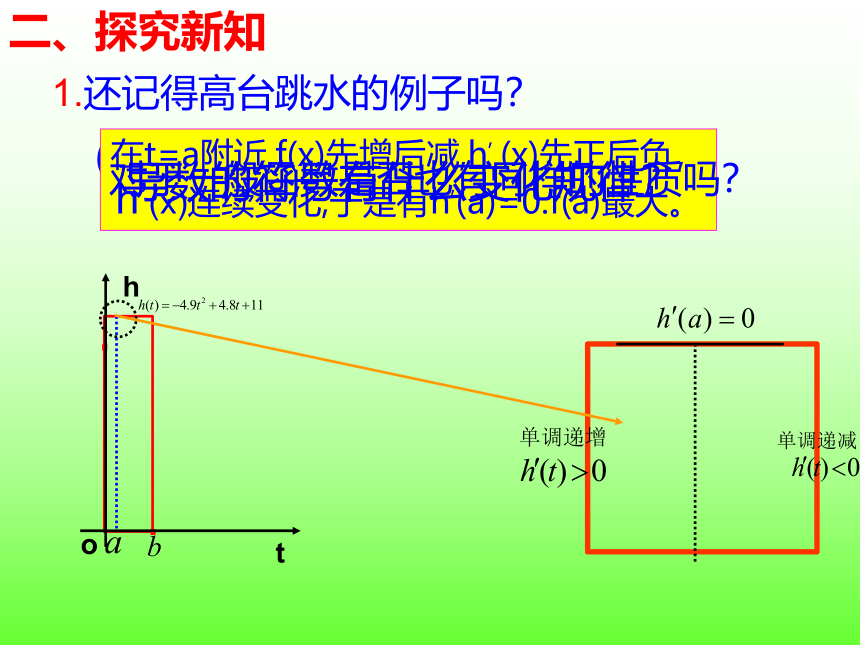
1.还记得高台跳水的例子吗?
h
t
o
(1)当t=a时运动员距水面高度最大,
h(t)在此点的导数是多少呢?
(2)当t(3)当t>a时h(t)的单调性是怎样的呢?
导数的符号有什么变化规律?
在t=a附近,f(x)先增后减,h, (x)先正后负,
h’(x)连续变化,于是有h,(a)=0.f(a)最大。
导数的符号有什么变化规律?
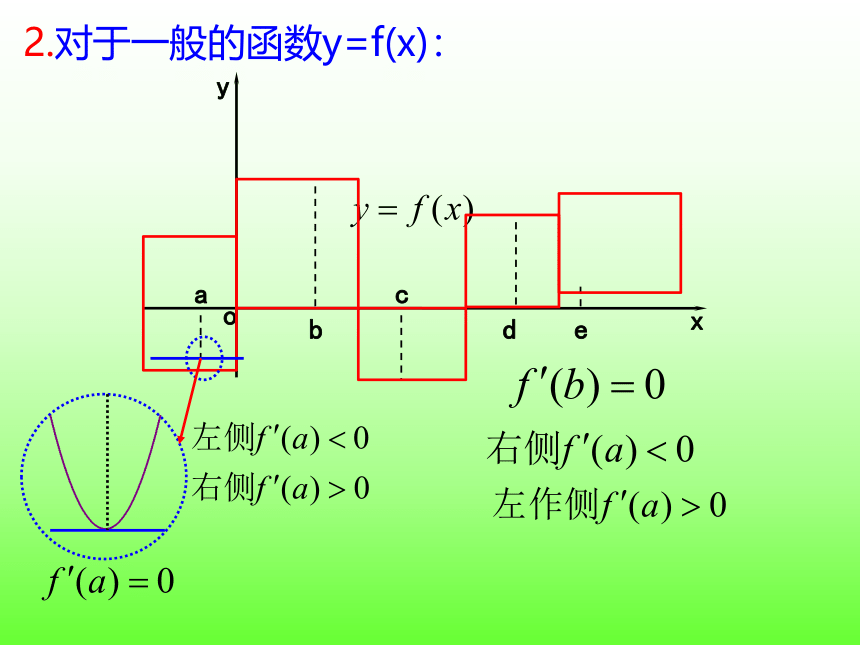
对于一般函数是否也有同样的性质吗?
o
a
c
b
x
y
d
e
2.对于一般的函数y=f(x):
o
a
c
b
x
y
d
e
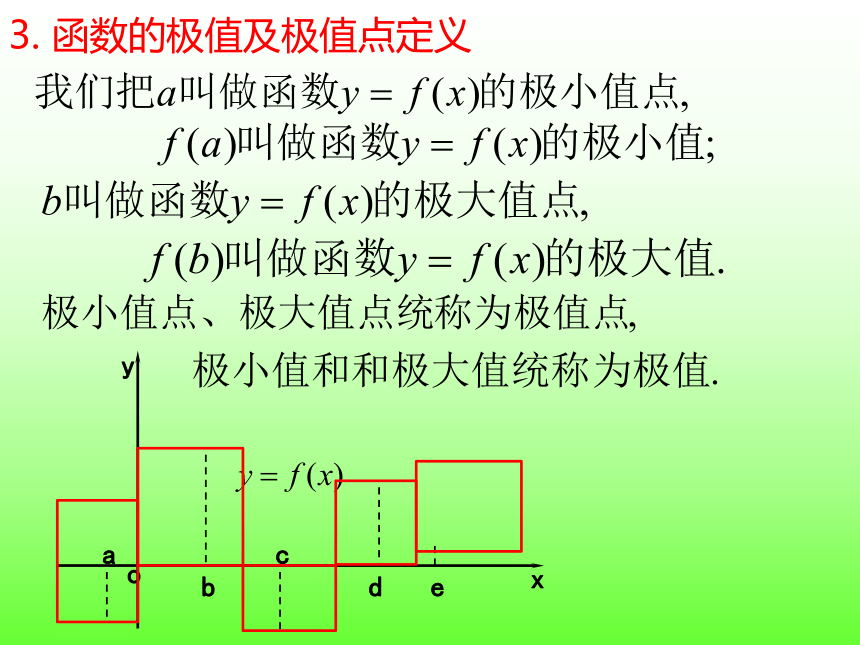
3. 函数的极值及极值点定义
解:
x (-∞,-2) -2 (-2,2) 2 (2,+∞)
因此,当x=-2时有极大值
三、巩固新知
1.例1.
当x=2时有极小值,
+
0
-
0
+
↗
极大值
↘
极小值
↗
解:
当x变化时, ,y的变化情况如下表:
x (-∞,-1) -1 (-1,1) 1 (1,+∞)
y’ - 0 + 0 -
y ↘ 极小值-3 ↗ 极大值3 ↘
因此,当x=1时有极大值,并且,y极大值=3;
而,当x=-1时有极小值,并且,y极小值=- 3.
2.变式训练1
解:
2.变式训练1
3.求解函数极值的一般步骤:
(1)求函数的定义域;
左正右负极大值;
左负右正极小值.
可导函数的极值点一定是它导数为零的点,反之函数的导数为零的点,不一定是该函数的极值点.例如,函数y=x3,在点x=0处的导数为零,但它不是极值点,原因是函数在点x=0处左右两侧的导数都大于零.
因此导数为零的点仅是该点为极值点的必要条件,
其充分条件是在这点两侧的导数异号.
4.思考:导数值为0的点一定是函数的极值点吗
解:
解:
↗
↗
↘
6.变式训练2
7.例3:求函数 的极值.
解:函数的定义域为:
x (-∞,-a) -a (-a,0) (0,a) a (a,+∞)
f’(x) + 0 - - 0 +
f(x) ↗ 极大值-2a ↘ ↘ 极小值2a ↗
故当x=-a时,f(x)有极大值f(-a)=-2a;
当x=a时,f(x)有极小值f(a)=2a.
7.例3:求函数 的极值.
令 ,解得x1=-a,x2=a, (-a当x变化时, ,f(x) 的变化情况如下表:
x (-∞,a) a (a,0) (0,-a) -a (-a,+∞)
f’(x) + 0 - - 0 +
f(x) ↗ 极大值2a ↘ ↘ 极小值-2a ↗
故当x=a时,f(x)有极大值f(a)=2a;
当x=-a时,f(x)有极小值f(-a)=-2a.
7.例3:求函数 的极值.
令 ,解得x1=-a,x2=a ,(a<-a)
当x变化时, ,f(x)的变化情况如下表:
无极值
8.变式训练3
9.变式训练4
设函数 其中
处的切线的斜率;
(1)当 时,求曲线 在点
(2)求函数 的单调区间与极值.
o
a
c
b
x
y
d
e
四、课堂小结
2.求解函数极值的一般步骤:
(1)求函数的定义域;
左正右负极大值;
左负右正极小值.
作业: 课本P98 习题5.2 5②④
5.3.2-1
函 数 的 极 值
选择性必修 第二册 第五章 一元函数的导数及其应用
学习目标
1.了解函数极值的概念,结合函数的图象了解在某点取得极值的必要条件和充分条件;
2.会用导数求次数不超过三次的函数的极大值、极小值.
3.核心素养:直观想象、数学抽象、数学运算。
1.函数单调性与导数的关系
一、回顾旧知
二、探究新知
1.还记得高台跳水的例子吗?
h
t
o
(1)当t=a时运动员距水面高度最大,
h(t)在此点的导数是多少呢?
(2)当t
导数的符号有什么变化规律?
在t=a附近,f(x)先增后减,h, (x)先正后负,
h’(x)连续变化,于是有h,(a)=0.f(a)最大。
导数的符号有什么变化规律?
对于一般函数是否也有同样的性质吗?
o
a
c
b
x
y
d
e
2.对于一般的函数y=f(x):
o
a
c
b
x
y
d
e
3. 函数的极值及极值点定义
解:
x (-∞,-2) -2 (-2,2) 2 (2,+∞)
因此,当x=-2时有极大值
三、巩固新知
1.例1.
当x=2时有极小值,
+
0
-
0
+
↗
极大值
↘
极小值
↗
解:
当x变化时, ,y的变化情况如下表:
x (-∞,-1) -1 (-1,1) 1 (1,+∞)
y’ - 0 + 0 -
y ↘ 极小值-3 ↗ 极大值3 ↘
因此,当x=1时有极大值,并且,y极大值=3;
而,当x=-1时有极小值,并且,y极小值=- 3.
2.变式训练1
解:
2.变式训练1
3.求解函数极值的一般步骤:
(1)求函数的定义域;
左正右负极大值;
左负右正极小值.
可导函数的极值点一定是它导数为零的点,反之函数的导数为零的点,不一定是该函数的极值点.例如,函数y=x3,在点x=0处的导数为零,但它不是极值点,原因是函数在点x=0处左右两侧的导数都大于零.
因此导数为零的点仅是该点为极值点的必要条件,
其充分条件是在这点两侧的导数异号.
4.思考:导数值为0的点一定是函数的极值点吗
解:
解:
↗
↗
↘
6.变式训练2
7.例3:求函数 的极值.
解:函数的定义域为:
x (-∞,-a) -a (-a,0) (0,a) a (a,+∞)
f’(x) + 0 - - 0 +
f(x) ↗ 极大值-2a ↘ ↘ 极小值2a ↗
故当x=-a时,f(x)有极大值f(-a)=-2a;
当x=a时,f(x)有极小值f(a)=2a.
7.例3:求函数 的极值.
令 ,解得x1=-a,x2=a, (-a
x (-∞,a) a (a,0) (0,-a) -a (-a,+∞)
f’(x) + 0 - - 0 +
f(x) ↗ 极大值2a ↘ ↘ 极小值-2a ↗
故当x=a时,f(x)有极大值f(a)=2a;
当x=-a时,f(x)有极小值f(-a)=-2a.
7.例3:求函数 的极值.
令 ,解得x1=-a,x2=a ,(a<-a)
当x变化时, ,f(x)的变化情况如下表:
无极值
8.变式训练3
9.变式训练4
设函数 其中
处的切线的斜率;
(1)当 时,求曲线 在点
(2)求函数 的单调区间与极值.
o
a
c
b
x
y
d
e
四、课堂小结
2.求解函数极值的一般步骤:
(1)求函数的定义域;
左正右负极大值;
左负右正极小值.
作业: 课本P98 习题5.2 5②④
