人教版七年级数学下册课件:5.1.1相交线(共21张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件:5.1.1相交线(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-10 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
第1课时 相交线
第五章 相交线与平行线
01
学习目标
02
知识要点
03
对点训练
04
精典范例
05
变式练习
1.(2022新课标)理解对顶角、补角等概念.
2.(2022新课标)探索并掌握对顶角相等的性质.
3.通过在图形中辨认对顶角、邻补角,培养学生的识图能力.
几何直观 推理能力
模型观念 应用意识
知识点一:邻补角及其性质
(1)定义:
两个角有一条公共边,它们的另一边互为反向延长线,具有这种位置关系的两个角,互为 .
(2)性质:邻补角 .
几何语言:
∵如图,∠1与∠2是邻补角,
∴ .
∠1+∠2=180°
互补
邻补角
(3)温馨提示:互为邻补角的两个角一定互补,但互补的两个角不一定是邻补角.
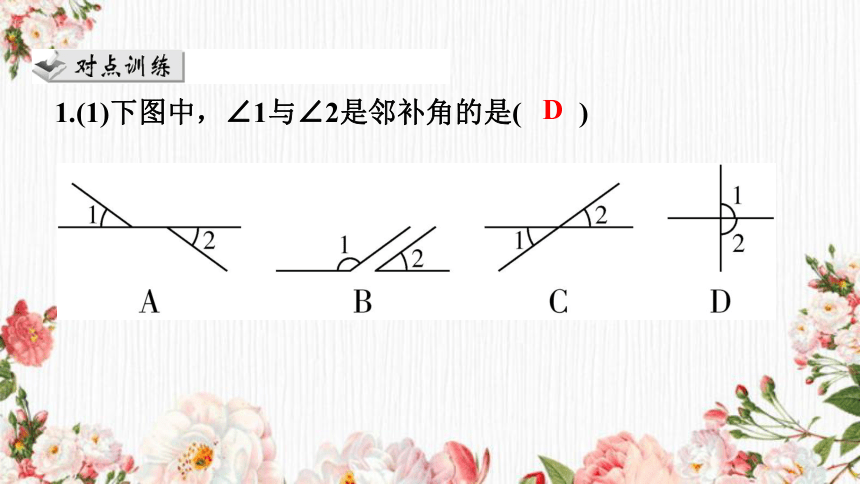
1.(1)下图中,∠1与∠2是邻补角的是( )
D
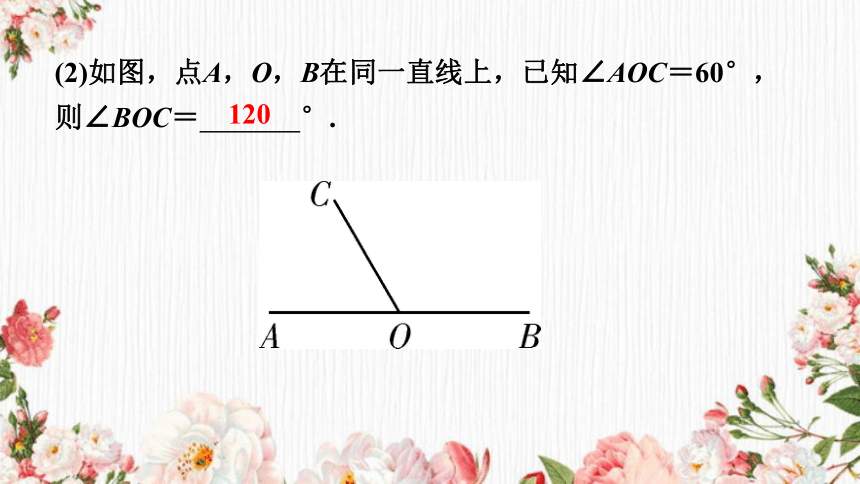
(2)如图,点A,O,B在同一直线上,已知∠AOC=60°,则∠BOC= °.
120
知识点二:对顶角及其性质
(1)定义:
有一个公共顶点,并且其中一个角的两边是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为
.
(2)性质:对顶角 .
几何语言:
∵如图,∠1与∠2是对顶角,
∴ .
∠1=∠2
相等
对顶角
(3)温馨提示:对顶角相等,但相等的角不一定是对顶角.
2.(1)下图中,∠1和∠2是对顶角的是( )
B
(2)(人教7下P9、北师7下P39)(2022北京改编)如图是对顶角量角器,用它测量角的原理是 .
对顶角相等
(3)如图,两直线交于点O,若∠1+∠2=76°,
则∠1= °.
38
3.【例1】(核心教材母题:人教7下P3、北师7下P40)如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数.
解:由邻补角的定义,得
∠2=180°-∠1=180°-40°=140°.
由对顶角相等,得∠3=∠1=40°,∠4=∠2=140°.
核心教材母题:教材是新中考命题的依据,近年来广东省中考数学卷中都有较多题的素材来源于人教版和北师大版.本书将两个版本重合的教材母题进行汇总,并作为课堂例习题呈现.
7.如图,AB与CD相交于一点,若∠2+∠4=140°,则∠1= °,∠4= °.
70
110
4.【例2】(人教7下P8)如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC=70°,求∠BOD的度数.
解:∵OA平分∠EOC,
∴∠AOE=∠AOC,
∵∠EOC=70°,
∴∠AOC=35°,
∴∠BOD=∠AOC=35°.
8.如图,直线AB,CD相交于点O,OE是∠AOD的平分线,∠AOC=50°.
(1)求∠AOD的度数;
(2)求∠DOE的度数.
解:(1)∵∠AOC=50°,
∴∠AOD=180°-∠AOC=130°.
(2)∵OE是∠AOD的平分线,
∴∠DOE=∠AOD=65°.
5.【例3】如图,AB,CD相交于点O,∠2=2∠1,求∠3的度数.
解:∵∠1+∠2=180°,∠2=2∠1,
∴∠1+∠2=∠1+2∠1=180°,
∴∠1=60°,∴∠3=∠1=60°.
9.如图,a,b相交于点O,∠1∶∠2=1∶3,求∠2和∠3的度数.
解:∵∠1+∠2=180°,∠1∶∠2=1∶3,
∴∠1+∠2=∠1+3∠1=4∠1=180°,
∴∠1=45°,∴∠2=135°,∠3=45°.
解:∵∠BOC+∠AOC=180°,∠BOC=2∠AOC,
∴2∠AOC+∠AOC=180°,
∴3∠AOC=180°,∴∠AOC=60°,
∵∠AOE=15°,
∴∠EOC=∠AOC-∠AOE=60°-15°=45°,
∴∠DOF=∠EOC=45°.
6.【例4】如图,直线AB,CD,EF相交于点O,且∠AOE=15°,∠BOC=2∠AOC,求∠DOF的度数.
★10.(人教7下P8改编)如图,AB,CD相交于点O,OE平分∠BOC,∠AOC∶∠AOD=2∶3,求∠BOE的度数.
解:∵∠AOC+∠AOD=180°,∠AOC∶∠AOD=2∶3,
∴∠AOC+∠AOD=∠AOD+∠AOD=∠AOD=180°,
∴∠AOD=108°,∴∠BOC=108°,
∵OE平分∠BOC,∴∠BOE=∠COE=54°.
备注:每课时带★的题目为提高题.
第1课时 相交线
第五章 相交线与平行线
01
学习目标
02
知识要点
03
对点训练
04
精典范例
05
变式练习
1.(2022新课标)理解对顶角、补角等概念.
2.(2022新课标)探索并掌握对顶角相等的性质.
3.通过在图形中辨认对顶角、邻补角,培养学生的识图能力.
几何直观 推理能力
模型观念 应用意识
知识点一:邻补角及其性质
(1)定义:
两个角有一条公共边,它们的另一边互为反向延长线,具有这种位置关系的两个角,互为 .
(2)性质:邻补角 .
几何语言:
∵如图,∠1与∠2是邻补角,
∴ .
∠1+∠2=180°
互补
邻补角
(3)温馨提示:互为邻补角的两个角一定互补,但互补的两个角不一定是邻补角.
1.(1)下图中,∠1与∠2是邻补角的是( )
D
(2)如图,点A,O,B在同一直线上,已知∠AOC=60°,则∠BOC= °.
120
知识点二:对顶角及其性质
(1)定义:
有一个公共顶点,并且其中一个角的两边是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为
.
(2)性质:对顶角 .
几何语言:
∵如图,∠1与∠2是对顶角,
∴ .
∠1=∠2
相等
对顶角
(3)温馨提示:对顶角相等,但相等的角不一定是对顶角.
2.(1)下图中,∠1和∠2是对顶角的是( )
B
(2)(人教7下P9、北师7下P39)(2022北京改编)如图是对顶角量角器,用它测量角的原理是 .
对顶角相等
(3)如图,两直线交于点O,若∠1+∠2=76°,
则∠1= °.
38
3.【例1】(核心教材母题:人教7下P3、北师7下P40)如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数.
解:由邻补角的定义,得
∠2=180°-∠1=180°-40°=140°.
由对顶角相等,得∠3=∠1=40°,∠4=∠2=140°.
核心教材母题:教材是新中考命题的依据,近年来广东省中考数学卷中都有较多题的素材来源于人教版和北师大版.本书将两个版本重合的教材母题进行汇总,并作为课堂例习题呈现.
7.如图,AB与CD相交于一点,若∠2+∠4=140°,则∠1= °,∠4= °.
70
110
4.【例2】(人教7下P8)如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC=70°,求∠BOD的度数.
解:∵OA平分∠EOC,
∴∠AOE=∠AOC,
∵∠EOC=70°,
∴∠AOC=35°,
∴∠BOD=∠AOC=35°.
8.如图,直线AB,CD相交于点O,OE是∠AOD的平分线,∠AOC=50°.
(1)求∠AOD的度数;
(2)求∠DOE的度数.
解:(1)∵∠AOC=50°,
∴∠AOD=180°-∠AOC=130°.
(2)∵OE是∠AOD的平分线,
∴∠DOE=∠AOD=65°.
5.【例3】如图,AB,CD相交于点O,∠2=2∠1,求∠3的度数.
解:∵∠1+∠2=180°,∠2=2∠1,
∴∠1+∠2=∠1+2∠1=180°,
∴∠1=60°,∴∠3=∠1=60°.
9.如图,a,b相交于点O,∠1∶∠2=1∶3,求∠2和∠3的度数.
解:∵∠1+∠2=180°,∠1∶∠2=1∶3,
∴∠1+∠2=∠1+3∠1=4∠1=180°,
∴∠1=45°,∴∠2=135°,∠3=45°.
解:∵∠BOC+∠AOC=180°,∠BOC=2∠AOC,
∴2∠AOC+∠AOC=180°,
∴3∠AOC=180°,∴∠AOC=60°,
∵∠AOE=15°,
∴∠EOC=∠AOC-∠AOE=60°-15°=45°,
∴∠DOF=∠EOC=45°.
6.【例4】如图,直线AB,CD,EF相交于点O,且∠AOE=15°,∠BOC=2∠AOC,求∠DOF的度数.
★10.(人教7下P8改编)如图,AB,CD相交于点O,OE平分∠BOC,∠AOC∶∠AOD=2∶3,求∠BOE的度数.
解:∵∠AOC+∠AOD=180°,∠AOC∶∠AOD=2∶3,
∴∠AOC+∠AOD=∠AOD+∠AOD=∠AOD=180°,
∴∠AOD=108°,∴∠BOC=108°,
∵OE平分∠BOC,∴∠BOE=∠COE=54°.
备注:每课时带★的题目为提高题.
