人教版七年级数学下册课件:5.1.2垂线(1)(共19张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件:5.1.2垂线(1)(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-10 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
垂线(1)
第五章 相交线与平行线
01
学习目标
02
知识要点
03
对点训练
04
精典范例
05
变式练习
1.(2022新课标)理解垂线的概念,能用三角板或量角器过一点画已知直线的垂线.
2.(2022新课标)掌握基本事实:同一平面内,过一点有且只有一条直线与已知直线垂直.
几何直观 空间观念
推理能力 应用意识
知识点一:垂线
(1)定义:
直线AB与CD相交于点O,若∠AOD=90°,则这两条直线互相 ,记作AB⊥CD(或CD⊥AB),点O叫做垂足.
(2)图示:
垂直
(3)几何语言:
∵∠AOD=90°,∴AB CD.
(4)垂直是相交的一种特殊情形.
(5)画垂线.
⊥
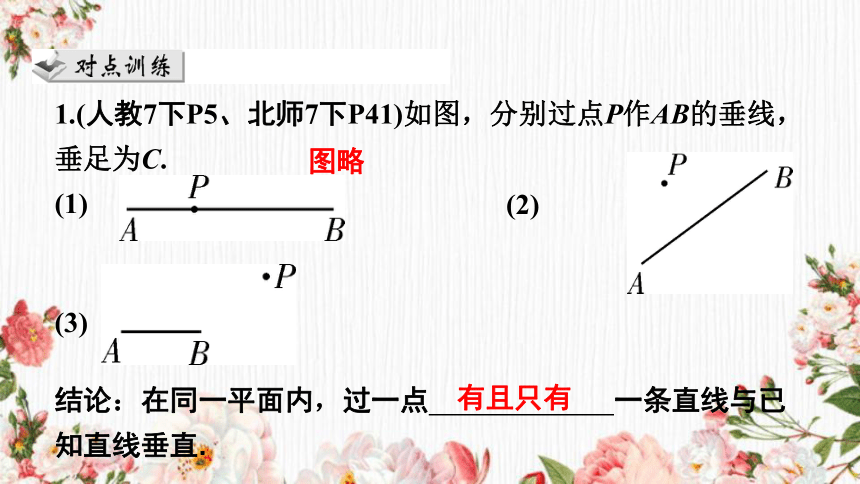
结论:在同一平面内,过一点 一条直线与已知直线垂直.
(3)
有且只有
(2)
1.(人教7下P5、北师7下P41)如图,分别过点P作AB的垂线,垂足为C.
(1)
图略
(3)几何语言:
∵AB⊥CD,
∴∠AOC=∠AOD=∠BOD=∠BOC= °.
知识点二:垂线的性质
(1)垂线的性质:
两直线垂直,则它们的夹角为 °.
(2)图示:
90
90
2.(1)如图,OA⊥OB,∠1=35°,求∠2的度数;
解:(1)∵OA⊥OB,∴∠AOB=90°,
∵∠1=35°,∴∠2=∠AOB-∠1=90°-35°=55°.
(2)如图,OA⊥OB,∠BOC=130°,求∠1的度数.
解:(2)∵OA⊥OB,∴∠AOB=90°,
∵∠BOC=130°,∴∠1=∠BOC-∠AOB=130°-90°=40°.
3.【例1】(人教7下P8)如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,求∠AOD的度数.
解:∵EO⊥AB,
∴∠BOE=90°,
∵∠EOC=35°,
∴∠BOC=∠BOE+∠EOC=125°.
∴∠AOD=∠BOC=125°.
7.(2022河南)如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,求∠2的度数.
解:∵EO⊥CD,∴∠COE=90°,
∵∠1+∠COE+∠2=180°,
∴∠2=180°-∠1-∠COE=180°-54°-90°=36°.
4.【例2】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,求∠CON的度数.
解:∵OM平分∠AOC,∠AOM=35°,
∴∠COM=∠AOM=35°,
∵ON⊥OM,∴∠MON=90°.
∴∠CON=∠MON-∠MOC=90°-35°=55°.
8.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,∠BOD=35°,求∠CON的度数.
解:∵∠BOD=35°,∴∠AOC=∠BOD=35°,
∵OM平分∠AOC,
∴∠COM=∠AOC=17.5°.
∵ON⊥OM,∴∠MON=90°,
∴∠CON=∠MON-∠COM=90°-17.5°=72.5°.
5.【例3】如图,分别过点A,B画OB,OA的垂线.
图略
9.如图,已知∠AOB和OA上一点P.
(1)过点P画PC⊥OA,交OB于点C;
(2)过点P画PD⊥OB,垂足是点D.
图略
6.【例4】如图,O为直线AB上一点,且∠BOC=3∠AOC,OC平分∠AOD.
(1)求∠AOC的度数;
(2)判断OD与AB的位置关系,并说明理由.
解:(1)∵∠BOC=3∠AOC,∠AOC+∠BOC=180°,
∴∠AOC+3∠AOC=180°,解得∠AOC=45°.
(2)OD⊥AB.理由如下:∵OC平分∠AOD,
∴∠AOD=2∠AOC=2×45°=90°,∴OD⊥AB.
(2)若∠AOD=30°,求证:OC为∠AOE的平分线;
(3)若∠AOD∶∠AOE=2∶11,则∠BOE的度数为
.
★10.如图,O为直线AB上一点,OC为射线,OD,OE分别为∠AOC,∠BOC的平分线.
(1)判断射线OD,OE的位置关系,说明理由;
(1)解:垂直,理由如下:
∵OD,OE分别为∠AOC,∠BOC的平分线,
∴∠COD=∠COA,∠COE=∠COB,
∴∠EOD=∠COA+∠COB=∠AOB=90°,∴OD⊥OE.
(2)证明:∵∠AOD=30°,∴∠COD=30°,
∴∠COE=90°-30°=60°,∠COA=60°,
∴∠COE=∠COA,∴OC为∠AOE的平分线.
(2)若∠AOD=30°,求证:OC为∠AOE的平分线;
(3)若∠AOD∶∠AOE=2∶11,则∠BOE的度数为
.
★10.如图,O为直线AB上一点,OC为射线,OD,OE分别为∠AOC,∠BOC的平分线.
(1)判断射线OD,OE的位置关系,说明理由;
70°
垂线(1)
第五章 相交线与平行线
01
学习目标
02
知识要点
03
对点训练
04
精典范例
05
变式练习
1.(2022新课标)理解垂线的概念,能用三角板或量角器过一点画已知直线的垂线.
2.(2022新课标)掌握基本事实:同一平面内,过一点有且只有一条直线与已知直线垂直.
几何直观 空间观念
推理能力 应用意识
知识点一:垂线
(1)定义:
直线AB与CD相交于点O,若∠AOD=90°,则这两条直线互相 ,记作AB⊥CD(或CD⊥AB),点O叫做垂足.
(2)图示:
垂直
(3)几何语言:
∵∠AOD=90°,∴AB CD.
(4)垂直是相交的一种特殊情形.
(5)画垂线.
⊥
结论:在同一平面内,过一点 一条直线与已知直线垂直.
(3)
有且只有
(2)
1.(人教7下P5、北师7下P41)如图,分别过点P作AB的垂线,垂足为C.
(1)
图略
(3)几何语言:
∵AB⊥CD,
∴∠AOC=∠AOD=∠BOD=∠BOC= °.
知识点二:垂线的性质
(1)垂线的性质:
两直线垂直,则它们的夹角为 °.
(2)图示:
90
90
2.(1)如图,OA⊥OB,∠1=35°,求∠2的度数;
解:(1)∵OA⊥OB,∴∠AOB=90°,
∵∠1=35°,∴∠2=∠AOB-∠1=90°-35°=55°.
(2)如图,OA⊥OB,∠BOC=130°,求∠1的度数.
解:(2)∵OA⊥OB,∴∠AOB=90°,
∵∠BOC=130°,∴∠1=∠BOC-∠AOB=130°-90°=40°.
3.【例1】(人教7下P8)如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,求∠AOD的度数.
解:∵EO⊥AB,
∴∠BOE=90°,
∵∠EOC=35°,
∴∠BOC=∠BOE+∠EOC=125°.
∴∠AOD=∠BOC=125°.
7.(2022河南)如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,求∠2的度数.
解:∵EO⊥CD,∴∠COE=90°,
∵∠1+∠COE+∠2=180°,
∴∠2=180°-∠1-∠COE=180°-54°-90°=36°.
4.【例2】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,求∠CON的度数.
解:∵OM平分∠AOC,∠AOM=35°,
∴∠COM=∠AOM=35°,
∵ON⊥OM,∴∠MON=90°.
∴∠CON=∠MON-∠MOC=90°-35°=55°.
8.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,∠BOD=35°,求∠CON的度数.
解:∵∠BOD=35°,∴∠AOC=∠BOD=35°,
∵OM平分∠AOC,
∴∠COM=∠AOC=17.5°.
∵ON⊥OM,∴∠MON=90°,
∴∠CON=∠MON-∠COM=90°-17.5°=72.5°.
5.【例3】如图,分别过点A,B画OB,OA的垂线.
图略
9.如图,已知∠AOB和OA上一点P.
(1)过点P画PC⊥OA,交OB于点C;
(2)过点P画PD⊥OB,垂足是点D.
图略
6.【例4】如图,O为直线AB上一点,且∠BOC=3∠AOC,OC平分∠AOD.
(1)求∠AOC的度数;
(2)判断OD与AB的位置关系,并说明理由.
解:(1)∵∠BOC=3∠AOC,∠AOC+∠BOC=180°,
∴∠AOC+3∠AOC=180°,解得∠AOC=45°.
(2)OD⊥AB.理由如下:∵OC平分∠AOD,
∴∠AOD=2∠AOC=2×45°=90°,∴OD⊥AB.
(2)若∠AOD=30°,求证:OC为∠AOE的平分线;
(3)若∠AOD∶∠AOE=2∶11,则∠BOE的度数为
.
★10.如图,O为直线AB上一点,OC为射线,OD,OE分别为∠AOC,∠BOC的平分线.
(1)判断射线OD,OE的位置关系,说明理由;
(1)解:垂直,理由如下:
∵OD,OE分别为∠AOC,∠BOC的平分线,
∴∠COD=∠COA,∠COE=∠COB,
∴∠EOD=∠COA+∠COB=∠AOB=90°,∴OD⊥OE.
(2)证明:∵∠AOD=30°,∴∠COD=30°,
∴∠COE=90°-30°=60°,∠COA=60°,
∴∠COE=∠COA,∴OC为∠AOE的平分线.
(2)若∠AOD=30°,求证:OC为∠AOE的平分线;
(3)若∠AOD∶∠AOE=2∶11,则∠BOE的度数为
.
★10.如图,O为直线AB上一点,OC为射线,OD,OE分别为∠AOC,∠BOC的平分线.
(1)判断射线OD,OE的位置关系,说明理由;
70°
