【核心素养目标】2.2不等式的基本性质 教学设计
文档属性
| 名称 | 【核心素养目标】2.2不等式的基本性质 教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 827.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
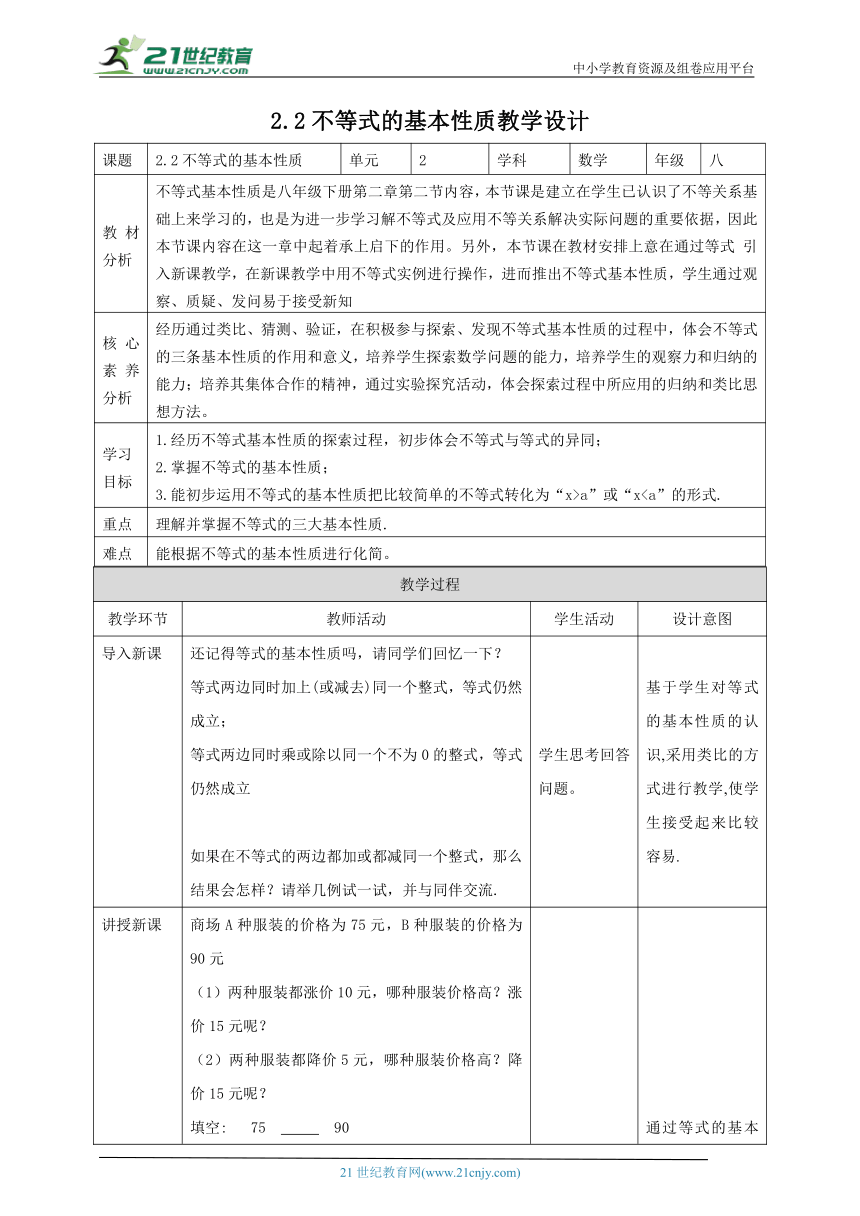
2.2不等式的基本性质教学设计
课题 2.2不等式的基本性质 单元 2 学科 数学 年级 八
教材分析 不等式基本性质是八年级下册第二章第二节内容,本节课是建立在学生已认识了不等关系基础上来学习的,也是为进一步学习解不等式及应用不等关系解决实际问题的重要依据,因此本节课内容在这一章中起着承上启下的作用。另外,本节课在教材安排上意在通过等式 引入新课教学,在新课教学中用不等式实例进行操作,进而推出不等式基本性质,学生通过观察、质疑、发问易于接受新知
核心素养分析 经历通过类比、猜测、验证,在积极参与探索、发现不等式基本性质的过程中,体会不等式的三条基本性质的作用和意义,培养学生探索数学问题的能力,培养学生的观察力和归纳的能力;培养其集体合作的精神,通过实验探究活动,体会探索过程中所应用的归纳和类比思想方法。
学习 目标 1.经历不等式基本性质的探索过程,初步体会不等式与等式的异同; 2.掌握不等式的基本性质; 3.能初步运用不等式的基本性质把比较简单的不等式转化为“x>a”或“x重点 理解并掌握不等式的三大基本性质.
难点 能根据不等式的基本性质进行化简。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 还记得等式的基本性质吗,请同学们回忆一下? 等式两边同时加上(或减去)同一个整式,等式仍然成立; 等式两边同时乘或除以同一个不为0的整式,等式仍然成立 如果在不等式的两边都加或都减同一个整式,那么结果会怎样?请举几例试一试,并与同伴交流. 学生思考回答问题。 基于学生对等式的基本性质的认识,采用类比的方式进行教学,使学生接受起来比较容易.
讲授新课 商场A种服装的价格为75元,B种服装的价格为90元 (1)两种服装都涨价10元,哪种服装价格高?涨价15元呢? (2)两种服装都降价5元,哪种服装价格高?降价15元呢? 填空: 75 90 75+10 90+10 75+15 90+15 75 - 5 90 - 5 75-15 90-15 想一想:75+m 90+m 75 - n 90 - n 你发现了什么规律?你能用自己的话表达出来吗? 归纳: 不等式的基本性质1 不等式的两边都加(或减)同一个整式,不等号的方向不变. 用字母表示为: 如果a > b,那么a + c > b + c,a – c > b - c. 如果a < b,那么a + c < b + c,a – c < b - c. 做一做 完成下列填空: 2 < 3; 2 × 5 __________ 3 × 5; 2 × __________3 ×; 2 × (- 1) _______3 × (- 1); 2 × (- 5) _______3 × (- 5); 2 × ( - ) _______3 ×( - ) 你发现了什么?请再举几例试一试, 还有类似的结论吗?与同伴交流. 归纳: 不等式的基本性质2 不等式两边都乘(或除以)同一个正数,不等号的方向不变. 用字母表示: 如果a>b,c>0,那么ac>bc(或). 不等式的基本性质3: 不等式的两边都乘(或除以)同一个负数,不等号的方向改变. 用字母表示: 如果a>b,c<0,那么ac a”或“x < a”的形式: (1)x - 5 > -1; (2)-2x > 3. 解: (1)根据不等式的基本性质 1,两边都加 5,得x > -1 + 5,即x > 4; (2)根据不等式的基本性质 3,两边都除以 -2,得 学生思考,试着回答问题 学生探讨不等式的基本性质2,3 小组讨论,派一名代表回答。 注:学生口答,老师板书,一来可以检查学生的掌握情况 ,二是可以规范学生的解题格式。 通过等式的基本性质类比得到不等式的基本性质,由特殊的数值到用字母代表数,并从中归纳出一般性结论,进一步发展学生的符号感和提出问题、分析问题、解决问题的能力. 以问题的形式引导学生用类比的方法先猜想不等式的基本性质,再通过具体数值验算性质,最后总结、归纳出性质.在整个教学过程中,学生均处于主导地位,教师只是从旁指引. 在讲解例题的过程中,要求学生说出每一步变形的依据,能说出一个不等式为什么可以从一种形式变形为另一种形式,养成步步有据、准确表达的良好学习习惯,并通过这种方式达到熟练掌握不等式的基本性质的目的.
课堂练习 1.若x<y,则下列不等式中不成立的是( ) A.x-1<y-1 B.3x<3y C.< D.-2x<-2y 2.已知a>b,则-4a□-4b,“□”中应填的符号是( ) A.> B.< C.≥ D.= 3.写出下列不等式的变形依据: (1)若x+4>3,则x>-1,依据: . (2)若>-2,则x>-10,依据: . (3)若-3x>7,则x<-,依据: . (4)若5x-3>2x,则x>1,依据: ; (5)若-4>x,则x<-5,依据: . 4.将下列不等式化成“x>a”或“x<a”的形式: (1)x-1>2; (2)-x<; (3) x<3.1 5.小明做这样一题:已知2x>3x,求x的范围。结果小明两边同时除以x,得到2>3。你知道他错在哪 学生定时训练,自主解答,老师订正 通过练习调动学生学习的积极性,使学生思维处于积极状态,达到了培养学生思维的灵活性和创造性,解决问题的目的。
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 训练学生总结归纳能 力;升华知识,拓展知识面,开阔思维。
板书 课题:2.2 不等式的基本性质 一、不等式的基本性质1 二、不等式的基本性质2 三、不等式的基本性质3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.2不等式的基本性质教学设计
课题 2.2不等式的基本性质 单元 2 学科 数学 年级 八
教材分析 不等式基本性质是八年级下册第二章第二节内容,本节课是建立在学生已认识了不等关系基础上来学习的,也是为进一步学习解不等式及应用不等关系解决实际问题的重要依据,因此本节课内容在这一章中起着承上启下的作用。另外,本节课在教材安排上意在通过等式 引入新课教学,在新课教学中用不等式实例进行操作,进而推出不等式基本性质,学生通过观察、质疑、发问易于接受新知
核心素养分析 经历通过类比、猜测、验证,在积极参与探索、发现不等式基本性质的过程中,体会不等式的三条基本性质的作用和意义,培养学生探索数学问题的能力,培养学生的观察力和归纳的能力;培养其集体合作的精神,通过实验探究活动,体会探索过程中所应用的归纳和类比思想方法。
学习 目标 1.经历不等式基本性质的探索过程,初步体会不等式与等式的异同; 2.掌握不等式的基本性质; 3.能初步运用不等式的基本性质把比较简单的不等式转化为“x>a”或“x
难点 能根据不等式的基本性质进行化简。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 还记得等式的基本性质吗,请同学们回忆一下? 等式两边同时加上(或减去)同一个整式,等式仍然成立; 等式两边同时乘或除以同一个不为0的整式,等式仍然成立 如果在不等式的两边都加或都减同一个整式,那么结果会怎样?请举几例试一试,并与同伴交流. 学生思考回答问题。 基于学生对等式的基本性质的认识,采用类比的方式进行教学,使学生接受起来比较容易.
讲授新课 商场A种服装的价格为75元,B种服装的价格为90元 (1)两种服装都涨价10元,哪种服装价格高?涨价15元呢? (2)两种服装都降价5元,哪种服装价格高?降价15元呢? 填空: 75 90 75+10 90+10 75+15 90+15 75 - 5 90 - 5 75-15 90-15 想一想:75+m 90+m 75 - n 90 - n 你发现了什么规律?你能用自己的话表达出来吗? 归纳: 不等式的基本性质1 不等式的两边都加(或减)同一个整式,不等号的方向不变. 用字母表示为: 如果a > b,那么a + c > b + c,a – c > b - c. 如果a < b,那么a + c < b + c,a – c < b - c. 做一做 完成下列填空: 2 < 3; 2 × 5 __________ 3 × 5; 2 × __________3 ×; 2 × (- 1) _______3 × (- 1); 2 × (- 5) _______3 × (- 5); 2 × ( - ) _______3 ×( - ) 你发现了什么?请再举几例试一试, 还有类似的结论吗?与同伴交流. 归纳: 不等式的基本性质2 不等式两边都乘(或除以)同一个正数,不等号的方向不变. 用字母表示: 如果a>b,c>0,那么ac>bc(或). 不等式的基本性质3: 不等式的两边都乘(或除以)同一个负数,不等号的方向改变. 用字母表示: 如果a>b,c<0,那么ac
课堂练习 1.若x<y,则下列不等式中不成立的是( ) A.x-1<y-1 B.3x<3y C.< D.-2x<-2y 2.已知a>b,则-4a□-4b,“□”中应填的符号是( ) A.> B.< C.≥ D.= 3.写出下列不等式的变形依据: (1)若x+4>3,则x>-1,依据: . (2)若>-2,则x>-10,依据: . (3)若-3x>7,则x<-,依据: . (4)若5x-3>2x,则x>1,依据: ; (5)若-4>x,则x<-5,依据: . 4.将下列不等式化成“x>a”或“x<a”的形式: (1)x-1>2; (2)-x<; (3) x<3.1 5.小明做这样一题:已知2x>3x,求x的范围。结果小明两边同时除以x,得到2>3。你知道他错在哪 学生定时训练,自主解答,老师订正 通过练习调动学生学习的积极性,使学生思维处于积极状态,达到了培养学生思维的灵活性和创造性,解决问题的目的。
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 训练学生总结归纳能 力;升华知识,拓展知识面,开阔思维。
板书 课题:2.2 不等式的基本性质 一、不等式的基本性质1 二、不等式的基本性质2 三、不等式的基本性质3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
