广东省汕头市龙湖实验中学2022-2023学年九年级下学期开学考试数学试题(含答案)
文档属性
| 名称 | 广东省汕头市龙湖实验中学2022-2023学年九年级下学期开学考试数学试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-10 00:00:00 | ||
图片预览


文档简介
汕头市龙湖实验中学2022-2023学年度下学期开学测评卷
初三数学
一、选择题(本大题10小题,每小题3分,共30分)
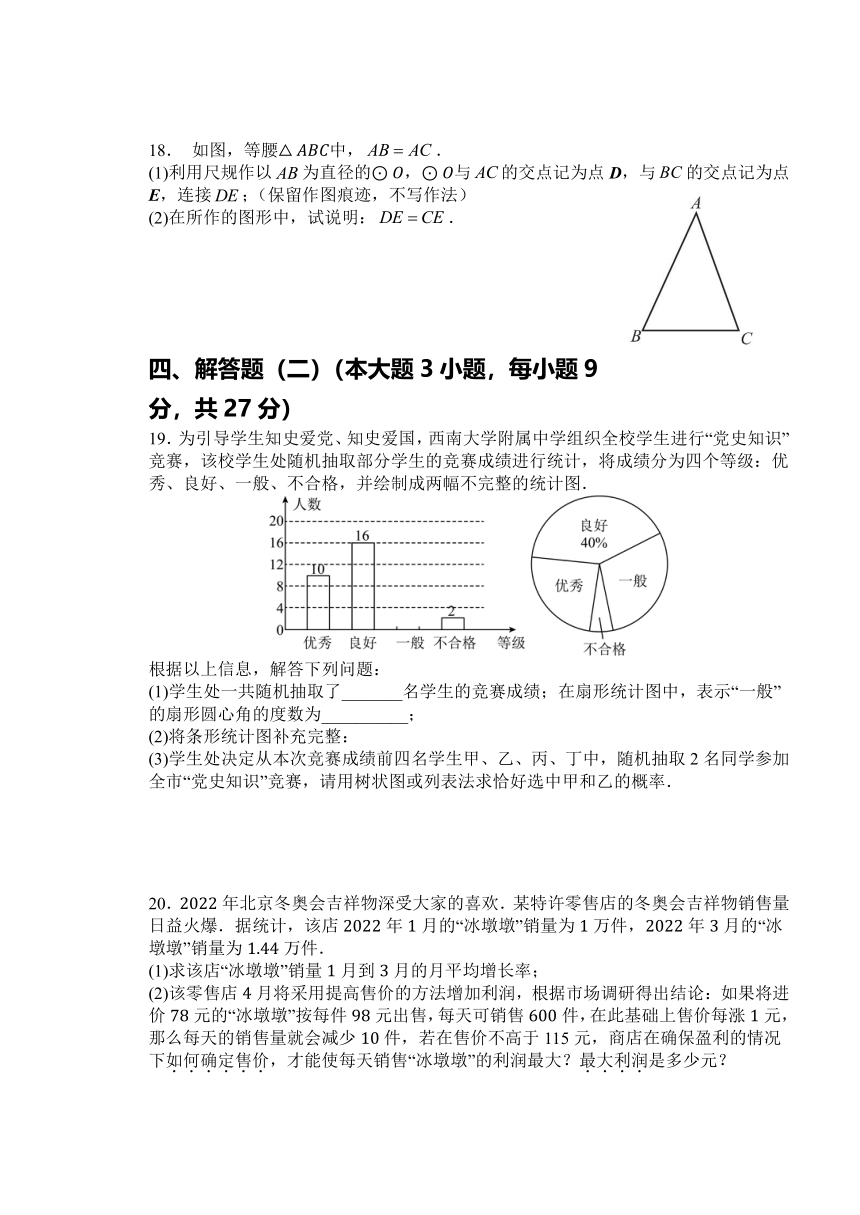
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.如果是一元二次方程的解,那么的值是( )
A.0 B.2 C.6 D.
3.卡塔尔世界杯足球赛中,“运动员梅西射门一次,成功进球得分”这事件是( )
A.确定事件 B.必然事件 C.不可能事件 D.随机事件
4.已知函数的图像如图所示,则下列结论正确的是( )
A. B.
C. D.
第4题 第5题 第6题
5.如图,在中,,,分别是边,,上的点,,,且,那么的值为( )
A. B. C. D.
6.如图,将绕点A逆时针旋转得,若点在线段的延长线上,则的度数为( )
A. B. C. D.
7.如图,点P是反比例函数图像上的一点,轴于F点,且面积为4.若点也是该图像上的一点,则m的值为( )
A.-2 B.-4 C.2 D.4
8.如图,点、、、为一个正多边形的顶点,点为正多边形的中心,若,则这个正多边形的边数为( )
A.5 B.10 C.12 D.20
第7题 第8题 第9题
9.如图,菱形的边长为2,,以为圆心的弧与边、相切,则阴影部分的面积为( )
A. B. C. D.
10.如图,已知,在正方形中,,以点B为圆心,1为半径作,点P在上移动,连接.将绕点A逆时针旋转至,连接.在点P移动过程中,长度的最小值是( )
A. B. C. D.3
二、填空题(本大题5小题,每小题3分,共15分)
11.平面直角坐标系中,一点关于原点的对称点的坐标是_________.
12.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果水的最大深度为,水面宽为,则输水管的半径为______.
第12题 第13题 第15题
13.在平行四边形中,点E是边上一点,且,交对角线于点F,则与的面积比值为_____________.
14.已知二次函数的图象上有两点,,则___________(填“>”“<”或“=”)
15.如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An 1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y= (x>0)的图象于点B1,B2,B3,…,Bn,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn,则S1+S2+S3+…+Sn=______________.
三、解答题(一)(本大题3小题,每小题8分,共24分)
16.计算:.
17.如图,D为内一点,,,将绕着点A顺时针旋转能与线段重合.
(1)求证:;
(2)若,直接写出的度数:_____________.
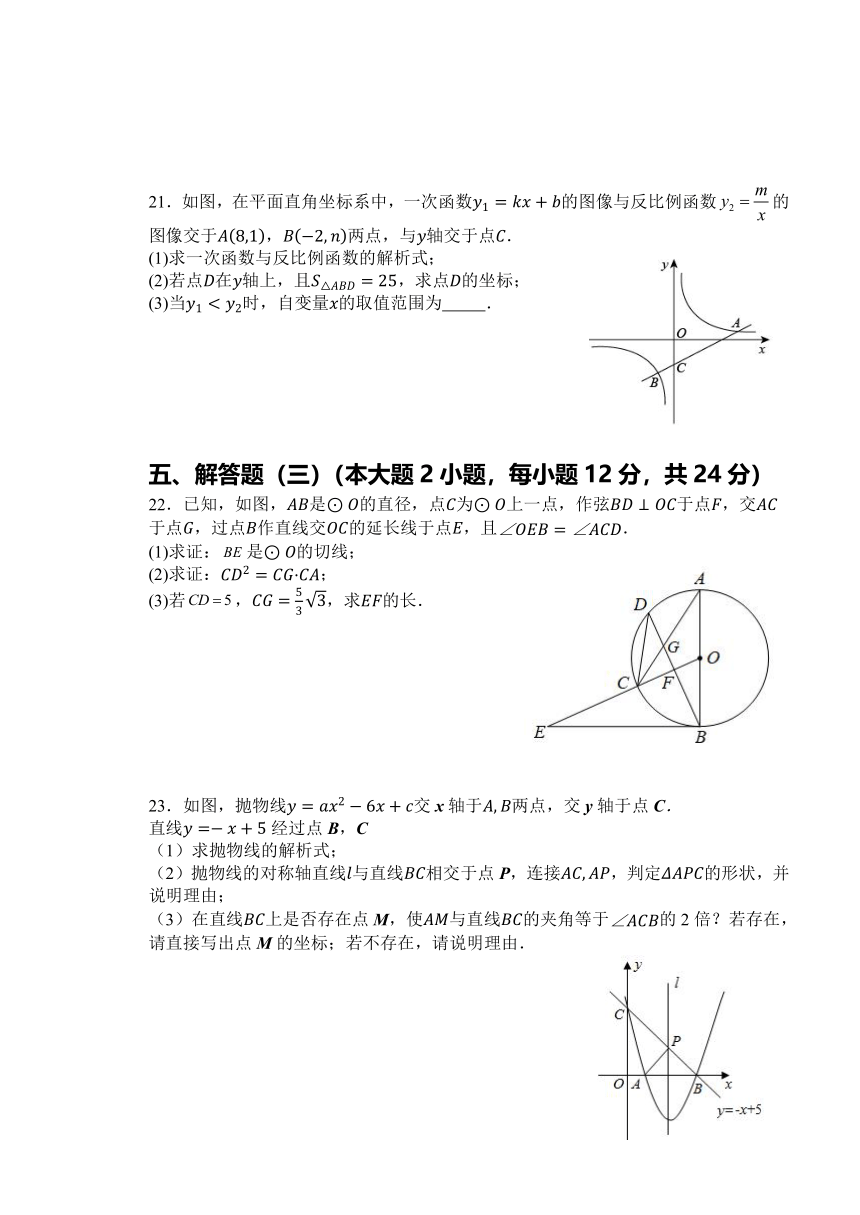
18. 如图,等腰中,.
(1)利用尺规作以为直径的,与的交点记为点D,与的交点记为点E,连接;(保留作图痕迹,不写作法)
(2)在所作的图形中,试说明:.
四、解答题(二)(本大题3小题,每小题9分,共27分)
19.为引导学生知史爱党、知史爱国,西南大学附属中学组织全校学生进行“党史知识”竞赛,该校学生处随机抽取部分学生的竞赛成绩进行统计,将成绩分为四个等级:优秀、良好、一般、不合格,并绘制成两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)学生处一共随机抽取了_______名学生的竞赛成绩;在扇形统计图中,表示“一般”的扇形圆心角的度数为__________;
(2)将条形统计图补充完整:
(3)学生处决定从本次竞赛成绩前四名学生甲、乙、丙、丁中,随机抽取2名同学参加全市“党史知识”竞赛,请用树状图或列表法求恰好选中甲和乙的概率.
20.年北京冬奥会吉祥物深受大家的喜欢.某特许零售店的冬奥会吉祥物销售量日益火爆.据统计,该店年月的“冰墩墩”销量为万件,年月的“冰墩墩”销量为万件.
(1)求该店“冰墩墩”销量月到月的月平均增长率;
(2)该零售店月将采用提高售价的方法增加利润,根据市场调研得出结论:如果将进价元的“冰墩墩”按每件元出售,每天可销售件,在此基础上售价每涨元,那么每天的销售量就会减少件,若在售价不高于115元,商店在确保盈利的情况下如何确定售价,才能使每天销售“冰墩墩”的利润最大?最大利润是多少元?
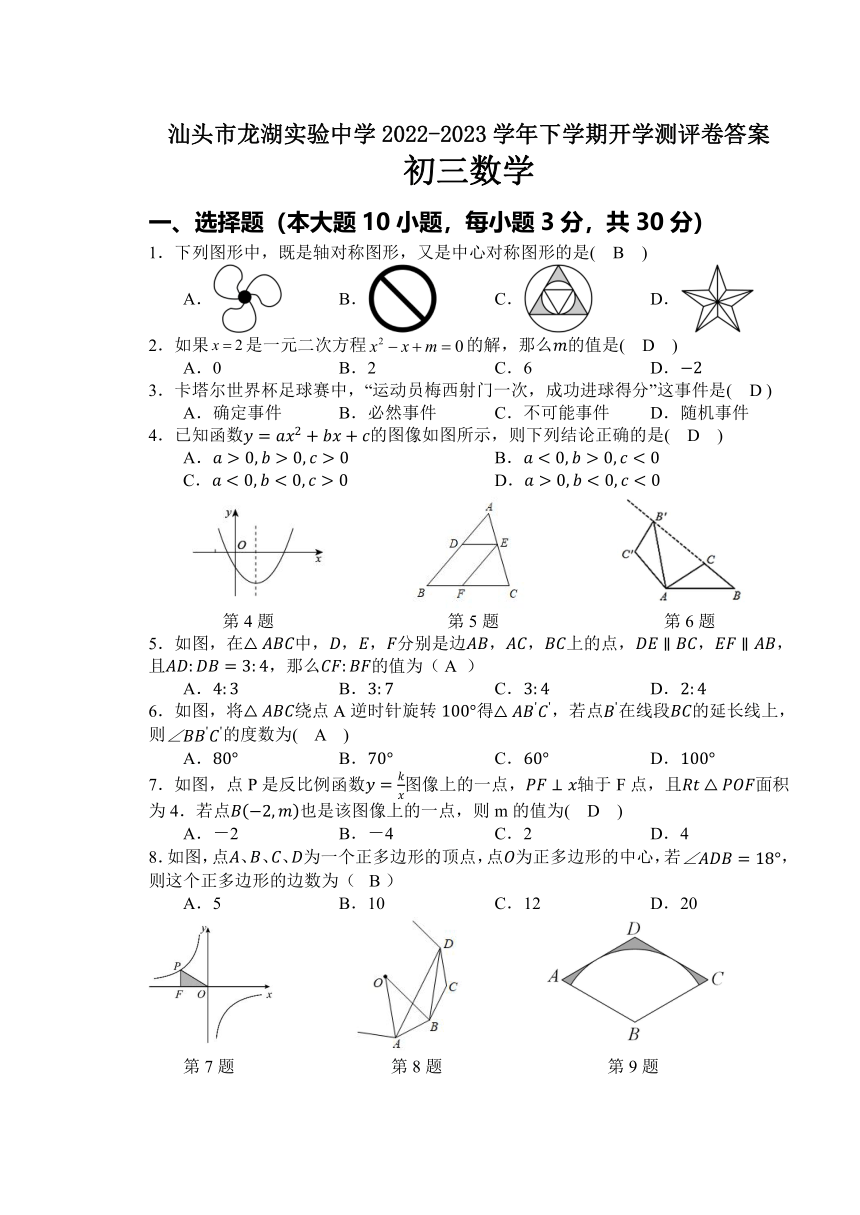
21.如图,在平面直角坐标系中,一次函数的图像与反比例函数的图像交于,两点,与轴交于点.
(1)求一次函数与反比例函数的解析式;
(2)若点在轴上,且,求点的坐标;
(3)当时,自变量的取值范围为 .
五、解答题(三)(本大题2小题,每小题12分,共24分)
22.已知,如图,是的直径,点为上一点,作弦于点,交于点,过点作直线交的延长线于点,且.
(1)求证:是的切线;
(2)求证:;
(3)若,,求的长.
23.如图,抛物线交x轴于两点,交y轴于点C.
直线经过点B,C
(1)求抛物线的解析式;
(2)抛物线的对称轴直线与直线相交于点P,连接,判定的形状,并说明理由;
(3)在直线上是否存在点M,使与直线的夹角等于的2倍?若存在,请直接写出点M的坐标;若不存在,请说明理由.
汕头市龙湖实验中学2022-2023学年下学期开学测评卷答案
初三数学
一、选择题(本大题10小题,每小题3分,共30分)
1.下列图形中,既是轴对称图形,又是中心对称图形的是( B )
A. B. C. D.
2.如果是一元二次方程的解,那么的值是( D )
A.0 B.2 C.6 D.
3.卡塔尔世界杯足球赛中,“运动员梅西射门一次,成功进球得分”这事件是( D )
A.确定事件 B.必然事件 C.不可能事件 D.随机事件
4.已知函数的图像如图所示,则下列结论正确的是( D )
A. B.
C. D.
第4题 第5题 第6题
5.如图,在中,,,分别是边,,上的点,,,且,那么的值为( A )
A. B. C. D.
6.如图,将绕点A逆时针旋转得,若点在线段的延长线上,则的度数为( A )
A. B. C. D.
7.如图,点P是反比例函数图像上的一点,轴于F点,且面积为4.若点也是该图像上的一点,则m的值为( D )
A.-2 B.-4 C.2 D.4
8.如图,点、、、为一个正多边形的顶点,点为正多边形的中心,若,则这个正多边形的边数为( B )
A.5 B.10 C.12 D.20
第7题 第8题 第9题
9.如图,菱形的边长为2,,以为圆心的弧与边、相切,则阴影部分的面积为( B )
A. B. C. D.
10.如图,已知,在正方形中,,以点B为圆心,1为半径作,点P在上移动,连接.将绕点A逆时针旋转至,连接.在点P移动过程中,长度的最小值是( A )
A. B. C. D.3
二、填空题(本大题5小题,每小题3分,共15分)
11.平面直角坐标系中,一点关于原点的对称点的坐标是_____.
12.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果水的最大深度为,水面宽为,则输水管的半径为___10___.
第12题 第13题 第15题
13.在平行四边形中,点E是边上一点,且,交对角线于点F,则与的面积比值为________9_____.
14.已知二次函数的图象上有两点,,则______<_____(填“>”“<”或“=”)
15.如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An 1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y= (x>0)的图象于点B1,B2,B3,…,Bn,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn,则S1+S2+S3+…+Sn=______________.
三、解答题(一)(本大题3小题,每小题8分,共24分)
16.计算:.
解:原式
17.如图,D为内一点,,,将绕着点A顺时针旋转能与线段重合.
(1)求证:;
(2)若,直接写出的度数:___30°___.
解:(1)证明:由旋转的性质可得:,,
∵,
∴,
∴,
在和中,
,
∴,
∴;
18. 如图,等腰中,.
(1)利用尺规作以为直径的,与的交点记为点D,与的交点记为点E,连接;(保留作图痕迹,不写作法)
(2)在所作的图形中,试说明:.
(1)解:如图, 即为所求作.
(2)证明:,
,
∵四边形为的内接四边形,
,
又,
,
,
.
四、解答题(二)(本大题3小题,每小题9分,共27分)
19.为引导学生知史爱党、知史爱国,西南大学附属中学组织全校学生进行“党史知识”竞赛,该校学生处随机抽取部分学生的竞赛成绩进行统计,将成绩分为四个等级:优秀、良好、一般、不合格,并绘制成两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)学生处一共随机抽取了____40___名学生的竞赛成绩;在扇形统计图中,表示“一般”的扇形圆心角的度数为_____108°_____;
(2)将条形统计图补充完整:
(3)学生处决定从本次竞赛成绩前四名学生甲、乙、丙、丁中,随机抽取2名同学参加全市“党史知识”竞赛,请用树状图或列表法求恰好选中甲和乙的概率.
解:(2)把条形统计图补充完整如下;
(3)画树状图如图:
共有12种等可能的结果,恰好选中甲和乙的结果有2种,
∴恰好选中甲和乙的概率为.
20.年北京冬奥会吉祥物深受大家的喜欢.某特许零售店的冬奥会吉祥物销售量日益火爆.据统计,该店年月的“冰墩墩”销量为万件,年月的“冰墩墩”销量为万件.
(1)求该店“冰墩墩”销量月到月的月平均增长率;
(2)该零售店月将采用提高售价的方法增加利润,根据市场调研得出结论:如果将进价元的“冰墩墩”按每件元出售,每天可销售件,在此基础上售价每涨元,那么每天的销售量就会减少件,若在售价不高于115元,商店在确保盈利的情况下如何确定售价,才能使每天销售“冰墩墩”的利润最大?最大利润是多少元?
解:(1)设该店“冰墩墩”销量的月平均增长率为,
由题意可得,,
解得,舍去,
答:该店“冰墩墩”销量的月平均增长率为
(2)设每件商品的涨价元,利润为元,
则每件商品的销售利润为元,每天的销售量为件,
依题意可得
,
由 得,
抛物线开口向下
当,利润最大元,
既当售价为元时,利润最大为元
21.如图,在平面直角坐标系中,一次函数的图像与反比例函数的图像交于,两点,与轴交于点.
(1)求一次函数与反比例函数的解析式;
(2)若点在轴上,且,求点的坐标;
(3)当时,自变量的取值范围为 或 .
(1)∵点在比例函数上,
∴,
∴,
∴;
∵点在反比例函数上,
∴,
∴,
∴点,
∵点,点经过一次函数,
∴,
解得:,
∴.
∴一次函数的解析式为:,反比例函数的解析式为:.
(2)如图,所示:
设点,
∵点在一次函数且与轴相交,
∴点,
∴,
∴,
∴,
∴,
∴,
∴,,
∴点或.
五、解答题(三)(本大题2小题,每小题12分,共24分)
22.已知,如图,是的直径,点为上一点,作弦于点,交于点,过点作直线交的延长线于点,且.
(1)求证:是的切线;
(2)求证:;
(3)若,,求的长.
(1)证明:,
,
,
.
,
,
即,
是的半径,
是的切线;
(2)证明:连接,如图,
是的半径,,
,
,
,
,
.
;
(3)解:连接,如图,
由(2)知:,
,,
.
,
,
.
是的直径,
.
,
.
.
,
.
,
.
,,
.
23.如图,抛物线交x轴于两点,交y轴于点C.
直线经过点B,C
(1)求抛物线的解析式;
(2)抛物线的对称轴直线与直线相交于点P,连接,判定的形状,并说明理由;
(3)在直线上是否存在点M,使与直线的夹角等于的2倍?若存在,请直接写出点M的坐标;若不存在,请说明理由.
解:(1将C(0,5)B(5,0)代入
∴
解得
∴该抛物线的解析式为
(2)的为直角三角形,理由如下:
∵解方程=0,
则x1=1,x2=5
∴A(1,0),B(5,0)
∵抛物线的对称轴为直线x=3
∴△APB为等腰三角形
∵C的坐标为(5,0),B的坐标为(5,0)
∴OB=CO=5,即∠ABP=45°
∴∠ABP=45°,
∴∠APB=180°-45°-45°=90°
∴∠APC=180°-90°=90°
∴的为直角三角形;
(3)如图:作AN⊥BC于N,NH⊥x轴于H,作AC的垂直平分线交BC于,AC于E,
∵M1A=M1C,
∴∠ACM1=∠CAM1
∴∠AM1B=2∠ACB
∵△ANB为等腰直角三角形.
∴AH=BH=NH=2
∴N(3,2)
设AC的函数解析式为y=kx+b
∵C(0,5),A(1,0)
∴解得b=5,k=-5
∴AC的函数解析式为y=-5x+5
设EM1的函数解析式为y=x+n
∵点E的坐标为()
∴=×+n,解得:n=
∴EM1的函数解析式为y=x+
∵解得
∴M1的坐标为();
在直线BC上作点M1关于N点的对称点M2
设M2(a,-a+5)
则有:3=,解得a=
∴-a+5=
∴M2的坐标为(,).
综上,M1(),M2(,).
初三数学
一、选择题(本大题10小题,每小题3分,共30分)
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.如果是一元二次方程的解,那么的值是( )
A.0 B.2 C.6 D.
3.卡塔尔世界杯足球赛中,“运动员梅西射门一次,成功进球得分”这事件是( )
A.确定事件 B.必然事件 C.不可能事件 D.随机事件
4.已知函数的图像如图所示,则下列结论正确的是( )
A. B.
C. D.
第4题 第5题 第6题
5.如图,在中,,,分别是边,,上的点,,,且,那么的值为( )
A. B. C. D.
6.如图,将绕点A逆时针旋转得,若点在线段的延长线上,则的度数为( )
A. B. C. D.
7.如图,点P是反比例函数图像上的一点,轴于F点,且面积为4.若点也是该图像上的一点,则m的值为( )
A.-2 B.-4 C.2 D.4
8.如图,点、、、为一个正多边形的顶点,点为正多边形的中心,若,则这个正多边形的边数为( )
A.5 B.10 C.12 D.20
第7题 第8题 第9题
9.如图,菱形的边长为2,,以为圆心的弧与边、相切,则阴影部分的面积为( )
A. B. C. D.
10.如图,已知,在正方形中,,以点B为圆心,1为半径作,点P在上移动,连接.将绕点A逆时针旋转至,连接.在点P移动过程中,长度的最小值是( )
A. B. C. D.3
二、填空题(本大题5小题,每小题3分,共15分)
11.平面直角坐标系中,一点关于原点的对称点的坐标是_________.
12.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果水的最大深度为,水面宽为,则输水管的半径为______.
第12题 第13题 第15题
13.在平行四边形中,点E是边上一点,且,交对角线于点F,则与的面积比值为_____________.
14.已知二次函数的图象上有两点,,则___________(填“>”“<”或“=”)
15.如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An 1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y= (x>0)的图象于点B1,B2,B3,…,Bn,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn,则S1+S2+S3+…+Sn=______________.
三、解答题(一)(本大题3小题,每小题8分,共24分)
16.计算:.
17.如图,D为内一点,,,将绕着点A顺时针旋转能与线段重合.
(1)求证:;
(2)若,直接写出的度数:_____________.
18. 如图,等腰中,.
(1)利用尺规作以为直径的,与的交点记为点D,与的交点记为点E,连接;(保留作图痕迹,不写作法)
(2)在所作的图形中,试说明:.
四、解答题(二)(本大题3小题,每小题9分,共27分)
19.为引导学生知史爱党、知史爱国,西南大学附属中学组织全校学生进行“党史知识”竞赛,该校学生处随机抽取部分学生的竞赛成绩进行统计,将成绩分为四个等级:优秀、良好、一般、不合格,并绘制成两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)学生处一共随机抽取了_______名学生的竞赛成绩;在扇形统计图中,表示“一般”的扇形圆心角的度数为__________;
(2)将条形统计图补充完整:
(3)学生处决定从本次竞赛成绩前四名学生甲、乙、丙、丁中,随机抽取2名同学参加全市“党史知识”竞赛,请用树状图或列表法求恰好选中甲和乙的概率.
20.年北京冬奥会吉祥物深受大家的喜欢.某特许零售店的冬奥会吉祥物销售量日益火爆.据统计,该店年月的“冰墩墩”销量为万件,年月的“冰墩墩”销量为万件.
(1)求该店“冰墩墩”销量月到月的月平均增长率;
(2)该零售店月将采用提高售价的方法增加利润,根据市场调研得出结论:如果将进价元的“冰墩墩”按每件元出售,每天可销售件,在此基础上售价每涨元,那么每天的销售量就会减少件,若在售价不高于115元,商店在确保盈利的情况下如何确定售价,才能使每天销售“冰墩墩”的利润最大?最大利润是多少元?
21.如图,在平面直角坐标系中,一次函数的图像与反比例函数的图像交于,两点,与轴交于点.
(1)求一次函数与反比例函数的解析式;
(2)若点在轴上,且,求点的坐标;
(3)当时,自变量的取值范围为 .
五、解答题(三)(本大题2小题,每小题12分,共24分)
22.已知,如图,是的直径,点为上一点,作弦于点,交于点,过点作直线交的延长线于点,且.
(1)求证:是的切线;
(2)求证:;
(3)若,,求的长.
23.如图,抛物线交x轴于两点,交y轴于点C.
直线经过点B,C
(1)求抛物线的解析式;
(2)抛物线的对称轴直线与直线相交于点P,连接,判定的形状,并说明理由;
(3)在直线上是否存在点M,使与直线的夹角等于的2倍?若存在,请直接写出点M的坐标;若不存在,请说明理由.
汕头市龙湖实验中学2022-2023学年下学期开学测评卷答案
初三数学
一、选择题(本大题10小题,每小题3分,共30分)
1.下列图形中,既是轴对称图形,又是中心对称图形的是( B )
A. B. C. D.
2.如果是一元二次方程的解,那么的值是( D )
A.0 B.2 C.6 D.
3.卡塔尔世界杯足球赛中,“运动员梅西射门一次,成功进球得分”这事件是( D )
A.确定事件 B.必然事件 C.不可能事件 D.随机事件
4.已知函数的图像如图所示,则下列结论正确的是( D )
A. B.
C. D.
第4题 第5题 第6题
5.如图,在中,,,分别是边,,上的点,,,且,那么的值为( A )
A. B. C. D.
6.如图,将绕点A逆时针旋转得,若点在线段的延长线上,则的度数为( A )
A. B. C. D.
7.如图,点P是反比例函数图像上的一点,轴于F点,且面积为4.若点也是该图像上的一点,则m的值为( D )
A.-2 B.-4 C.2 D.4
8.如图,点、、、为一个正多边形的顶点,点为正多边形的中心,若,则这个正多边形的边数为( B )
A.5 B.10 C.12 D.20
第7题 第8题 第9题
9.如图,菱形的边长为2,,以为圆心的弧与边、相切,则阴影部分的面积为( B )
A. B. C. D.
10.如图,已知,在正方形中,,以点B为圆心,1为半径作,点P在上移动,连接.将绕点A逆时针旋转至,连接.在点P移动过程中,长度的最小值是( A )
A. B. C. D.3
二、填空题(本大题5小题,每小题3分,共15分)
11.平面直角坐标系中,一点关于原点的对称点的坐标是_____.
12.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果水的最大深度为,水面宽为,则输水管的半径为___10___.
第12题 第13题 第15题
13.在平行四边形中,点E是边上一点,且,交对角线于点F,则与的面积比值为________9_____.
14.已知二次函数的图象上有两点,,则______<_____(填“>”“<”或“=”)
15.如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An 1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y= (x>0)的图象于点B1,B2,B3,…,Bn,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn,则S1+S2+S3+…+Sn=______________.
三、解答题(一)(本大题3小题,每小题8分,共24分)
16.计算:.
解:原式
17.如图,D为内一点,,,将绕着点A顺时针旋转能与线段重合.
(1)求证:;
(2)若,直接写出的度数:___30°___.
解:(1)证明:由旋转的性质可得:,,
∵,
∴,
∴,
在和中,
,
∴,
∴;
18. 如图,等腰中,.
(1)利用尺规作以为直径的,与的交点记为点D,与的交点记为点E,连接;(保留作图痕迹,不写作法)
(2)在所作的图形中,试说明:.
(1)解:如图, 即为所求作.
(2)证明:,
,
∵四边形为的内接四边形,
,
又,
,
,
.
四、解答题(二)(本大题3小题,每小题9分,共27分)
19.为引导学生知史爱党、知史爱国,西南大学附属中学组织全校学生进行“党史知识”竞赛,该校学生处随机抽取部分学生的竞赛成绩进行统计,将成绩分为四个等级:优秀、良好、一般、不合格,并绘制成两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)学生处一共随机抽取了____40___名学生的竞赛成绩;在扇形统计图中,表示“一般”的扇形圆心角的度数为_____108°_____;
(2)将条形统计图补充完整:
(3)学生处决定从本次竞赛成绩前四名学生甲、乙、丙、丁中,随机抽取2名同学参加全市“党史知识”竞赛,请用树状图或列表法求恰好选中甲和乙的概率.
解:(2)把条形统计图补充完整如下;
(3)画树状图如图:
共有12种等可能的结果,恰好选中甲和乙的结果有2种,
∴恰好选中甲和乙的概率为.
20.年北京冬奥会吉祥物深受大家的喜欢.某特许零售店的冬奥会吉祥物销售量日益火爆.据统计,该店年月的“冰墩墩”销量为万件,年月的“冰墩墩”销量为万件.
(1)求该店“冰墩墩”销量月到月的月平均增长率;
(2)该零售店月将采用提高售价的方法增加利润,根据市场调研得出结论:如果将进价元的“冰墩墩”按每件元出售,每天可销售件,在此基础上售价每涨元,那么每天的销售量就会减少件,若在售价不高于115元,商店在确保盈利的情况下如何确定售价,才能使每天销售“冰墩墩”的利润最大?最大利润是多少元?
解:(1)设该店“冰墩墩”销量的月平均增长率为,
由题意可得,,
解得,舍去,
答:该店“冰墩墩”销量的月平均增长率为
(2)设每件商品的涨价元,利润为元,
则每件商品的销售利润为元,每天的销售量为件,
依题意可得
,
由 得,
抛物线开口向下
当,利润最大元,
既当售价为元时,利润最大为元
21.如图,在平面直角坐标系中,一次函数的图像与反比例函数的图像交于,两点,与轴交于点.
(1)求一次函数与反比例函数的解析式;
(2)若点在轴上,且,求点的坐标;
(3)当时,自变量的取值范围为 或 .
(1)∵点在比例函数上,
∴,
∴,
∴;
∵点在反比例函数上,
∴,
∴,
∴点,
∵点,点经过一次函数,
∴,
解得:,
∴.
∴一次函数的解析式为:,反比例函数的解析式为:.
(2)如图,所示:
设点,
∵点在一次函数且与轴相交,
∴点,
∴,
∴,
∴,
∴,
∴,
∴,,
∴点或.
五、解答题(三)(本大题2小题,每小题12分,共24分)
22.已知,如图,是的直径,点为上一点,作弦于点,交于点,过点作直线交的延长线于点,且.
(1)求证:是的切线;
(2)求证:;
(3)若,,求的长.
(1)证明:,
,
,
.
,
,
即,
是的半径,
是的切线;
(2)证明:连接,如图,
是的半径,,
,
,
,
,
.
;
(3)解:连接,如图,
由(2)知:,
,,
.
,
,
.
是的直径,
.
,
.
.
,
.
,
.
,,
.
23.如图,抛物线交x轴于两点,交y轴于点C.
直线经过点B,C
(1)求抛物线的解析式;
(2)抛物线的对称轴直线与直线相交于点P,连接,判定的形状,并说明理由;
(3)在直线上是否存在点M,使与直线的夹角等于的2倍?若存在,请直接写出点M的坐标;若不存在,请说明理由.
解:(1将C(0,5)B(5,0)代入
∴
解得
∴该抛物线的解析式为
(2)的为直角三角形,理由如下:
∵解方程=0,
则x1=1,x2=5
∴A(1,0),B(5,0)
∵抛物线的对称轴为直线x=3
∴△APB为等腰三角形
∵C的坐标为(5,0),B的坐标为(5,0)
∴OB=CO=5,即∠ABP=45°
∴∠ABP=45°,
∴∠APB=180°-45°-45°=90°
∴∠APC=180°-90°=90°
∴的为直角三角形;
(3)如图:作AN⊥BC于N,NH⊥x轴于H,作AC的垂直平分线交BC于,AC于E,
∵M1A=M1C,
∴∠ACM1=∠CAM1
∴∠AM1B=2∠ACB
∵△ANB为等腰直角三角形.
∴AH=BH=NH=2
∴N(3,2)
设AC的函数解析式为y=kx+b
∵C(0,5),A(1,0)
∴解得b=5,k=-5
∴AC的函数解析式为y=-5x+5
设EM1的函数解析式为y=x+n
∵点E的坐标为()
∴=×+n,解得:n=
∴EM1的函数解析式为y=x+
∵解得
∴M1的坐标为();
在直线BC上作点M1关于N点的对称点M2
设M2(a,-a+5)
则有:3=,解得a=
∴-a+5=
∴M2的坐标为(,).
综上,M1(),M2(,).
同课章节目录
