广东省汕头市龙湖实验中学2022-2023学年八年级下学期开学考试数学试题(含答案)
文档属性
| 名称 | 广东省汕头市龙湖实验中学2022-2023学年八年级下学期开学考试数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 639.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-10 00:00:00 | ||
图片预览


文档简介
汕头市龙湖实验中学2022-2023学年下学期开学测评卷
初二数学
一.选择题(本题共10小题,每小题3分,共30分)
1.2022年卡塔尔世界杯举办的第22届世界杯,历届世界杯可谓各具特色,会徽设计也蕴含了不同的文化.下列世界杯会徽的图案中,属于轴对称图形的是
A. B. C. D.
2.作为“广元七绝”之一绝的青川黑木耳因其朵大质厚、色泽深邃、细质滑美的特点被人们喜爱.黑木耳属于菌类,已知某种真菌的直径为,将该数据用科学记数法可以表示为
A. B. C. D.
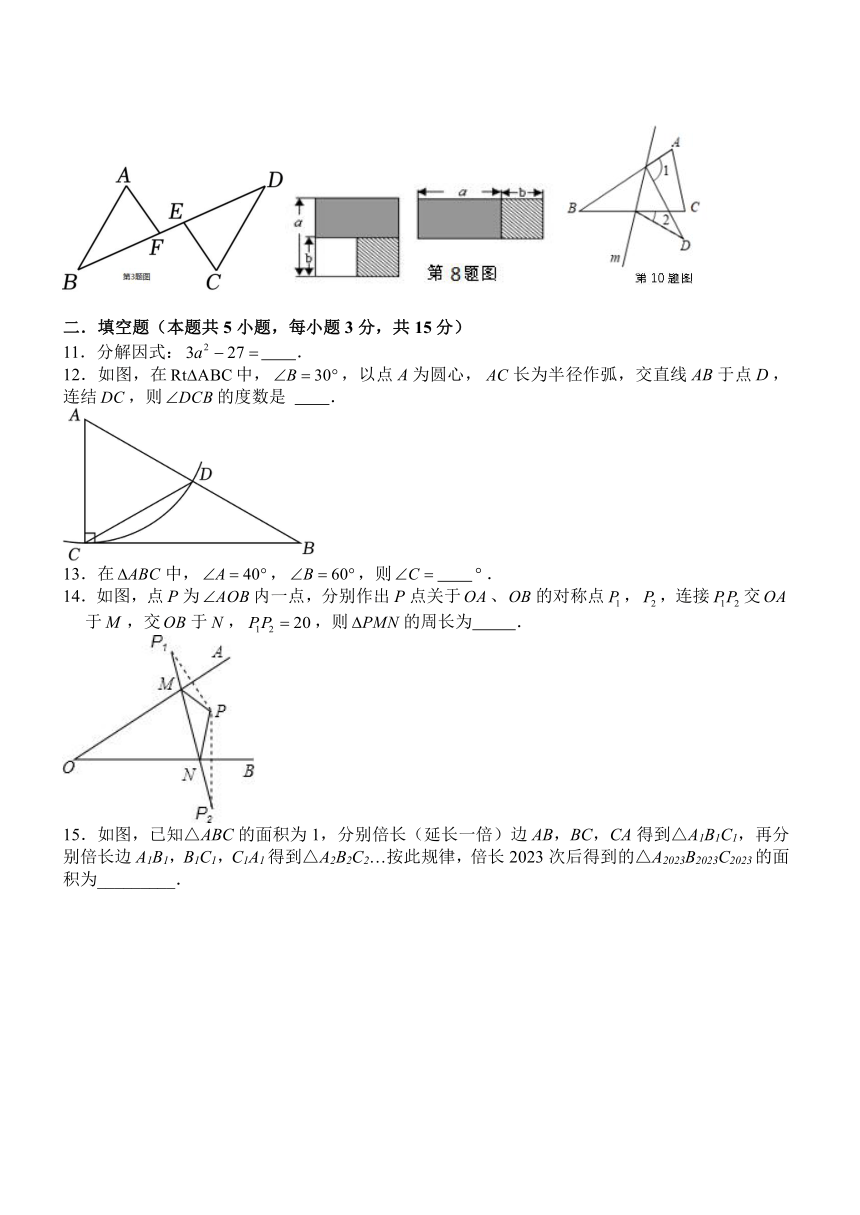
3.如图,已知,,要使,添加的条件可以是
A. B. C. D.
4.已知等腰三角形的一个角为,则该三角形的顶角为
A. B. C.或 D.以上都不对
5.分式的值为零,则的值为
A. B.2 C. D.0或2
6.在平面直角坐标系中,点关于轴的对称点的坐标是
. . . .
7.下列长度的三条线段首尾相接不能围成三角形的是
A.2,3,4 B.8,7,15 C.6,8,10 D.13,12,20
8.从边长为的正方形中去掉一个边长为的小正方形,如图,然后将剩余部分剪后拼成一个矩形,上述操作所能验证的等式是( )
A. B.
C. D.
9.已知满足,则的值为( )
A.1 B.-5 C.-3 D.-7
10.如图,在△ABC中,∠B=32°,将△ABC沿直线翻折,点B落在点D的位置,则
的度数是( )
A. B. C. D.
二.填空题(本题共5小题,每小题3分,共15分)
11.分解因式: .
12.如图,在中,,以点为圆心,长为半径作弧,交直线于点,连结,则的度数是 .
13.在中,,,则 .
14.如图,点为内一点,分别作出点关于、的对称点,,连接交于,交于,,则的周长为 .
15.如图,已知△ABC的面积为1,分别倍长(延长一倍)边AB,BC,CA得到△A1B1C1,再分别倍长边A1B1,B1C1,C1A1得到△A2B2C2…按此规律,倍长2023次后得到的△A2023B2023C2023的面积为_________.
三.解答题(一)(本大题共3小题,每小题8分,共24分)
16.计算:.
17.解分式方程:.
18.先化简,再求值:请从-2,-1,0,3,2中选择一个合适的数,求此分式的值.
四.解答题(二)(本大题共3小题,每小题9分,共27分)
19.已知在平面直角坐标系中的位置如图所示,,,三点均在格点上.
(1)在直角坐标系内画出关于轴对称的△,并写出点,,的坐标;
(2)若点与点关于轴对称,则点的坐标为 ;
(3)如果要使与全等,那么点的坐标是 .
20.如图,在中,,,的垂直平分线分别交,于点,.
(1)求证:是等腰三角形;
(2)若的周长是13,,求的长.
21.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.
五.解答题(三)(本题共2小题,每小题12分,共24分)
22.在汕头市“创文”活动中,一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
(1)求乙工程队单独完成这项工作需要多少天?
(2)因工期的需要,将此项工程分成两部分,甲做其中一部分用了天完成,乙做另一部分用了天完成.若乙工程队还有其它工作任务,最多只能做52天.求甲工程队至少应做多少天?
23.如图1,直线AB分别与x轴、y轴交于A、B两点,OC平分∠AOB交AB于点C,点D为线段AB上一点,过点D作DE//OC交y轴于点E,已知AO=m,BO=n,且m、n满足n2-8n+16+|n-2m|=0.
(1)求A、B两点的坐标
(2)若点D为AB中点,求OE的长
(3)如图2,若点P(x,-2x+6)为直线AB在x轴下方的一点,点E是y轴的正半轴上一动点,以E为直角顶点作等腰直角△PEF,使点F在第一象限,且F点的横、纵坐标始终相等,求点P的坐标.
2022-2023八年级开学考试教学质量检测
___数学___学科答案
题 号 1 2 3 4 5 6 7 8 9 10
答案 D A C C B A B A C D
一.选择题(本题共10小题,每小题3分,共30分)
1.2022年卡塔尔世界杯是自1930年以来举办的第22届世界杯,历届世界杯可谓各具特色,会徽设计也蕴含了不同的文化.下列世界杯会徽的图案中,属于轴对称图形的是
A. B. C. D.
2.作为“广元七绝”之一绝的青川黑木耳因其朵大质厚、色泽深邃、细质滑美的特点被人们喜爱.黑木耳属于菌类,已知某种真菌的直径为,将该数据用科学记数法可以表示为
A. B. C. D.
3.如图,已知,,要使,添加的条件可以是
A. B. C. D.
4.已知等腰三角形的一个角为,则该三角形的顶角为
A. B. C.或 D.以上都不对
5.分式的值为零,则的值为
A. B.2 C. D.0或2
6.在平面直角坐标系中,点关于轴的对称点的坐标是
. . . .
7.下列长度的三条线段首尾相接不能围成三角形的是
A.2,3,4 B.8,7,15 C.6,8,10 D.13,12,20
8.从边长为的正方形中去掉一个边长为的小正方形,如图,然后将剩余部分剪后拼成一个矩形,上述操作所能验证的等式是( )
A. B.
C. D.
9.已知满足,则的值为( )
A.1 B.-5 C.-3 D.-7
10.如图,在△ABC中,∠B=32°,将△ABC沿直线翻折,点B落在点D的位置,
的度数是( )
A. B. C. D.
(
第10题图
)
题 号 11 12 13 14 15
答案 3(a+3)(a-3) 30° 80;L 20
二.填空题(本题共5小题,每小题3分,共15分)
11.分解因式: .
12.如图,在中,,以点为圆心,长为半径作弧,交直线于点,连结,则的度数是 .
13.在中,,,则 .
14.如图,点为内一点,分别作出点关于、的对称点,,连接交于,交于,,则的周长为 .
15.如图,已知△ABC的面积为1,分别倍长(延长一倍)边AB,BC,CA得到△A1B1C1,再分别倍长边A1B1,B1C1,C1A1得到△A2B2C2…按此规律,倍长2023次后得到的△A2023B2023C2023的面积为_________.
三.解答题(一)(本大题共3小题,每小题8分,共24分)
16.计算:.
解: 2’
2’
2’
1’
. 1’
17.解分式方程:.
解:,
方程两边同时乘以得: 2’
, 2’
解得:, 2’
检验:当时,, 1’
所以是原方程的根. 1’
18.先化简,再求值:请从-2,-1,0,3,2中选择一个合适的数,求此分式的值.
解:
,
∵ a≠0且a≠±2,a≠-1,
∴ a=3,
则原式=.
四.解答题(二)(本大题共3小题,每小题9分,共27分)
19.已知在平面直角坐标系中的位置如图所示,,,三点均在格点上.
(1)在直角坐标系内画出关于轴对称的△,并写出点,,的坐标;
(2)若点与点关于轴对称,则点的坐标为 ;
(3)如果要使与全等,那么点的坐标是 .
解:(1)如图所示:△即为所求,,,; 3’
(2)点与点关于轴对称,,
点的坐标为;
故答案为:; 3’
(3)要使与全等,则点的坐标是或或.
故答案为:或或. 3’
20.如图,在中,,,的垂直平分线分别交,于点,.
(1)求证:是等腰三角形;
(2)若的周长是13,,求的长.
(1)证明:,,
,
是的垂直平分线,
,
,
,
,
,
是等腰三角形;
(2)解:的周长是13,
,
,
,
,
,
,
,
21.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.
(1)证明:∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)解:∵△BDE≌△CEF,
∴∠BDE=∠CEF,
∴∠BED+∠CEF=∠BED+∠BDE,
∵∠B+(∠BED+∠BDE)=180°,
∠DEF+(∠BED+∠BDE)=180°,
∴∠B=∠DEF,
∵∠A=50°,AB=AC,
∴∠B=(180°﹣50°)=65°,
∴∠DEF=65°.
+
五.解答题(三)(本题共2小题,每小题12分,共24分)
22.在汕头市“创文”活动中,一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
(1)求乙工程队单独完成这项工作需要多少天?
(2)因工期的需要,将此项工程分成两部分,甲做其中一部分用了天完成,乙做另一部分用了天完成.若乙工程队还有其它工作任务,最多只能做52天.求甲工程队至少应做多少天?
(1)设乙工程队单独完成这项工作需要x天,由题意得:
解得:x=80, 经检验x=80是原方程的解.
答:乙工程队单独做需要80天完成.
(2)因为甲工程队做其中一部分用了天,乙工程队做另一部分用了天,
依题意得:,∴ .
∵ ,
∴ ,
解得:.
答:甲工程队至少应做42天.
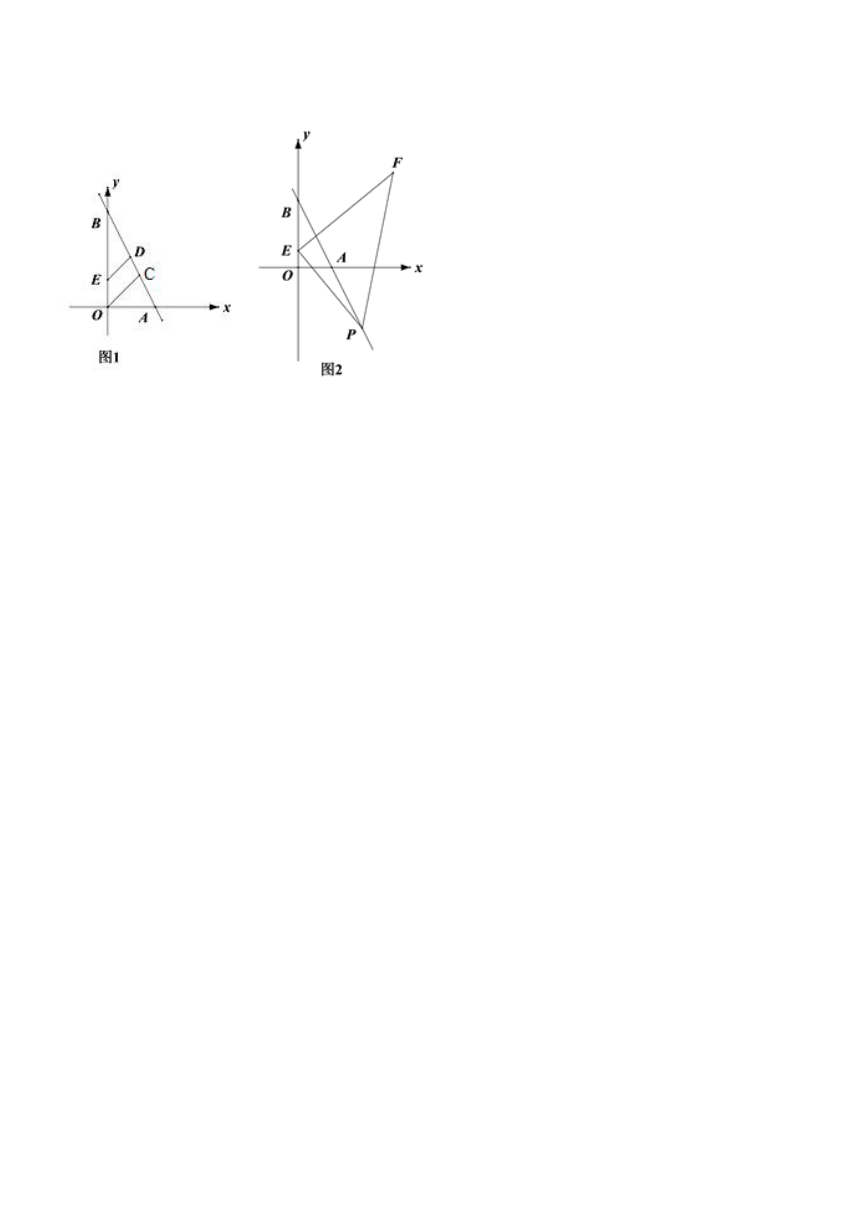
23.如图1,直线AB分别与x轴、y轴交于A、B两点,OC平分∠AOB交AB于点C,点D为线段AB上一点,过点D作DE//OC交y轴于点E,已知AO=m,BO=n,且m、n满足n2-8n+16+|n-2m|=0.
(1)求A、B两点的坐标
(2)若点D为AB中点,求OE的长
(3)如图2,若点P(x,-2x+6)为直线AB在x轴下方的一点,点E是y轴的正半轴上一动点,以E为直角顶点作等腰直角△PEF,使点F在第一象限,且F点的横、纵坐标始终相等,求点P的坐标.
解:(1)∵
∴
∵ ,
∴ ,
∴ m=2,n=4
∴ 点A为(2,0),点B为(0,4)
(2)延长DE交x轴于点F,延长FD到点G,使得DG=DF,连接BG
设OE=x
∵ OC平分∠AOB
∴∠ BOC=∠AOC=45°
∵ DE∥OC
∴ ∠EFO=∠FEO=∠BEG=∠BOC=∠AOC=45°
∴ OE=OF=x
在△ADF和△BDG中
∵
∴ △ADF≌△BDG(SAS)
∴ BG=AF=2+x,∠G=∠AFE=45°
∴ ∠G=∠BEG=45°
∴ BG=BE=4-x
∴ 4-x=2+x
解得:x=1
∴ OE=1
(3)(3)分别过点F、P作FM⊥y轴于点M,PN⊥y轴于点N
设点E为(0,m)
∵ 点P的坐标为(x,-2x+6)
则PN=x,EN=m+2x-6
∵ ∠PEF=90°
∴ ∠PEN+∠FEM=90°
∵ FM⊥y轴
∴ ∠MFE+∠FEM=90°
∴ ∠PEN=∠MFE
在△EFM和△PEN中
∵
∴ △EFM≌△PEN(AAS)
∴ ME=NP=x,FM=EN=m+2x-6
∴ 点F为(m+2x-6,m+x)
∵ F点的横坐标与纵坐标相等
∴ m+2x-6=m+x
解得:x=6
∴ 点P为(6,-6)
初二数学
一.选择题(本题共10小题,每小题3分,共30分)
1.2022年卡塔尔世界杯举办的第22届世界杯,历届世界杯可谓各具特色,会徽设计也蕴含了不同的文化.下列世界杯会徽的图案中,属于轴对称图形的是
A. B. C. D.
2.作为“广元七绝”之一绝的青川黑木耳因其朵大质厚、色泽深邃、细质滑美的特点被人们喜爱.黑木耳属于菌类,已知某种真菌的直径为,将该数据用科学记数法可以表示为
A. B. C. D.
3.如图,已知,,要使,添加的条件可以是
A. B. C. D.
4.已知等腰三角形的一个角为,则该三角形的顶角为
A. B. C.或 D.以上都不对
5.分式的值为零,则的值为
A. B.2 C. D.0或2
6.在平面直角坐标系中,点关于轴的对称点的坐标是
. . . .
7.下列长度的三条线段首尾相接不能围成三角形的是
A.2,3,4 B.8,7,15 C.6,8,10 D.13,12,20
8.从边长为的正方形中去掉一个边长为的小正方形,如图,然后将剩余部分剪后拼成一个矩形,上述操作所能验证的等式是( )
A. B.
C. D.
9.已知满足,则的值为( )
A.1 B.-5 C.-3 D.-7
10.如图,在△ABC中,∠B=32°,将△ABC沿直线翻折,点B落在点D的位置,则
的度数是( )
A. B. C. D.
二.填空题(本题共5小题,每小题3分,共15分)
11.分解因式: .
12.如图,在中,,以点为圆心,长为半径作弧,交直线于点,连结,则的度数是 .
13.在中,,,则 .
14.如图,点为内一点,分别作出点关于、的对称点,,连接交于,交于,,则的周长为 .
15.如图,已知△ABC的面积为1,分别倍长(延长一倍)边AB,BC,CA得到△A1B1C1,再分别倍长边A1B1,B1C1,C1A1得到△A2B2C2…按此规律,倍长2023次后得到的△A2023B2023C2023的面积为_________.
三.解答题(一)(本大题共3小题,每小题8分,共24分)
16.计算:.
17.解分式方程:.
18.先化简,再求值:请从-2,-1,0,3,2中选择一个合适的数,求此分式的值.
四.解答题(二)(本大题共3小题,每小题9分,共27分)
19.已知在平面直角坐标系中的位置如图所示,,,三点均在格点上.
(1)在直角坐标系内画出关于轴对称的△,并写出点,,的坐标;
(2)若点与点关于轴对称,则点的坐标为 ;
(3)如果要使与全等,那么点的坐标是 .
20.如图,在中,,,的垂直平分线分别交,于点,.
(1)求证:是等腰三角形;
(2)若的周长是13,,求的长.
21.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.
五.解答题(三)(本题共2小题,每小题12分,共24分)
22.在汕头市“创文”活动中,一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
(1)求乙工程队单独完成这项工作需要多少天?
(2)因工期的需要,将此项工程分成两部分,甲做其中一部分用了天完成,乙做另一部分用了天完成.若乙工程队还有其它工作任务,最多只能做52天.求甲工程队至少应做多少天?
23.如图1,直线AB分别与x轴、y轴交于A、B两点,OC平分∠AOB交AB于点C,点D为线段AB上一点,过点D作DE//OC交y轴于点E,已知AO=m,BO=n,且m、n满足n2-8n+16+|n-2m|=0.
(1)求A、B两点的坐标
(2)若点D为AB中点,求OE的长
(3)如图2,若点P(x,-2x+6)为直线AB在x轴下方的一点,点E是y轴的正半轴上一动点,以E为直角顶点作等腰直角△PEF,使点F在第一象限,且F点的横、纵坐标始终相等,求点P的坐标.
2022-2023八年级开学考试教学质量检测
___数学___学科答案
题 号 1 2 3 4 5 6 7 8 9 10
答案 D A C C B A B A C D
一.选择题(本题共10小题,每小题3分,共30分)
1.2022年卡塔尔世界杯是自1930年以来举办的第22届世界杯,历届世界杯可谓各具特色,会徽设计也蕴含了不同的文化.下列世界杯会徽的图案中,属于轴对称图形的是
A. B. C. D.
2.作为“广元七绝”之一绝的青川黑木耳因其朵大质厚、色泽深邃、细质滑美的特点被人们喜爱.黑木耳属于菌类,已知某种真菌的直径为,将该数据用科学记数法可以表示为
A. B. C. D.
3.如图,已知,,要使,添加的条件可以是
A. B. C. D.
4.已知等腰三角形的一个角为,则该三角形的顶角为
A. B. C.或 D.以上都不对
5.分式的值为零,则的值为
A. B.2 C. D.0或2
6.在平面直角坐标系中,点关于轴的对称点的坐标是
. . . .
7.下列长度的三条线段首尾相接不能围成三角形的是
A.2,3,4 B.8,7,15 C.6,8,10 D.13,12,20
8.从边长为的正方形中去掉一个边长为的小正方形,如图,然后将剩余部分剪后拼成一个矩形,上述操作所能验证的等式是( )
A. B.
C. D.
9.已知满足,则的值为( )
A.1 B.-5 C.-3 D.-7
10.如图,在△ABC中,∠B=32°,将△ABC沿直线翻折,点B落在点D的位置,
的度数是( )
A. B. C. D.
(
第10题图
)
题 号 11 12 13 14 15
答案 3(a+3)(a-3) 30° 80;L 20
二.填空题(本题共5小题,每小题3分,共15分)
11.分解因式: .
12.如图,在中,,以点为圆心,长为半径作弧,交直线于点,连结,则的度数是 .
13.在中,,,则 .
14.如图,点为内一点,分别作出点关于、的对称点,,连接交于,交于,,则的周长为 .
15.如图,已知△ABC的面积为1,分别倍长(延长一倍)边AB,BC,CA得到△A1B1C1,再分别倍长边A1B1,B1C1,C1A1得到△A2B2C2…按此规律,倍长2023次后得到的△A2023B2023C2023的面积为_________.
三.解答题(一)(本大题共3小题,每小题8分,共24分)
16.计算:.
解: 2’
2’
2’
1’
. 1’
17.解分式方程:.
解:,
方程两边同时乘以得: 2’
, 2’
解得:, 2’
检验:当时,, 1’
所以是原方程的根. 1’
18.先化简,再求值:请从-2,-1,0,3,2中选择一个合适的数,求此分式的值.
解:
,
∵ a≠0且a≠±2,a≠-1,
∴ a=3,
则原式=.
四.解答题(二)(本大题共3小题,每小题9分,共27分)
19.已知在平面直角坐标系中的位置如图所示,,,三点均在格点上.
(1)在直角坐标系内画出关于轴对称的△,并写出点,,的坐标;
(2)若点与点关于轴对称,则点的坐标为 ;
(3)如果要使与全等,那么点的坐标是 .
解:(1)如图所示:△即为所求,,,; 3’
(2)点与点关于轴对称,,
点的坐标为;
故答案为:; 3’
(3)要使与全等,则点的坐标是或或.
故答案为:或或. 3’
20.如图,在中,,,的垂直平分线分别交,于点,.
(1)求证:是等腰三角形;
(2)若的周长是13,,求的长.
(1)证明:,,
,
是的垂直平分线,
,
,
,
,
,
是等腰三角形;
(2)解:的周长是13,
,
,
,
,
,
,
,
21.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.
(1)证明:∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)解:∵△BDE≌△CEF,
∴∠BDE=∠CEF,
∴∠BED+∠CEF=∠BED+∠BDE,
∵∠B+(∠BED+∠BDE)=180°,
∠DEF+(∠BED+∠BDE)=180°,
∴∠B=∠DEF,
∵∠A=50°,AB=AC,
∴∠B=(180°﹣50°)=65°,
∴∠DEF=65°.
+
五.解答题(三)(本题共2小题,每小题12分,共24分)
22.在汕头市“创文”活动中,一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
(1)求乙工程队单独完成这项工作需要多少天?
(2)因工期的需要,将此项工程分成两部分,甲做其中一部分用了天完成,乙做另一部分用了天完成.若乙工程队还有其它工作任务,最多只能做52天.求甲工程队至少应做多少天?
(1)设乙工程队单独完成这项工作需要x天,由题意得:
解得:x=80, 经检验x=80是原方程的解.
答:乙工程队单独做需要80天完成.
(2)因为甲工程队做其中一部分用了天,乙工程队做另一部分用了天,
依题意得:,∴ .
∵ ,
∴ ,
解得:.
答:甲工程队至少应做42天.
23.如图1,直线AB分别与x轴、y轴交于A、B两点,OC平分∠AOB交AB于点C,点D为线段AB上一点,过点D作DE//OC交y轴于点E,已知AO=m,BO=n,且m、n满足n2-8n+16+|n-2m|=0.
(1)求A、B两点的坐标
(2)若点D为AB中点,求OE的长
(3)如图2,若点P(x,-2x+6)为直线AB在x轴下方的一点,点E是y轴的正半轴上一动点,以E为直角顶点作等腰直角△PEF,使点F在第一象限,且F点的横、纵坐标始终相等,求点P的坐标.
解:(1)∵
∴
∵ ,
∴ ,
∴ m=2,n=4
∴ 点A为(2,0),点B为(0,4)
(2)延长DE交x轴于点F,延长FD到点G,使得DG=DF,连接BG
设OE=x
∵ OC平分∠AOB
∴∠ BOC=∠AOC=45°
∵ DE∥OC
∴ ∠EFO=∠FEO=∠BEG=∠BOC=∠AOC=45°
∴ OE=OF=x
在△ADF和△BDG中
∵
∴ △ADF≌△BDG(SAS)
∴ BG=AF=2+x,∠G=∠AFE=45°
∴ ∠G=∠BEG=45°
∴ BG=BE=4-x
∴ 4-x=2+x
解得:x=1
∴ OE=1
(3)(3)分别过点F、P作FM⊥y轴于点M,PN⊥y轴于点N
设点E为(0,m)
∵ 点P的坐标为(x,-2x+6)
则PN=x,EN=m+2x-6
∵ ∠PEF=90°
∴ ∠PEN+∠FEM=90°
∵ FM⊥y轴
∴ ∠MFE+∠FEM=90°
∴ ∠PEN=∠MFE
在△EFM和△PEN中
∵
∴ △EFM≌△PEN(AAS)
∴ ME=NP=x,FM=EN=m+2x-6
∴ 点F为(m+2x-6,m+x)
∵ F点的横坐标与纵坐标相等
∴ m+2x-6=m+x
解得:x=6
∴ 点P为(6,-6)
同课章节目录
