数学人教A版(2019)选择性必修第一册3.2.2 双曲线的简单几何性质(共22张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.2.2 双曲线的简单几何性质(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-10 22:26:35 | ||
图片预览







文档简介
(共22张PPT)
3.2.2 双曲线的简单几何性质
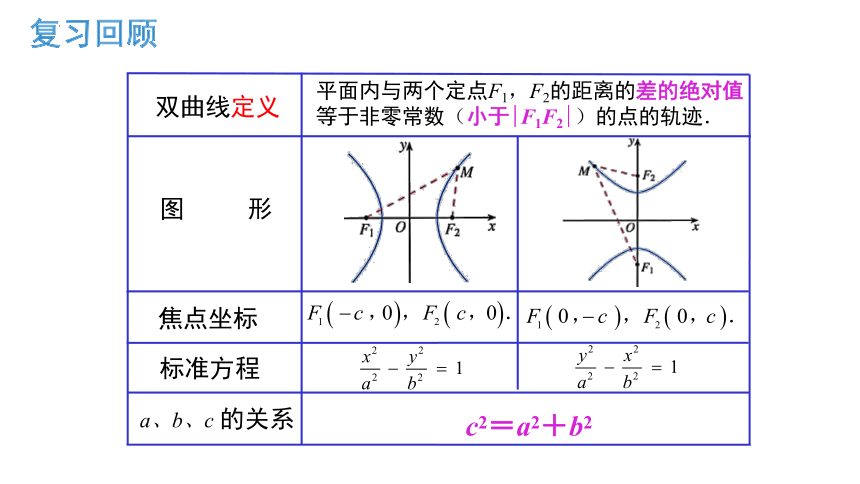
标准方程
图 形
焦点坐标
双曲线定义
a、b、c 的关系
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹.
复习回顾
c2=a2+b2
思考:类比对椭圆几何性质的研究,你认为应该研究双曲线的哪些几何性质?如何研究这些性质?
范围、对称性、顶点、离心率…
利用双曲线的标准方程研究双曲线的几何性质
以
(a>0,b>0)为例
1.范围
a
-a
O
x
F1
F2
y
于是双曲线上的点都满足不等式,
由双曲线的标准方程可知,
即,
所以或
双曲线在不等式所表示的区域内.
y
O
x
F1
F2
2.对称性
从图形上看:双曲线既是轴对称图形,又是中心对称图形
①
轴
②
轴
③
原点
双曲线关于x轴、y轴和原点对称.坐标轴是双曲线的对称轴,原点是双曲线的对称中心,双曲线的对称中心叫做双曲线的中心.
从方程上看:
3.顶点
观察双曲线,你觉得有哪些比较特殊的点?
双曲线与x轴的交点:
双曲线与y轴的交点:
y
O
x
A1
A2
F1
F2
y=b
y=-b
B2
B1
令
令得,
方程无实数根,则双曲线与y轴无交点.
双曲线的两个顶点坐标为,
双曲线的实轴:
双曲线的虚轴:
双曲线的焦距:
为实半轴长;
为虚半轴长;
为半焦距.
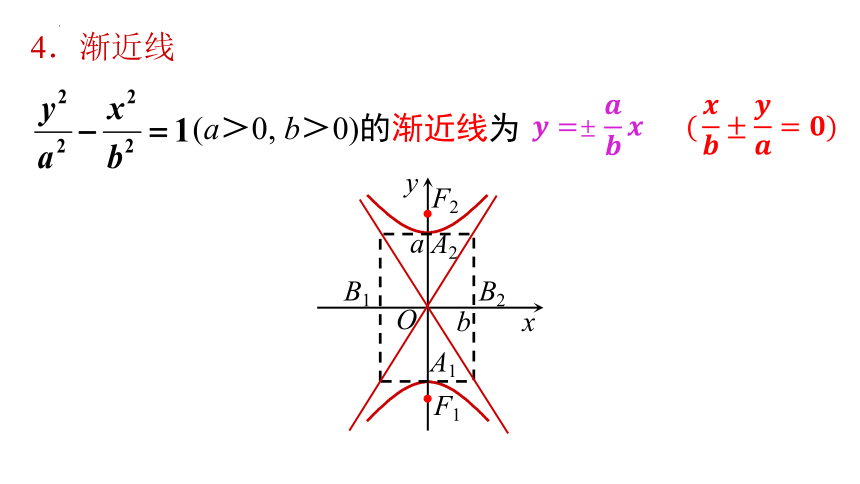
4.渐近线
活动:利用信息技术画出双曲线 和两条直线 .在双曲线的右支上取一点 ,测量点 的横坐标 以及它到直线 的距离 .沿曲线向右上方拖动点 ,观察 与 的大小关系,你发现了什么?
4.渐近线
经过, 作轴的平行线 ,经过, 作 轴的平行线,四条直线围成一个矩形 (如图).
y
O
x
A1
A2
B2
B1
F1
F2
a
b
叫做双曲线的渐近线.
两条直线:
图像特征:双曲线与它的渐近线无限接近,但永不相交.
4.渐近线
(a>0, b>0)的渐近线为
y
O
x
A1
A2
B2
B1
a
b
F1
F2
4.渐近线
这时双曲线方程为x2-y2=a2,实轴长和虚轴长都为,渐近线方程为y=±x,它们互相垂直,并且平分双曲线实轴和虚轴所成的角.
当a=b时,实轴和虚轴等长,这样的双曲线叫等轴双曲线.
利用渐近线画双曲线草图
⑴ 画出双曲线的渐近线;
⑵ 画出双曲线的顶点、第一象限内双曲线的大致图象;
⑶ 利用双曲线的对称性画出完整双曲线.
6.通径
双曲线的焦距与实轴长的比 ,
叫做双曲线的离心率.
因为 c >a>0,
所以e>1.
双曲线的离心率刻画了什么几何特征呢?
双曲线的离心率越大,它的张口就越大.
5.离心率
F1
F2
x
y
O
A
B
通径
例3 求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
双曲线标准方程
焦点位置 焦点在x轴上 焦点在y轴上
图形
范围
对称性
顶点
轴长
渐近线
离心率
()
()
关于x轴、y轴对称,关于原点中心对称
实轴长为,虚轴长为
直线
直线
()
例4 双曲线冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小半径为12m,上口半径为13m,下口半径为25m,高为55m,试建立适当的坐标系,求出此双曲线的方程(精确到1m).
解:根据双曲线的对称性,在冷却塔的轴截面所在平面建立如图所示的平面直角坐标系Oxy,使小圆的直径AA’在x轴上,圆心与原点重合.
设双曲线的方程为
因此所求曲线方程为
得19b2+275b-18150=0 ,解得b≈25
由方程②,得
代入方程①并化简
所以
C(13,y),B(25,y-55)
M
x
y
O
H
F
d
例5 点与定点的距离和它到直线的距离的比是常数,求点的轨迹.
例6 如图所示,过双曲线的右焦点,倾斜角为30°的直线交双曲线于两点,求||.
F1
F2
x
y
O
A
B
3.2.2 双曲线的简单几何性质
标准方程
图 形
焦点坐标
双曲线定义
a、b、c 的关系
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹.
复习回顾
c2=a2+b2
思考:类比对椭圆几何性质的研究,你认为应该研究双曲线的哪些几何性质?如何研究这些性质?
范围、对称性、顶点、离心率…
利用双曲线的标准方程研究双曲线的几何性质
以
(a>0,b>0)为例
1.范围
a
-a
O
x
F1
F2
y
于是双曲线上的点都满足不等式,
由双曲线的标准方程可知,
即,
所以或
双曲线在不等式所表示的区域内.
y
O
x
F1
F2
2.对称性
从图形上看:双曲线既是轴对称图形,又是中心对称图形
①
轴
②
轴
③
原点
双曲线关于x轴、y轴和原点对称.坐标轴是双曲线的对称轴,原点是双曲线的对称中心,双曲线的对称中心叫做双曲线的中心.
从方程上看:
3.顶点
观察双曲线,你觉得有哪些比较特殊的点?
双曲线与x轴的交点:
双曲线与y轴的交点:
y
O
x
A1
A2
F1
F2
y=b
y=-b
B2
B1
令
令得,
方程无实数根,则双曲线与y轴无交点.
双曲线的两个顶点坐标为,
双曲线的实轴:
双曲线的虚轴:
双曲线的焦距:
为实半轴长;
为虚半轴长;
为半焦距.
4.渐近线
活动:利用信息技术画出双曲线 和两条直线 .在双曲线的右支上取一点 ,测量点 的横坐标 以及它到直线 的距离 .沿曲线向右上方拖动点 ,观察 与 的大小关系,你发现了什么?
4.渐近线
经过, 作轴的平行线 ,经过, 作 轴的平行线,四条直线围成一个矩形 (如图).
y
O
x
A1
A2
B2
B1
F1
F2
a
b
叫做双曲线的渐近线.
两条直线:
图像特征:双曲线与它的渐近线无限接近,但永不相交.
4.渐近线
(a>0, b>0)的渐近线为
y
O
x
A1
A2
B2
B1
a
b
F1
F2
4.渐近线
这时双曲线方程为x2-y2=a2,实轴长和虚轴长都为,渐近线方程为y=±x,它们互相垂直,并且平分双曲线实轴和虚轴所成的角.
当a=b时,实轴和虚轴等长,这样的双曲线叫等轴双曲线.
利用渐近线画双曲线草图
⑴ 画出双曲线的渐近线;
⑵ 画出双曲线的顶点、第一象限内双曲线的大致图象;
⑶ 利用双曲线的对称性画出完整双曲线.
6.通径
双曲线的焦距与实轴长的比 ,
叫做双曲线的离心率.
因为 c >a>0,
所以e>1.
双曲线的离心率刻画了什么几何特征呢?
双曲线的离心率越大,它的张口就越大.
5.离心率
F1
F2
x
y
O
A
B
通径
例3 求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
双曲线标准方程
焦点位置 焦点在x轴上 焦点在y轴上
图形
范围
对称性
顶点
轴长
渐近线
离心率
()
()
关于x轴、y轴对称,关于原点中心对称
实轴长为,虚轴长为
直线
直线
()
例4 双曲线冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小半径为12m,上口半径为13m,下口半径为25m,高为55m,试建立适当的坐标系,求出此双曲线的方程(精确到1m).
解:根据双曲线的对称性,在冷却塔的轴截面所在平面建立如图所示的平面直角坐标系Oxy,使小圆的直径AA’在x轴上,圆心与原点重合.
设双曲线的方程为
因此所求曲线方程为
得19b2+275b-18150=0 ,解得b≈25
由方程②,得
代入方程①并化简
所以
C(13,y),B(25,y-55)
M
x
y
O
H
F
d
例5 点与定点的距离和它到直线的距离的比是常数,求点的轨迹.
例6 如图所示,过双曲线的右焦点,倾斜角为30°的直线交双曲线于两点,求||.
F1
F2
x
y
O
A
B
