17.2.2 勾股定理逆定理的应用
文档属性
| 名称 | 17.2.2 勾股定理逆定理的应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 753.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-16 00:00:00 | ||
图片预览




文档简介
课件13张PPT。17.2.2勾股定理的逆定理(2)2014年3月12日 说一说:1.勾股定理的逆定理内容是什么?
2. 它与勾股定理的联系与区别.回顾与复习 勾股定理的逆定理:
如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是直角三角形.1. 判断由线段a、b、c组成的三角形是不是直角三角形。① a=7, b=24, c=25??④ a=40, b=50, c=60回顾与复习 √√√×回顾与复习 2. 下列各命题都成立,写出它们的逆命题。这些逆命题成立吗?① 同旁内角互补,两直线平行;
② 如果两个角是直角,那么它们相等;
③ 全等三角形的对应边相等;
④ 如果两个实数相等,那么它们的平方相等。
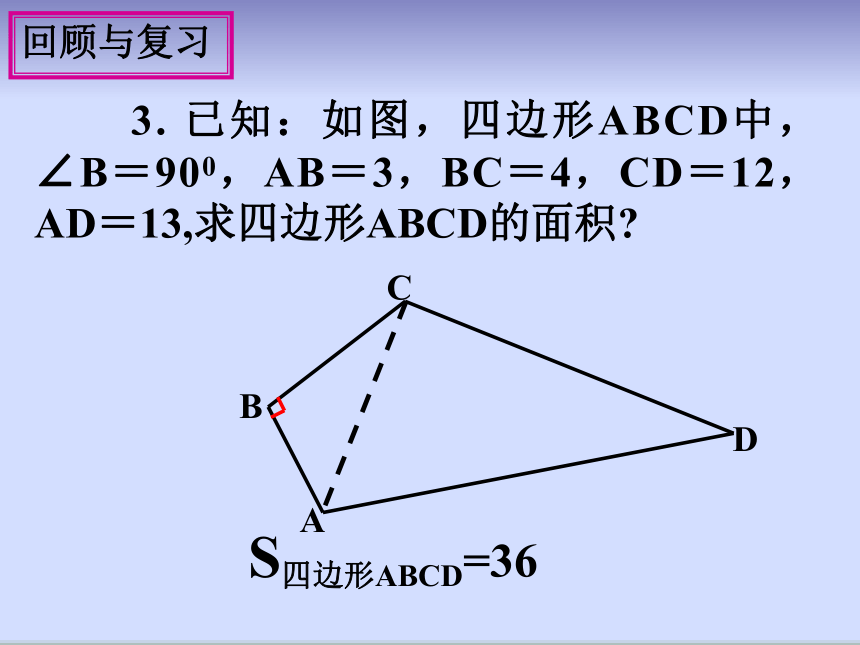
3. 已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?
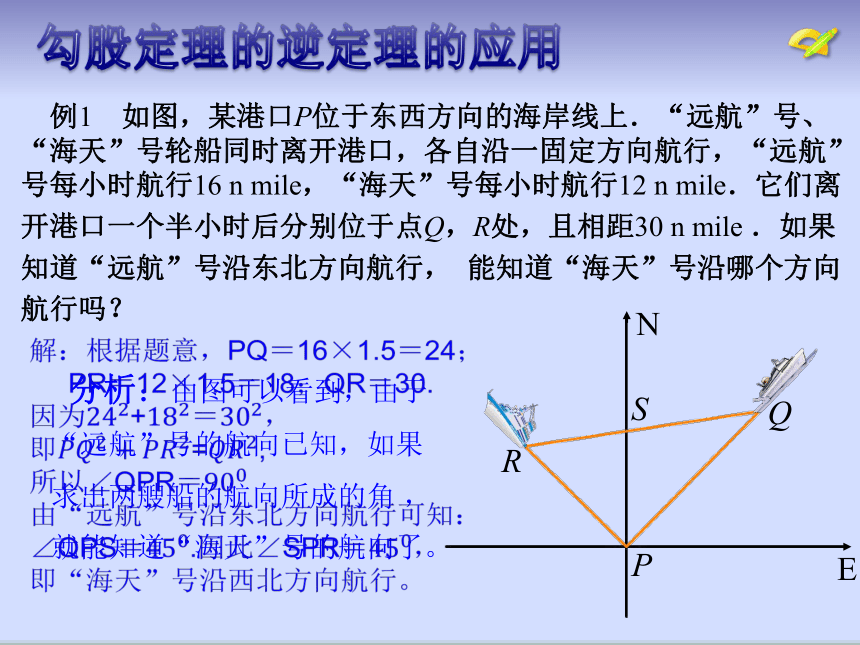
S四边形ABCD=36回顾与复习 例1 如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航” 号每小时航行16 n mile,“海天”号每小时航行12 n mile.它们离
开港口一个半小时后分别位于点Q,R处,且相距30 n mile .如果
知道“远航”号沿东北方向航行, 能知道“海天”号沿哪个方向
航行吗? 分析:由图可以看到,由于“远航”号的航向已知,如果求出两艘船的航向所成的角 ,就能知道“海天”号的航向了。?勾股定理的逆定理的应用 例2:已知:如图,正方形ABCD中,AB=4cm.点E是
BC的中点,点F是CD上一点,且 .
求证:∠AEF=90°. 引申:
若去掉上题中的条件“AB=4cm”,结论还成立吗?勾股定理的逆定理的应用基础巩固1.完成课本第33页“练习”第3题。2.若△ABC的三边a、b、c,满足(a-b)(a2+b2-c2)=0,则△ABC是( )
A.等腰三角形;
B.直角三角形;
C.等腰三角形或直角三角形;
D.等腰直角三角形。C
?ABCD基础巩固S四边形ABCD=24提高作业?? 3. 如图,南北向MN为我国领域,即MN以西为我国领海,以东为公海. 上午9时50分,我反走私艇A发现正东方向有一走私艇C以13海里/时的速度偷偷向我领海开来,便立即通知正在MN线上巡逻的我国反走私艇B.已知A、C 两艇的距离是13海里, A、B两艇的距离是5海里 ;反走私艇B测得离C艇的距离是12海里.若走私艇C的速度不变,最早会在什么时间进入我国领海??提高作业分析:先来判断a,b,c三边哪条最长,可以代m,n为满足条件的特殊值来试,m=5,n=4.则a=9,b=40,c=41,c最大。∴△ABC是直角三角形提高作业再见
2. 它与勾股定理的联系与区别.回顾与复习 勾股定理的逆定理:
如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是直角三角形.1. 判断由线段a、b、c组成的三角形是不是直角三角形。① a=7, b=24, c=25??④ a=40, b=50, c=60回顾与复习 √√√×回顾与复习 2. 下列各命题都成立,写出它们的逆命题。这些逆命题成立吗?① 同旁内角互补,两直线平行;
② 如果两个角是直角,那么它们相等;
③ 全等三角形的对应边相等;
④ 如果两个实数相等,那么它们的平方相等。
3. 已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?
S四边形ABCD=36回顾与复习 例1 如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航” 号每小时航行16 n mile,“海天”号每小时航行12 n mile.它们离
开港口一个半小时后分别位于点Q,R处,且相距30 n mile .如果
知道“远航”号沿东北方向航行, 能知道“海天”号沿哪个方向
航行吗? 分析:由图可以看到,由于“远航”号的航向已知,如果求出两艘船的航向所成的角 ,就能知道“海天”号的航向了。?勾股定理的逆定理的应用 例2:已知:如图,正方形ABCD中,AB=4cm.点E是
BC的中点,点F是CD上一点,且 .
求证:∠AEF=90°. 引申:
若去掉上题中的条件“AB=4cm”,结论还成立吗?勾股定理的逆定理的应用基础巩固1.完成课本第33页“练习”第3题。2.若△ABC的三边a、b、c,满足(a-b)(a2+b2-c2)=0,则△ABC是( )
A.等腰三角形;
B.直角三角形;
C.等腰三角形或直角三角形;
D.等腰直角三角形。C
?ABCD基础巩固S四边形ABCD=24提高作业?? 3. 如图,南北向MN为我国领域,即MN以西为我国领海,以东为公海. 上午9时50分,我反走私艇A发现正东方向有一走私艇C以13海里/时的速度偷偷向我领海开来,便立即通知正在MN线上巡逻的我国反走私艇B.已知A、C 两艇的距离是13海里, A、B两艇的距离是5海里 ;反走私艇B测得离C艇的距离是12海里.若走私艇C的速度不变,最早会在什么时间进入我国领海??提高作业分析:先来判断a,b,c三边哪条最长,可以代m,n为满足条件的特殊值来试,m=5,n=4.则a=9,b=40,c=41,c最大。∴△ABC是直角三角形提高作业再见
