17.1.4勾股定理的应用
文档属性
| 名称 | 17.1.4勾股定理的应用 |  | |
| 格式 | pptx | ||
| 文件大小 | 151.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-16 17:00:17 | ||
图片预览


文档简介
(共16张PPT)
17.1.4勾股定理的应用(3)
1.在 ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______.
2.在 ABC中, C=90°,若AC=6,CB=8,则 ABC面积为_____,斜边为上的高为______.
6
8
41
24
4.8
复习
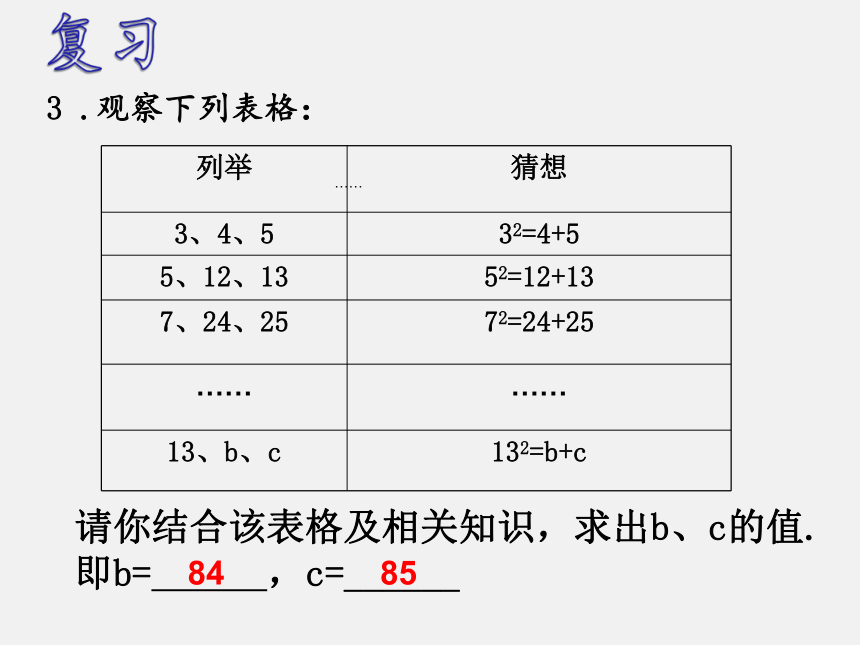
3 .观察下列表格:
……
列举 猜想
3、4、5 32=4+5
5、12、13 52=12+13
7、24、25 72=24+25
…… ……
13、b、c 132=b+c
请你结合该表格及相关知识,求出b、c的值.
即b= ,c=______
84
85
复习
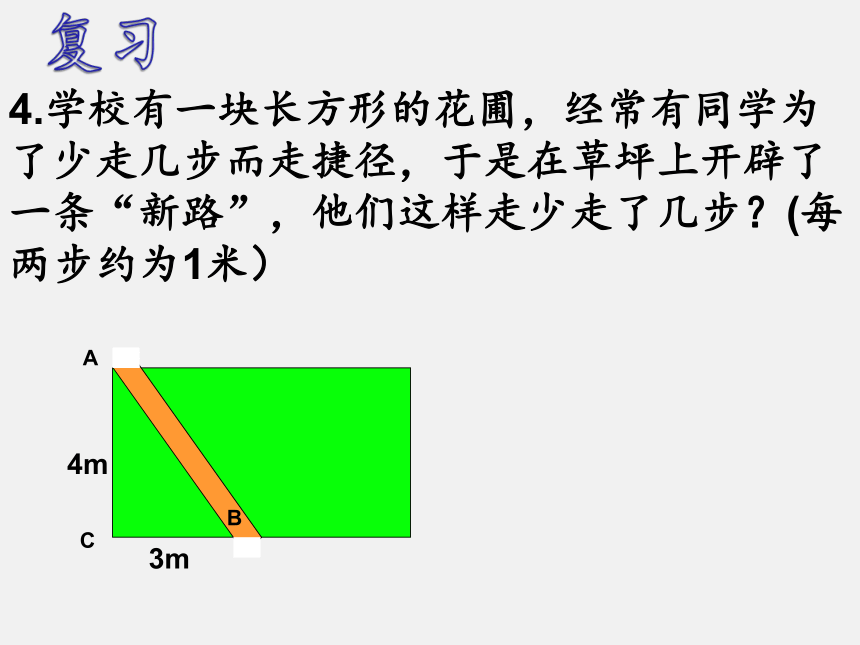
4.学校有一块长方形的花圃,经常有同学为了少走几步而走捷径,于是在草坪上开辟了一条“新路”,他们这样走少走了几步?(每两步约为1米)
4m
3m
A
B
C
复习
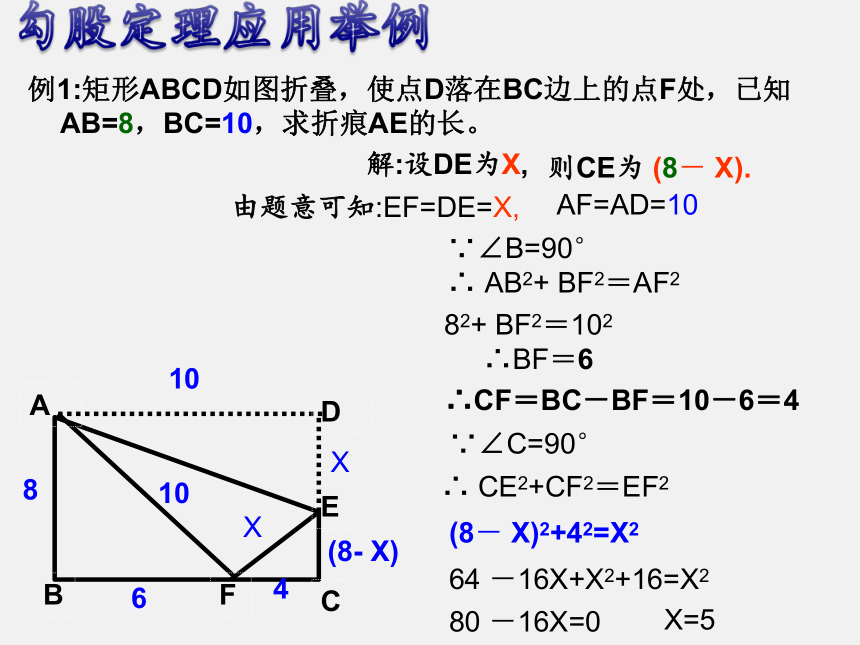
例1:矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。
A
B
C
D
F
E
解:设DE为X,
X
(8- X)
则CE为 (8- X).
由题意可知:EF=DE=X,
X
AF=AD=10
10
10
8
∵∠B=90°
∴ AB2+ BF2=AF2
82+ BF2=102
∴BF=6
∴CF=BC-BF=10-6=4
6
4
∵∠C=90°
∴ CE2+CF2=EF2
(8- X)2+42=X2
64 -16X+X2+16=X2
80 -16X=0
X=5
勾股定理应用举例
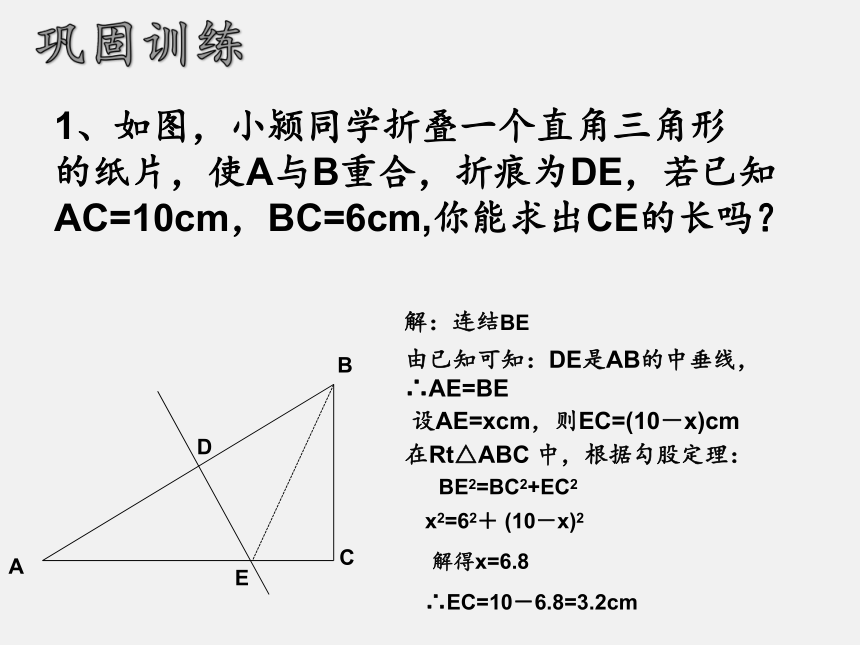
1、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
解:连结BE
由已知可知:DE是AB的中垂线,∴AE=BE
在Rt△ABC 中,根据勾股定理:
设AE=xcm,则EC=(10-x)cm
BE2=BC2+EC2
x2=62+ (10-x)2
解得x=6.8
∴EC=10-6.8=3.2cm
巩固训练
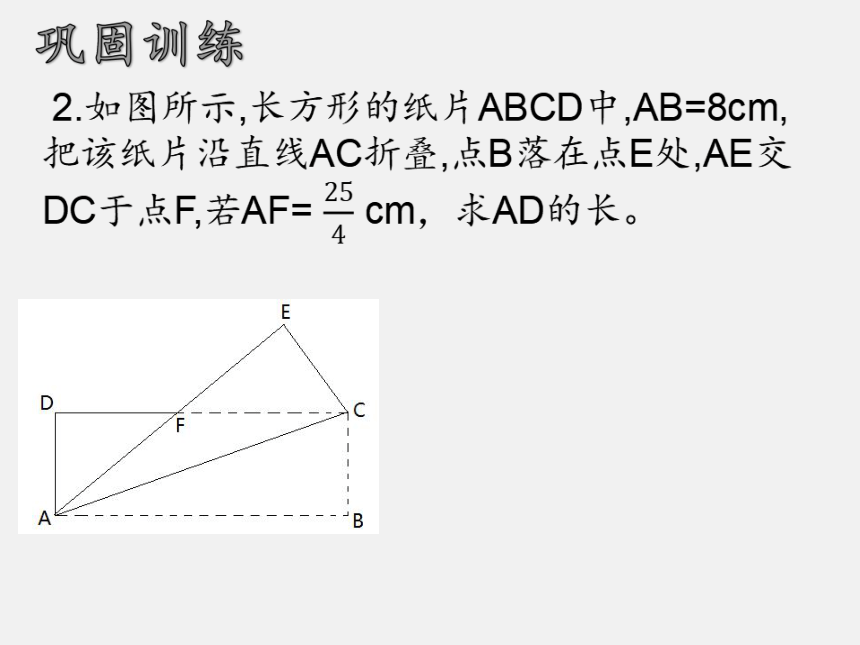
2.如图所示,长方形的纸片ABCD中,AB=8cm,把该纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,若AF= cm,求AD的长。
巩固训练
例2:已知,如图,Rt△ABC中,∠BAC=90°,AB=AC,D是BC上任意一点。
求证:1. BD2+CD2=2AD2.
2. AB2-AD2=BD·CD
E
勾股定理应用举例
引申:若点D在CB的延长线上,上述结论是否仍然成立?
如图,在Rt△ABC中,AB=AC,D点在CB延长线上。
A
B
C
D
E
引申:
BD2+CD2=2AD2.
AB2-AD2=BD·CD
A
B
C
A
C
P
A
C
巩固训练
如图所示,在△ABC中,AB=AC=4,P为BC上的一点,
(1)求证:
E
1.已知:如图,∠ABD=∠C=90°,AD=12,AC=BC,∠DAB=30°,求BC的长.
提高作业
2.如图,有一个直角三角形纸片,两直直角边AC=6cm,BC=8cm,现将直角边AC沿∠CAB的角平分线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
A
E
C
D
B
提高作业
A
B
C
D
E
F
3. 如右图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF=___________。
提高作业
4. 如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
C
A
E
B
D
提高作业
如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求以折痕EF为边长的正方形面积。
A
B
C
D
G
F
E
解:由已知AF=FC
设AF=x,则FB=9-x
在R t △ABC中,根据勾股定理FC2=FB2+BC2
则有x2=(9-x)2+32
解得x=5
同理可得DE=4
∴GF=1
∴以EF为边的正方形的面积=EG2+GF2=32+12=10
思考
再见
17.1.4勾股定理的应用(3)
1.在 ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______.
2.在 ABC中, C=90°,若AC=6,CB=8,则 ABC面积为_____,斜边为上的高为______.
6
8
41
24
4.8
复习
3 .观察下列表格:
……
列举 猜想
3、4、5 32=4+5
5、12、13 52=12+13
7、24、25 72=24+25
…… ……
13、b、c 132=b+c
请你结合该表格及相关知识,求出b、c的值.
即b= ,c=______
84
85
复习
4.学校有一块长方形的花圃,经常有同学为了少走几步而走捷径,于是在草坪上开辟了一条“新路”,他们这样走少走了几步?(每两步约为1米)
4m
3m
A
B
C
复习
例1:矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。
A
B
C
D
F
E
解:设DE为X,
X
(8- X)
则CE为 (8- X).
由题意可知:EF=DE=X,
X
AF=AD=10
10
10
8
∵∠B=90°
∴ AB2+ BF2=AF2
82+ BF2=102
∴BF=6
∴CF=BC-BF=10-6=4
6
4
∵∠C=90°
∴ CE2+CF2=EF2
(8- X)2+42=X2
64 -16X+X2+16=X2
80 -16X=0
X=5
勾股定理应用举例
1、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
解:连结BE
由已知可知:DE是AB的中垂线,∴AE=BE
在Rt△ABC 中,根据勾股定理:
设AE=xcm,则EC=(10-x)cm
BE2=BC2+EC2
x2=62+ (10-x)2
解得x=6.8
∴EC=10-6.8=3.2cm
巩固训练
2.如图所示,长方形的纸片ABCD中,AB=8cm,把该纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,若AF= cm,求AD的长。
巩固训练
例2:已知,如图,Rt△ABC中,∠BAC=90°,AB=AC,D是BC上任意一点。
求证:1. BD2+CD2=2AD2.
2. AB2-AD2=BD·CD
E
勾股定理应用举例
引申:若点D在CB的延长线上,上述结论是否仍然成立?
如图,在Rt△ABC中,AB=AC,D点在CB延长线上。
A
B
C
D
E
引申:
BD2+CD2=2AD2.
AB2-AD2=BD·CD
A
B
C
A
C
P
A
C
巩固训练
如图所示,在△ABC中,AB=AC=4,P为BC上的一点,
(1)求证:
E
1.已知:如图,∠ABD=∠C=90°,AD=12,AC=BC,∠DAB=30°,求BC的长.
提高作业
2.如图,有一个直角三角形纸片,两直直角边AC=6cm,BC=8cm,现将直角边AC沿∠CAB的角平分线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
A
E
C
D
B
提高作业
A
B
C
D
E
F
3. 如右图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF=___________。
提高作业
4. 如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
C
A
E
B
D
提高作业
如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求以折痕EF为边长的正方形面积。
A
B
C
D
G
F
E
解:由已知AF=FC
设AF=x,则FB=9-x
在R t △ABC中,根据勾股定理FC2=FB2+BC2
则有x2=(9-x)2+32
解得x=5
同理可得DE=4
∴GF=1
∴以EF为边的正方形的面积=EG2+GF2=32+12=10
思考
再见
