沪科版七年级下册数学 9.3.2分式方程的应用 课件(共13张PPT)
文档属性
| 名称 | 沪科版七年级下册数学 9.3.2分式方程的应用 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 413.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-10 00:00:00 | ||
图片预览




文档简介
(共13张PPT)
9.3 分式方程
第九章 分 式
第2课时 分式方程的应用
1.解分式方程的基本思路是?
2.解分式方程有哪几个步骤?
分式方程
整式方程
转化
去分母
一化二解三检验
3.我们现在所学过的应用题有哪几种类型?每种类型的基本公式是什么?
基本上有5种:
(1)行程问题: 路程=速度×时间以及它的两个变式;
(2)数字问题: 在数字问题中要掌握十进制数的表示法;
(3)工程问题: 工作总量=工作时间×工作效率以及它的两个变式;
(4)顺逆问题: 顺速=静速+水速;逆速=静速-水速;
(5)买卖问题: 总价=单价×数量以及它的两个变式;
列分式方程解决实际问题
一
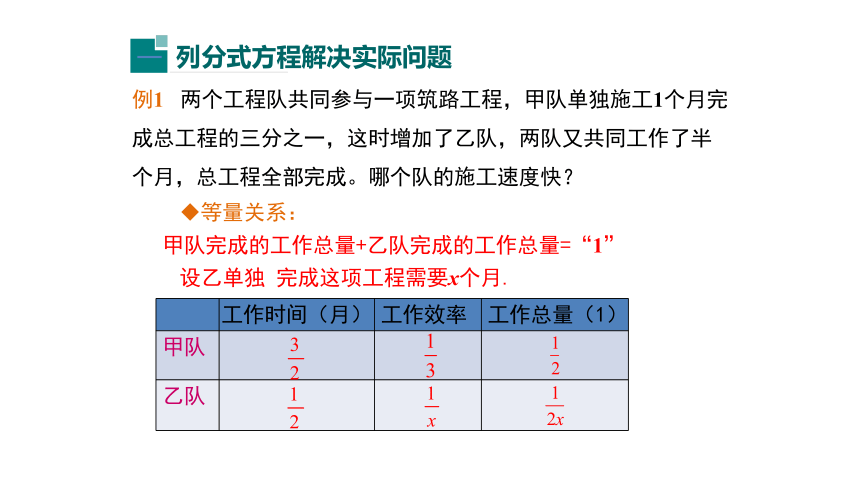
例1 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
工作时间(月) 工作效率 工作总量(1)
甲队
乙队
等量关系:
甲队完成的工作总量+乙队完成的工作总量=“1”
设乙单独 完成这项工程需要x个月.
解:设乙单独 完成这项工程需要x个月.根据题意得
方程两边都乘以6x,得
解得 x=1.
检验:当x=1时,6x≠0.
所以,原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,而甲队单独施工需3个月才可以完成全部任务,所以乙队的施工速度快.
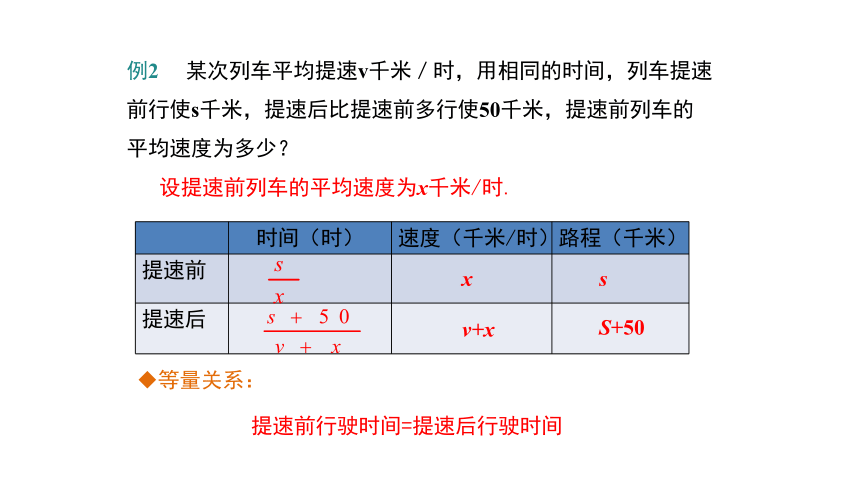
例2 某次列车平均提速v千米/时,用相同的时间,列车提速前行使s千米,提速后比提速前多行使50千米,提速前列车的平均速度为多少?
时间(时) 速度(千米/时) 路程(千米)
提速前
提速后
设提速前列车的平均速度为x千米/时.
s
v+x
S+50
x
等量关系:
提速前行驶时间=提速后行驶时间
解:设提速前列车的平均速度为x千米/时,根据题意得
解得
经检验:
x= 是原方程的解
答:提速前列车的速度为 千米/时.
列分式方程解应用题的一般步骤
1.审:审清题意,并设未知数
2.找:找出相等关系
3.列:列出方程
4.解:解这个分式方程;
5.验:既要检验根是否是所列分式方程的根,又要检验根是否符合题意;
6.写:写出答案.
当堂练习
1.某工程队需要在规定日期内完成.若甲队单独做正好按时完成;若乙队单独做,超过规定日期三天才能完成.现由甲、乙合作两天,余下工程由乙队单独做,恰好按期完成,问规定日期是多少天?
解;设规定日期是x天,根据题意,得:
方程两边同乘以x(x+3),得:
2(x+3)+x2=x(x+3)
解得: x=6
检验:x=6时x(x+3)≠0,x=6是原方程的解.
答:规定日期是6天.
2.一轮船往返于A、B两地之间,顺水比逆水快1小时到达.已知A、B两地相距80千米,水流速度是2千米/小时,求轮船在静水中的速度.
x=-18(不合题意,舍去),
解:设船在静水中的速度为x千米/小时,根据题意得
解得 x=±18.
检验得:x=18.
答:船在静水中的速度为18千米/小时.
方程两边同乘(x-2)(x+2)得
80x+160 -80x+160=x2 -4.
3. 某校师生到距学校15千米的景区游玩,一部分人骑自行车先走,过了40分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度.
解:设自行车的速度为x千米/时,那么汽车的速度是3x千米/时,依题意得:
解得
x=15.
经检验,x=15是原方程的根.
由x=15得3x=45.
答:自行车的速度是15千米/时,汽车的速度是45千米/时.
课堂小结
分式方程的应用
类型
行程问题、工程问题、数字问题、顺逆问题、买卖问题等
步骤
一审二设三找四列五解六验七写
习题9.3第5、6题
课后作业
9.3 分式方程
第九章 分 式
第2课时 分式方程的应用
1.解分式方程的基本思路是?
2.解分式方程有哪几个步骤?
分式方程
整式方程
转化
去分母
一化二解三检验
3.我们现在所学过的应用题有哪几种类型?每种类型的基本公式是什么?
基本上有5种:
(1)行程问题: 路程=速度×时间以及它的两个变式;
(2)数字问题: 在数字问题中要掌握十进制数的表示法;
(3)工程问题: 工作总量=工作时间×工作效率以及它的两个变式;
(4)顺逆问题: 顺速=静速+水速;逆速=静速-水速;
(5)买卖问题: 总价=单价×数量以及它的两个变式;
列分式方程解决实际问题
一
例1 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
工作时间(月) 工作效率 工作总量(1)
甲队
乙队
等量关系:
甲队完成的工作总量+乙队完成的工作总量=“1”
设乙单独 完成这项工程需要x个月.
解:设乙单独 完成这项工程需要x个月.根据题意得
方程两边都乘以6x,得
解得 x=1.
检验:当x=1时,6x≠0.
所以,原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,而甲队单独施工需3个月才可以完成全部任务,所以乙队的施工速度快.
例2 某次列车平均提速v千米/时,用相同的时间,列车提速前行使s千米,提速后比提速前多行使50千米,提速前列车的平均速度为多少?
时间(时) 速度(千米/时) 路程(千米)
提速前
提速后
设提速前列车的平均速度为x千米/时.
s
v+x
S+50
x
等量关系:
提速前行驶时间=提速后行驶时间
解:设提速前列车的平均速度为x千米/时,根据题意得
解得
经检验:
x= 是原方程的解
答:提速前列车的速度为 千米/时.
列分式方程解应用题的一般步骤
1.审:审清题意,并设未知数
2.找:找出相等关系
3.列:列出方程
4.解:解这个分式方程;
5.验:既要检验根是否是所列分式方程的根,又要检验根是否符合题意;
6.写:写出答案.
当堂练习
1.某工程队需要在规定日期内完成.若甲队单独做正好按时完成;若乙队单独做,超过规定日期三天才能完成.现由甲、乙合作两天,余下工程由乙队单独做,恰好按期完成,问规定日期是多少天?
解;设规定日期是x天,根据题意,得:
方程两边同乘以x(x+3),得:
2(x+3)+x2=x(x+3)
解得: x=6
检验:x=6时x(x+3)≠0,x=6是原方程的解.
答:规定日期是6天.
2.一轮船往返于A、B两地之间,顺水比逆水快1小时到达.已知A、B两地相距80千米,水流速度是2千米/小时,求轮船在静水中的速度.
x=-18(不合题意,舍去),
解:设船在静水中的速度为x千米/小时,根据题意得
解得 x=±18.
检验得:x=18.
答:船在静水中的速度为18千米/小时.
方程两边同乘(x-2)(x+2)得
80x+160 -80x+160=x2 -4.
3. 某校师生到距学校15千米的景区游玩,一部分人骑自行车先走,过了40分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度.
解:设自行车的速度为x千米/时,那么汽车的速度是3x千米/时,依题意得:
解得
x=15.
经检验,x=15是原方程的根.
由x=15得3x=45.
答:自行车的速度是15千米/时,汽车的速度是45千米/时.
课堂小结
分式方程的应用
类型
行程问题、工程问题、数字问题、顺逆问题、买卖问题等
步骤
一审二设三找四列五解六验七写
习题9.3第5、6题
课后作业
