沪科版七年级下册数学 9.3.1分式方程及其解法 课件(共14张PPT)
文档属性
| 名称 | 沪科版七年级下册数学 9.3.1分式方程及其解法 课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 524.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-11 06:32:00 | ||
图片预览





文档简介
(共14张PPT)
分式方程及其解法
1、理解分式方程及增根的概念
2、掌握解简单的分式方程
3、了解分式方程产生增根的原因
4、掌握检验根的方法。
去分母,
去括号,
移项,
合并同类项,
系数化为1,
解:方程两边同乘以15,得
你能找出下列分式的最简公分母吗?
最简公分母(x+5)(x-5)
最简公分母(x-3)
最简公分母 1.25x
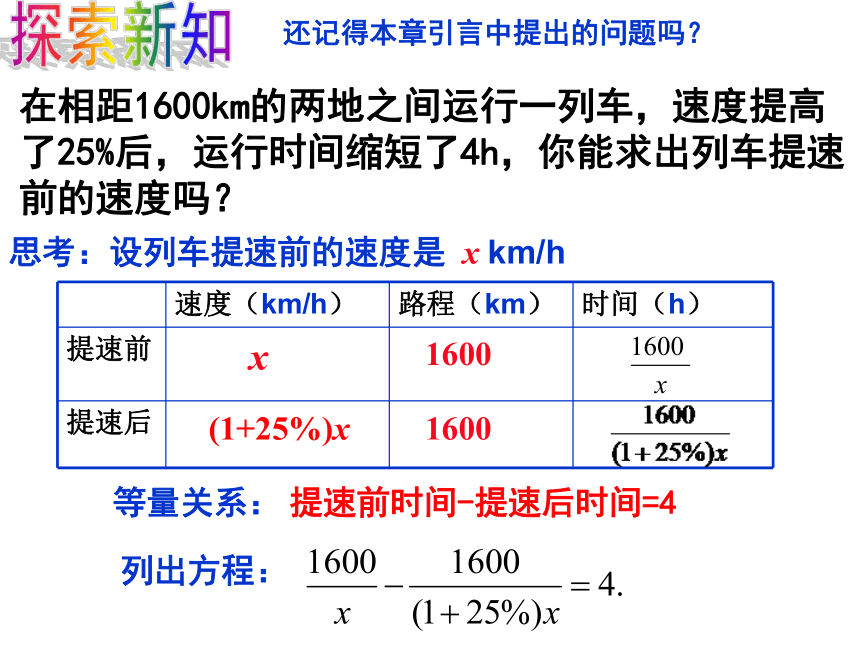
在相距1600km的两地之间运行一列车,速度提高了25%后,运行时间缩短了4h,你能求出列车提速前的速度吗?
速度(km/h) 路程(km) 时间(h)
提速前
提速后
x
1600
1600
思考:设列车提速前的速度是 x km/h
还记得本章引言中提出的问题吗?
(1+25%)x
等量关系:
列出方程:
提速前时间-提速后时间=4
该方程与前面学过的方程有什么不同?它有何特点?
分母中含有未知数
像这样,分母中含有未知数的方程叫做分式方程.
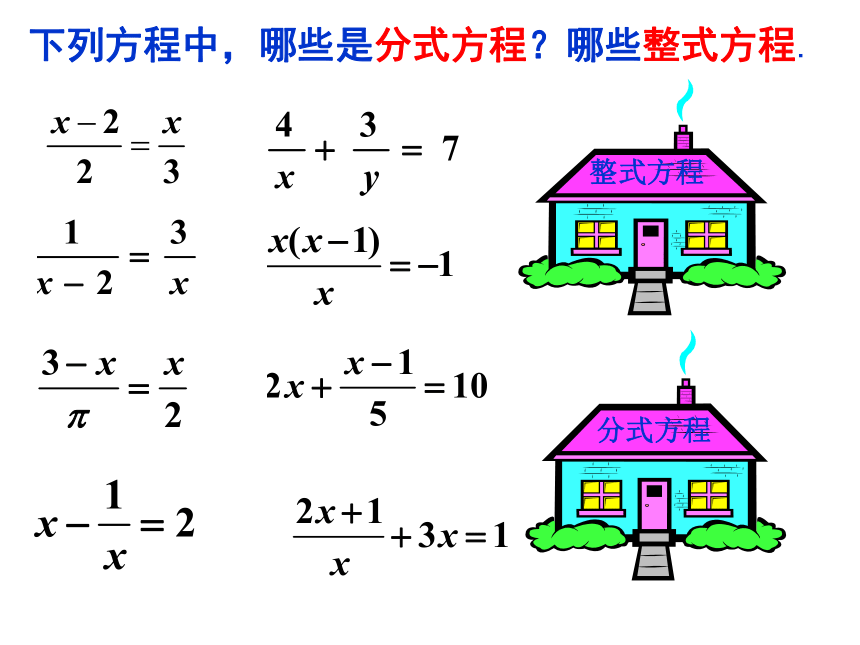
下列方程中,哪些是分式方程?哪些整式方程.
整式方程
分式方程
分式方程
整式方程
去分母
怎样解上面的分式方程呢?
两边同乘以
最简公分母
试一试:两边同乘以什么样
的整式,可以去掉分母呢?
解:方程两边同乘以1.25x,得
(1)请你解 方程,并把解
得的根代入原方程中检验,你发现了什么?
把x=3代入原方程检验时,分式的分母为0。分式无意义,所以x=3不是原方程的根,原方程无解.
解:
x=3是增根
使最简公分母值为零的根
方程两边同乘以(x-3)得
增根的定义
(2)出现增根的原因是什么?这给我们解分式方程有什么启示?
产生增根的原因:
分式方程两边同乘以一个0后,所得的根
是整式方程的根,而不是分式方程的根.
所以,解分式方程必须验根
使最简公分母值为零的根
例1 解方程:
分析:先找出方程中各分母的最简公分母是(x+3)(x-3)
解: 两边同乘以(x+3)(x-3),得
(x-1)(x-3)-2(x+3)(x-3)=-x(x+3) ,
x2-4x+3-2x2+18=-x2-3x
x=21
检验:当x=21时,(x+3)(x-3)≠0.
因而,原方程的根是x=21.
x2-3x-x+3-2(x2-9)=-x2-3x
-x=-21
-4x+3x=-3-18
分式方程
整式方程
解整式方程
检验
转化
作答
解分式方程的一般步骤
4、写出原方程的根.
一化二解三检验四写
1、方程两边都乘以最简公分母,化成整式方程
2、解这个整式方程.
3、检验:把整式方程的解代入最简公分母,
如果值不为0,就是原分式方程的解;如果值
为0,原分式方程无解.
1.练习
解方程:
(1)
(2)
补充拓展练习
1.什么是分式方程?怎样解分式方程?
2.解分式方程为什么一定要检验?
分式方程两边同乘以一个0后,所得的根
是整式方程的根,而不是分式方程的根.
所以,解分式方程必须验根
分式方程及其解法
1、理解分式方程及增根的概念
2、掌握解简单的分式方程
3、了解分式方程产生增根的原因
4、掌握检验根的方法。
去分母,
去括号,
移项,
合并同类项,
系数化为1,
解:方程两边同乘以15,得
你能找出下列分式的最简公分母吗?
最简公分母(x+5)(x-5)
最简公分母(x-3)
最简公分母 1.25x
在相距1600km的两地之间运行一列车,速度提高了25%后,运行时间缩短了4h,你能求出列车提速前的速度吗?
速度(km/h) 路程(km) 时间(h)
提速前
提速后
x
1600
1600
思考:设列车提速前的速度是 x km/h
还记得本章引言中提出的问题吗?
(1+25%)x
等量关系:
列出方程:
提速前时间-提速后时间=4
该方程与前面学过的方程有什么不同?它有何特点?
分母中含有未知数
像这样,分母中含有未知数的方程叫做分式方程.
下列方程中,哪些是分式方程?哪些整式方程.
整式方程
分式方程
分式方程
整式方程
去分母
怎样解上面的分式方程呢?
两边同乘以
最简公分母
试一试:两边同乘以什么样
的整式,可以去掉分母呢?
解:方程两边同乘以1.25x,得
(1)请你解 方程,并把解
得的根代入原方程中检验,你发现了什么?
把x=3代入原方程检验时,分式的分母为0。分式无意义,所以x=3不是原方程的根,原方程无解.
解:
x=3是增根
使最简公分母值为零的根
方程两边同乘以(x-3)得
增根的定义
(2)出现增根的原因是什么?这给我们解分式方程有什么启示?
产生增根的原因:
分式方程两边同乘以一个0后,所得的根
是整式方程的根,而不是分式方程的根.
所以,解分式方程必须验根
使最简公分母值为零的根
例1 解方程:
分析:先找出方程中各分母的最简公分母是(x+3)(x-3)
解: 两边同乘以(x+3)(x-3),得
(x-1)(x-3)-2(x+3)(x-3)=-x(x+3) ,
x2-4x+3-2x2+18=-x2-3x
x=21
检验:当x=21时,(x+3)(x-3)≠0.
因而,原方程的根是x=21.
x2-3x-x+3-2(x2-9)=-x2-3x
-x=-21
-4x+3x=-3-18
分式方程
整式方程
解整式方程
检验
转化
作答
解分式方程的一般步骤
4、写出原方程的根.
一化二解三检验四写
1、方程两边都乘以最简公分母,化成整式方程
2、解这个整式方程.
3、检验:把整式方程的解代入最简公分母,
如果值不为0,就是原分式方程的解;如果值
为0,原分式方程无解.
1.练习
解方程:
(1)
(2)
补充拓展练习
1.什么是分式方程?怎样解分式方程?
2.解分式方程为什么一定要检验?
分式方程两边同乘以一个0后,所得的根
是整式方程的根,而不是分式方程的根.
所以,解分式方程必须验根
