三角函数的应用[下学期]
图片预览




文档简介
课件18张PPT。三角函数
S= Asin(ω t + ψ )的应用
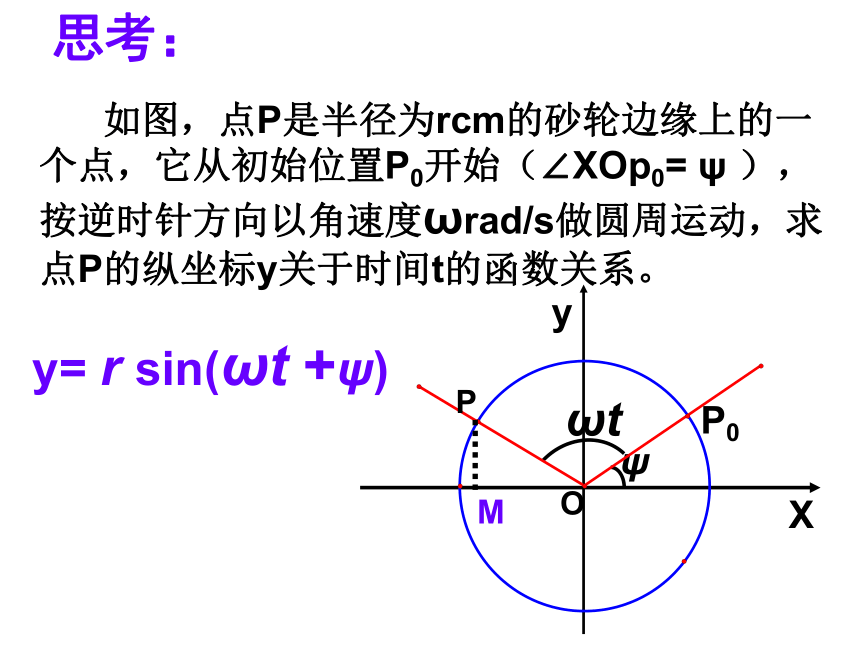
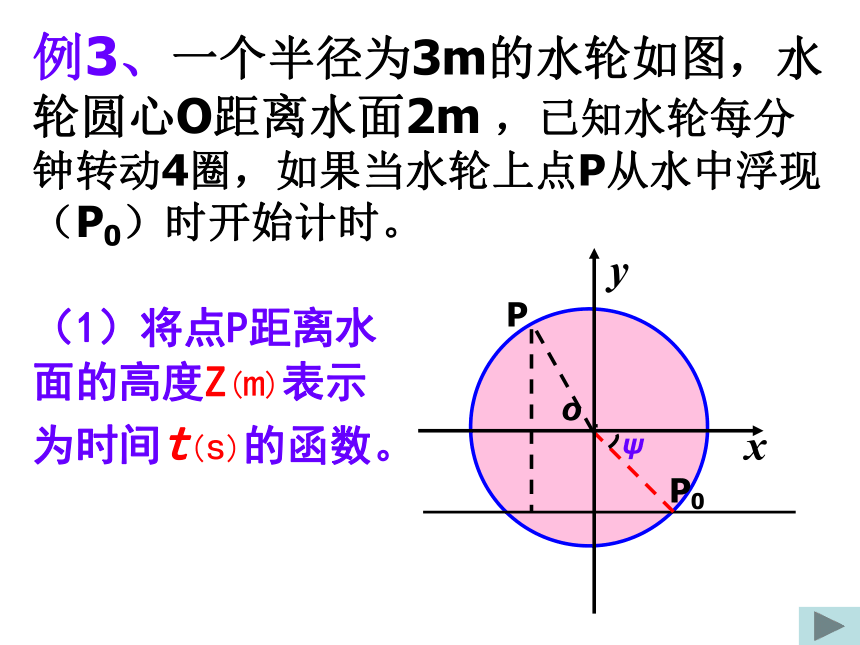
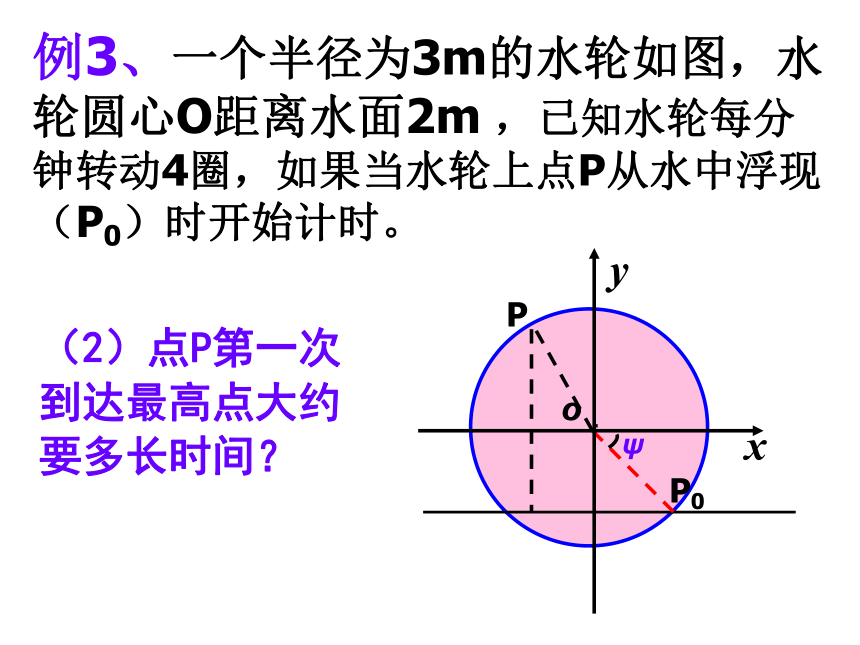
(2)思考: 如图,点P是半径为rcm的砂轮边缘上的一个点,它从初始位置P0开始(∠XOp0= ψ ),按逆时针方向以角速度ωrad/s做圆周运动,求点P的纵坐标y关于时间t的函数关系。P0y= r sin(ωt +ψ)例3、一个半径为3m的水轮如图,水轮圆心O距离水面2m ,已知水轮每分钟转动4圈,如果当水轮上点P从水中浮现(P0)时开始计时。(1)将点P距离水面的高度Z(m)表示为时间t(s)的函数。O .例3、一个半径为3m的水轮如图,水轮圆心O距离水面2m ,已知水轮每分钟转动4圈,如果当水轮上点P从水中浮现(P0)时开始计时。(2)点P第一次到达最高点大约要多长时间?O .练 习回顾作业题 11例4、若某地温度T是一天为周期的函数,此函数可用y= Asin(ωt +ψ)+b近似表示,当t =14时达到最高温度15℃,当t =2时达到最低温度3 ℃,
求温度T(℃)和t之间的函数关系式。练习: P45 2(评价手册 P32 4) 海水受日月的引力,在一定的时候发生涨落的现象叫潮汐,一般的早潮叫潮,晚潮叫汐。
通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋。小 常 识船的吃水深度a:海底水面船的安全间隙 b:例5、下面是某港口在某季节每天几个时刻的水深。(1)选用一个三角函数来近似描述这个港口的水深与时间的函数关系,并给出在整点时的水深的近似数值。解:(1) 设y= Asinωt + k,由题意可得:A=(7.5-2.5)/2=2.5, k=5, T=12,ω=y= 2.5sin t + 5所以:y= 2.5sin t + 5各整点时的水深为:t=1,5,13,17时,水深6.3mt=2,4,14,16时,水深7.2mt=7,11,19,23时,水深3.7mt=8,10,20,22时,水深2.8m例5、下面是某港口在某季节每天几个时刻的水深。(2)一条货船的吃水深度为4m,安全条例规定至少要有1.5m的安全间隙,该船何时能进港?在港口能呆多久?(2)一条货船的吃水深度为4m,安全条例规定至少要有1.5m的安全间隙,该船何时能进港?在港口能呆多久?2.5sin t + 5 ≥5.5解:(2) 由题意须 y≥ 4+1.5sin t ≥0.2由图象可得 0.4≤t ≤5.6 或 12.4≤t ≤17.6 所以船在0:24至5:36和12:24至17:36 进港, 能呆5.2小时 例5、下面是某港口在某季节每天几个时刻的水深。(3)若船的吃水深度为4m,安全间隙为1.5m,该船在2:00开始卸货,吃水深度以0.3m/时的速度减少,那么该船在什么时间必须停止卸货,离港开往深水处?(3)若船的吃水深度为4m,安全间隙为1.5m,该船在2:00开始卸货,吃水深度以0.3m/时的速度减少,那么该船在什么时间必须停止卸货,离港开往深水处?解:(3) 由题意须 y≥ 吃水深度 +1.5吃水深度= 4- 0.3(t-2)(2≤t ≤24)sin t ≥0.44-0.12t由图象可得 t =6.7 即6:42时必须停止卸货。练习:
P45 3 三角函数应用题的解题步骤可以用下面的框图表示:数学模型的解实际应用问题数学模型海底水面
求温度T(℃)和t之间的函数关系式。练习: P45 2(评价手册 P32 4) 海水受日月的引力,在一定的时候发生涨落的现象叫潮汐,一般的早潮叫潮,晚潮叫汐。
通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋。小 常 识船的吃水深度a:海底水面船的安全间隙 b:例5、下面是某港口在某季节每天几个时刻的水深。(1)选用一个三角函数来近似描述这个港口的水深与时间的函数关系,并给出在整点时的水深的近似数值。解:(1) 设y= Asinωt + k,由题意可得:A=(7.5-2.5)/2=2.5, k=5, T=12,ω=y= 2.5sin t + 5所以:y= 2.5sin t + 5各整点时的水深为:t=1,5,13,17时,水深6.3mt=2,4,14,16时,水深7.2mt=7,11,19,23时,水深3.7mt=8,10,20,22时,水深2.8m例5、下面是某港口在某季节每天几个时刻的水深。(2)一条货船的吃水深度为4m,安全条例规定至少要有1.5m的安全间隙,该船何时能进港?在港口能呆多久?(2)一条货船的吃水深度为4m,安全条例规定至少要有1.5m的安全间隙,该船何时能进港?在港口能呆多久?2.5sin t + 5 ≥5.5解:(2) 由题意须 y≥ 4+1.5sin t ≥0.2由图象可得 0.4≤t ≤5.6 或 12.4≤t ≤17.6 所以船在0:24至5:36和12:24至17:36 进港, 能呆5.2小时 例5、下面是某港口在某季节每天几个时刻的水深。(3)若船的吃水深度为4m,安全间隙为1.5m,该船在2:00开始卸货,吃水深度以0.3m/时的速度减少,那么该船在什么时间必须停止卸货,离港开往深水处?(3)若船的吃水深度为4m,安全间隙为1.5m,该船在2:00开始卸货,吃水深度以0.3m/时的速度减少,那么该船在什么时间必须停止卸货,离港开往深水处?解:(3) 由题意须 y≥ 吃水深度 +1.5吃水深度= 4- 0.3(t-2)(2≤t ≤24)sin t ≥0.44-0.12t由图象可得 t =6.7 即6:42时必须停止卸货。练习:
P45 3 三角函数应用题的解题步骤可以用下面的框图表示:数学模型的解实际应用问题数学模型海底水面
