4.8三角函数小结与复习[上学期]
图片预览




文档简介
(共17张PPT)
第四章 三角函数
小结与复习
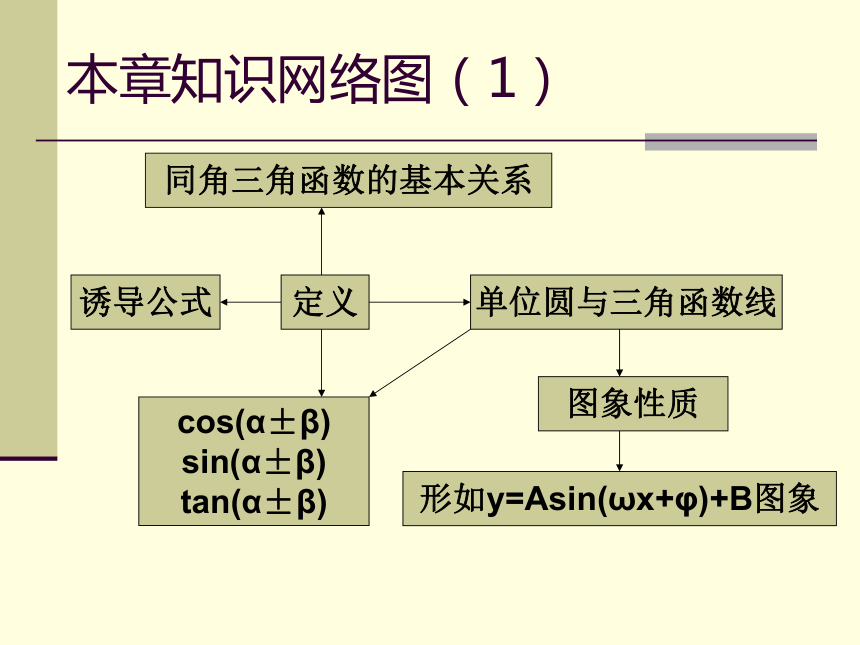
本章知识网络图(1)
诱导公式
定义
单位圆与三角函数线
图象性质
同角三角函数的基本关系
形如y=Asin(ωx+φ)+B图象
cos(α±β)
sin(α±β)
tan(α±β)
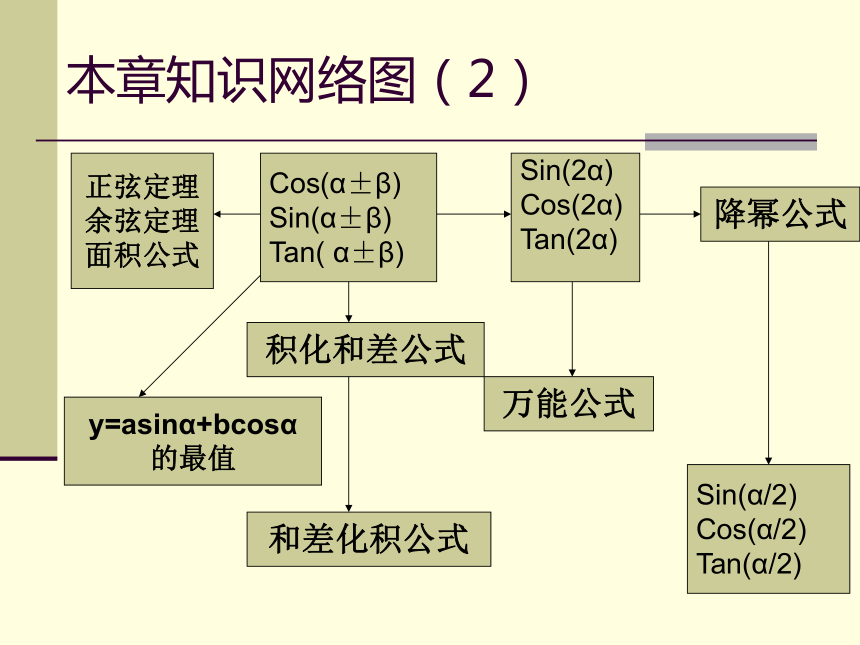
本章知识网络图(2)
Cos(α±β)
Sin(α±β)
Tan( α±β)
Sin(2α)
Cos(2α)
Tan(2α)
万能公式
降幂公式
Sin(α/2)
Cos(α/2)
Tan(α/2)
积化和差公式
和差化积公式
正弦定理
余弦定理
面积公式
y=asinα+bcosα
的最值
内容提要
任意角的概念
正角、负角
角度制
弧度制
弧长公式
任意角的三角函数
内容提要
同一个角的正弦、余弦、正切、余切函数
的三个关系式:
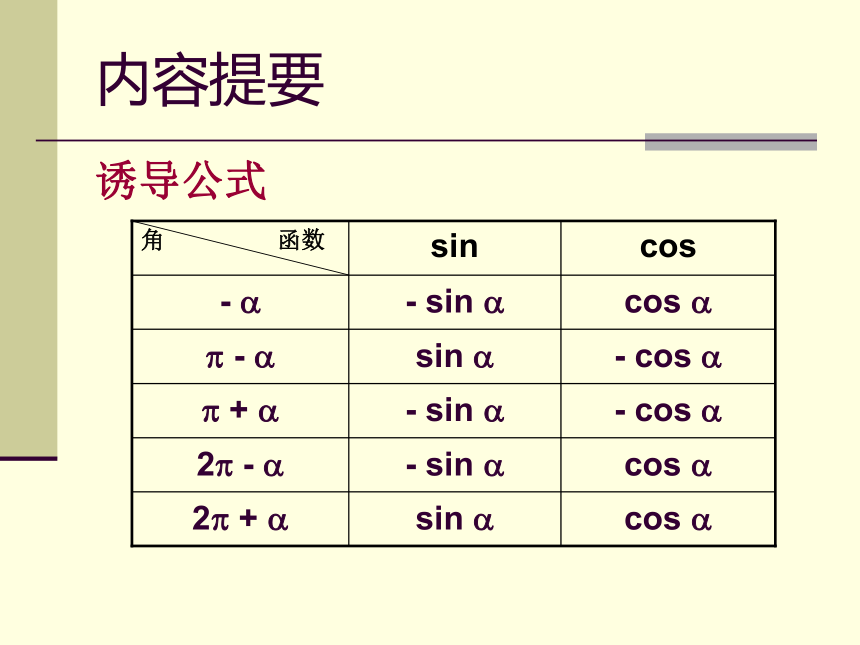
内容提要
诱导公式
cos
- sin
2 -
- cos
- sin
+
- cos
sin
-
cos
- sin
-
sin
2 +
cos
cos
sin
角 函数
内容提要
和(差)角公式
内容提要
倍角公式
内容提要
周期为
周期为2
周期为2
周期性
R
函数无最大值、
最小值
[-1,1]
最大值为1
最小值为-1
[-1,1]
最大值为1
最小值为-1
值域
{x|x ( /2)+k ,k Z}
R
R
定义域
正切函数
余弦函数
正弦函数
函数
正弦、余弦、正切函数的主要性质
内容提要
在[k -( /2),
k +( /2)]内
都是增函数
(k Z)
在[(2k-1) ,
2k 上都是
增函数
在[2k ,
(2k +1) ]上都是减函数
在[2k -( /2),
2k +( /2)]上
都是增函数
在[2k +( /2),
2k +(3 /2)]上都是减函数
单调性
奇函数
偶函数
奇函数
奇偶性
正切函数
余弦函数
正弦函数
函数
正弦、余弦、正切函数的主要性质(续)
内容提要
函数图像变换
y=f(x)图象
y=f(x)+b图象
y=f(x+φ)图象
y=Af(x)图象
y=f(ωx)图象
向上(b>0)或向下(b<0)移︱b︱单位
向左(φ>0)或向右(φ<0)移︱φ︱单位
点的横坐标变为原来的1/ω倍
纵坐标不变
点的纵坐标变为原来的A倍
横坐标不变
常见问题
正弦、余弦和正切函数都是周期函数。
正弦、余弦函数的周期为2 ;
正切函数的周期为 .
在几何画图中,运用将图形平行移动的方法。
根据画图的需要,将已知图形上点的横、纵坐标
进行伸长或缩短。
常见问题
把未知划归为已知
把特殊化划归为一般
等价划归
划归思想
例题
化简
其中k Z.
分析:原式
这启发我们运用余弦的和(差)角公式.
例题
解法1:原式
例题
解法2:由 可知
所以 原式
第四章 三角函数
小结与复习
本章知识网络图(1)
诱导公式
定义
单位圆与三角函数线
图象性质
同角三角函数的基本关系
形如y=Asin(ωx+φ)+B图象
cos(α±β)
sin(α±β)
tan(α±β)
本章知识网络图(2)
Cos(α±β)
Sin(α±β)
Tan( α±β)
Sin(2α)
Cos(2α)
Tan(2α)
万能公式
降幂公式
Sin(α/2)
Cos(α/2)
Tan(α/2)
积化和差公式
和差化积公式
正弦定理
余弦定理
面积公式
y=asinα+bcosα
的最值
内容提要
任意角的概念
正角、负角
角度制
弧度制
弧长公式
任意角的三角函数
内容提要
同一个角的正弦、余弦、正切、余切函数
的三个关系式:
内容提要
诱导公式
cos
- sin
2 -
- cos
- sin
+
- cos
sin
-
cos
- sin
-
sin
2 +
cos
cos
sin
角 函数
内容提要
和(差)角公式
内容提要
倍角公式
内容提要
周期为
周期为2
周期为2
周期性
R
函数无最大值、
最小值
[-1,1]
最大值为1
最小值为-1
[-1,1]
最大值为1
最小值为-1
值域
{x|x ( /2)+k ,k Z}
R
R
定义域
正切函数
余弦函数
正弦函数
函数
正弦、余弦、正切函数的主要性质
内容提要
在[k -( /2),
k +( /2)]内
都是增函数
(k Z)
在[(2k-1) ,
2k 上都是
增函数
在[2k ,
(2k +1) ]上都是减函数
在[2k -( /2),
2k +( /2)]上
都是增函数
在[2k +( /2),
2k +(3 /2)]上都是减函数
单调性
奇函数
偶函数
奇函数
奇偶性
正切函数
余弦函数
正弦函数
函数
正弦、余弦、正切函数的主要性质(续)
内容提要
函数图像变换
y=f(x)图象
y=f(x)+b图象
y=f(x+φ)图象
y=Af(x)图象
y=f(ωx)图象
向上(b>0)或向下(b<0)移︱b︱单位
向左(φ>0)或向右(φ<0)移︱φ︱单位
点的横坐标变为原来的1/ω倍
纵坐标不变
点的纵坐标变为原来的A倍
横坐标不变
常见问题
正弦、余弦和正切函数都是周期函数。
正弦、余弦函数的周期为2 ;
正切函数的周期为 .
在几何画图中,运用将图形平行移动的方法。
根据画图的需要,将已知图形上点的横、纵坐标
进行伸长或缩短。
常见问题
把未知划归为已知
把特殊化划归为一般
等价划归
划归思想
例题
化简
其中k Z.
分析:原式
这启发我们运用余弦的和(差)角公式.
例题
解法1:原式
例题
解法2:由 可知
所以 原式
